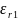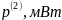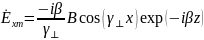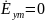Курсовые / Эмпив курсач 2 часть

Государственное образовательное учреждение высшего профессионального образования

Московский технический университет связи и информатики

Курсовая работа

по дисциплине:

«Электромагнитные поля и волны»

Часть 2. «Основные уравнения электродинамики»

Задача № 2- 1

Выполнил:

студент группы БСУ1301

Ежов А.А.

Москва 2015г

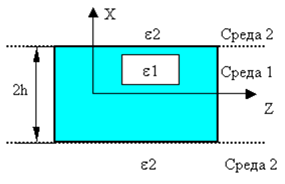
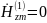
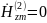
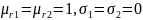
		2h,мкм	f,ТГц
3,5	1,9	1,4	280	0,5	-

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов 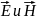в среде 1 и 2.

Найдём комплексные амплитуды вектора

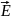
1 среда	2 среда

Из 2 уравнения Максвелла следует:

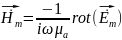
Спроектируем полученное равенство на оси координат

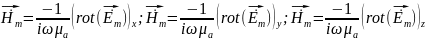
Определим проекции

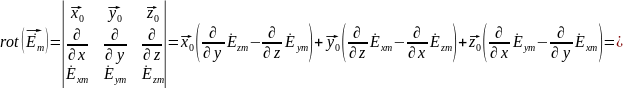
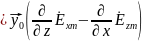
Комплексная амплитуда

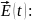
1 среда

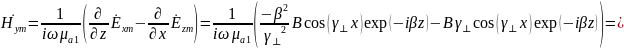
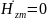
2 среда

2. На основе граничных условий и связи поперечных волновых чисел с коэффициентом распространения составить уравнения для определения поперечных волновых чисел α⊥ и γ⊥ . Решить полученные уравнения относительно α⊥ и γ⊥.

Запишем уравнение Гельмгольца:

Подставим наши функции:

Среда 1	Среда 2

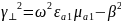
Сложим полученные выражения:

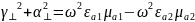
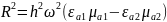
Используем граничные условия:

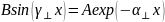
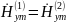
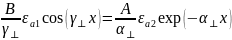
Разделим уравнения:

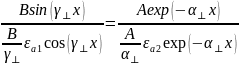
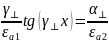
Помножим на h:

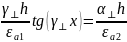
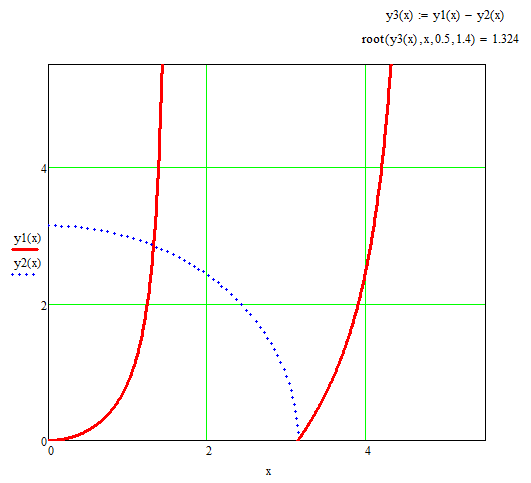
Построим графики:

Точка пересечения этих графиков ( ):

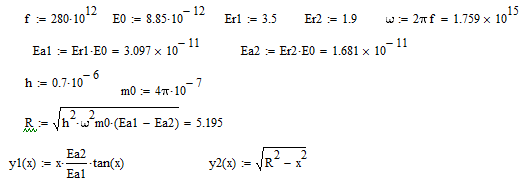
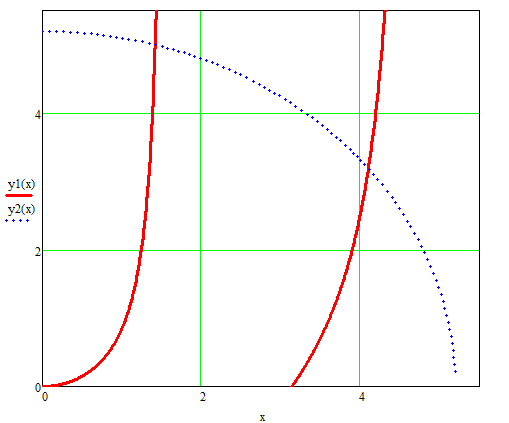
3. Определить обеспечивается ли одноволновый (одномодовый) режим работы световода на частоте f. Если условия одноволновости не выполняется, определить максимальную толщину световода для его выполнения:

По графику видно, что условия одноволновости не выполняются.

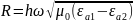
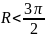
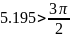
Следовательно, найдем максимальную толщину при которой будет выполнятся одноволновый режим:

Найдем нули функции. Нас интересует второй ноль, который находится на интервале от 2 до 4. С помощью MathCad найдем значения x при которой y1(x)=0

Следовательно для обеспечения одноволнового режима нам нужна взять R<=3.142

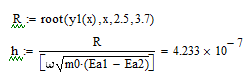
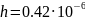
Точка пересечения

4) Определить параметры γ⊥, α⊥, β, Vф, а также, используя заданную величину 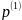, определить постоянные А и В для низшего типа волны.

Так как

То

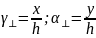
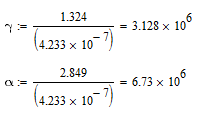
Среда 1	Среда 2

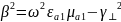
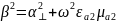
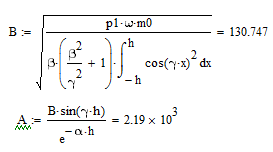
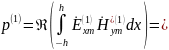
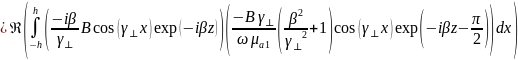
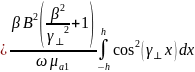
Используя граничные условия найдем А:

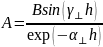
5) Рассчитать и построить зависимости амплитуд всех составляющих полей от координаты Х для низшего типа волны в средах 1 и 2.

Для построения графиков необходимо перейти от комплексных значений к реальным

Для удобства примем z=1

Построим график зависимости составляющей

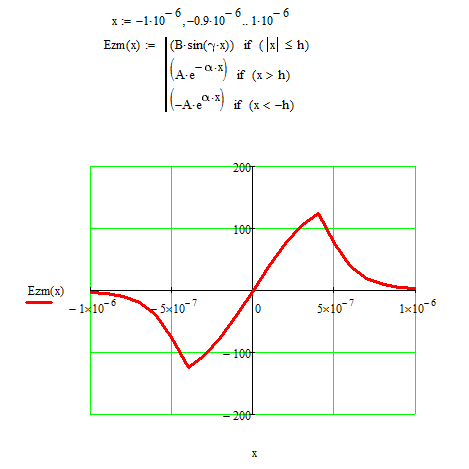
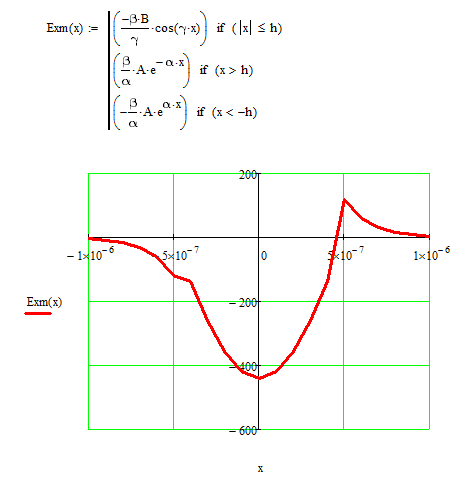
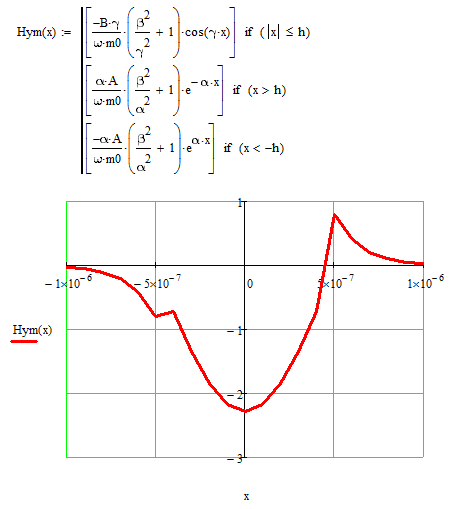
Из графиков видно, что вне пластины поле убывает по экспоненте.

6) Определить процентное соотношение мощностей Р⁽²⁾ и Р⁽¹⁾, проходящих через поперечное сечение сред 1 и 2 для низшего типа волны

7) Заменить плоскийсветовод волоконным диаметром 2h с параметрами , , окруженным защитной оболочкой с параметрами ,

Определить, обеспечивается ли при заданных параметрах световода и частоте fодноволновый (одномодовый) режим работы световода на волне основного (низшего) типа НЕ11, для которой кр = 

Для того, чтобы волна распространялась в направляющей системе необходимо, чтобы

Длина волны в вакууме:

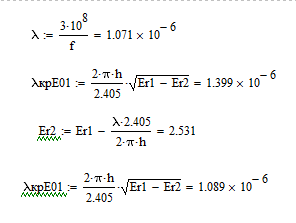
Т.е. если

условие одноволновости не выполняется

условие одноволновости определяется

Рассчитаем критическую длину волны:

В нашем случае - условие одноволновости не выполняется

Если условие одноволновости не выполняется, определить минимальную необходимую диэлектрическую проницаемость защитной оболочки световода для его выполнения

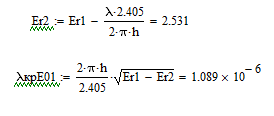
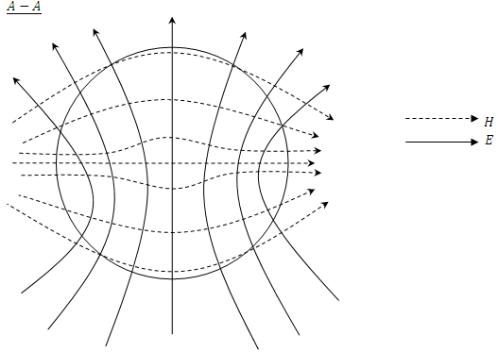
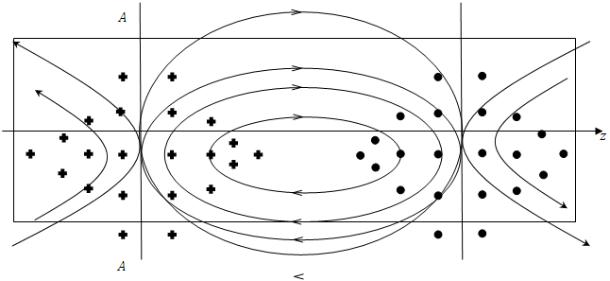
8) Изобразить структуру поля основного типа волны НЕ11 в поперечном сечении волновода