Добавил:

Svyazist_Ot_Boga Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Основы Теории Электромагнитных Полей и Волн

Файл:

Курсовые / Отчет_ЭМПиВ_к.р.1-1(3 курс_1 семестр)

.pdf

Скачиваний:

Добавлен:

06.08.2022

Размер:

172.67 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Государственное образовательное учреждение высшего профессионального образования

Московский технический университет связи и информатики

Кафедра технической электродинамики и антенн

Курсовая работа

по дисциплине:

«Электромагнитные поля и волны»

Часть 1. «Основные уравнения электродинамики»

Вариант №1

Выполнил:

студент группы СС0902

Ежов П.А.

Проверил:

доцент кафедры ТЭДиА

Гайнутдинов Т.А.

Москва 2011г

В соответствии с заданием исследовать основные свойства монохроматического электромагнитного поля, существующего в системе, изображенной на рисунке (прямоугольном волноводе).

Волновод заполнен однородной изотропной средой с параметрами εr , μr , σ = 0 . Стенки волновода являются идеально проводящими.

Известны выражения для составляющих векторов поля:

&	πx			&
Hzm = H 0	×cos	×exp(-iβz) , Ezm = 0
	a
Исходные данные:
λкр = 2a

H0, А/м	εr		μr		a, мм	b, мм	F1, МГц	f2, МГц

10	1		1		30	20	3.75	7.5

1.Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов E и H .

Комплексные амплитуды составляющих вектора H :

= grad

×(

iβ

)

H zm

0π

πx

dH zm

grad H zm

= -

sin

× x0

H m

= grad H zm

+ H

iβπH 0

sin

πx

−iβz

H xm

aγ

= 0

H ym

= H

πx

−iβz

×cos

Из уравнения Максвелла найдем комплексные амплитуды вектора E :

rotH m = iωε a Em

rotH m

iωε a

rotH

= x

−

+ y

−

+ z

−

H xm

H ym

H zm

πH 0

πx

−iβz

H 0π

πx

H 0π

πx

−iβz

= y

sin

= y

sin

aγ

H 0π

πx

−iβz

= y

γ 2 iaωε

sin

= 0

Exm

H 0π

πx

−iβz

E ym

sin

iaωε a

= 0

Ezm

2.Определить диапазон частот, в котором рассматриваемое поле представляет собой волну,

бегущую вдоль оси z. Условие бегущей волны: f > fкр или λ < λкр .

β =	2 π		λ 2
		1-
	λ
			2a

Откуда видно, что β – действительное при λ £ 2a

λкр = 2a = 0.06 м

т.к. ε r = 1 и μr =1, то Ccp = c = 3 ×108 м/с

fкр = Ccp = 5 ×109 Гц

λкр

Следовательно: рассматриваемое поле – бегущая волна при f ³ 5 ×109 Гц

3.Записать выражения для мгновенных значений всех составляющих векторов полей.

Рассчитать и построить графики зависимостей мгновенных значений составляющих полей

от координаты z (при x=a/3, y=b/3) в два момента времени: t1=0 и t2=T/4 в интервале

0 ≤ z ≤ 2Λ , где Λ - длина волны в волноводе на частоте f2. Задание этого пункта выполняется для двух частот: f1 и f2.

а) Мгновенные значения всех составляющих векторов E и H для

> fкр ;

Ex (t) = 0

πx

iω2t

−iβ2 z

iω2t

×e

sin

E y (t) = Re{Eym

}= Re

iaω2ε a

πx

sin

cos ω2t - β2 z -

aω2ε a

Ez (t) = 0

iω2t

πx

−iβ2 z

×e

iβ2 H 0π

iω2t

(t) = Re{H

}= Re

2 a

sin

πH

πx

t - β

2 a

sin

cos

H y (t) = 0

H z (t) =

iωt

0 ×cos

πx

−iβ2 z

iω2t

H 0 ×cos

πx

β2 z)

Re{H zm ×e

}= Re H

cos(ω2t -

t=0

Ex (t) = 0

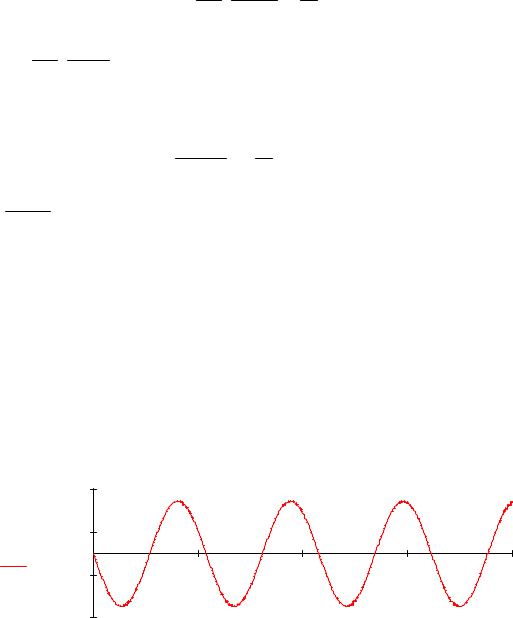
E y (t) = 4.89 ×103 ×cos(-117.08 × z -1.57)

Ez (t) = 0

6×103

2×103

Ey(t , z)

3 0

0.05

0.1

0.15

0.2

− 2×10

− 6×103

H x (t) = 9.68 ×cos(-117.08 × z +1.57)
H y (t) = 0
H z (t) = 5 ×cos(-117.08 × z)
	10
Hx(t , z)	5
Hx(t , z)
Hz( t , z)	0	0.05	0.1	0.15	0.2
	− 5
− 10
			z
2)	t=T/4

Ex (t) = 0
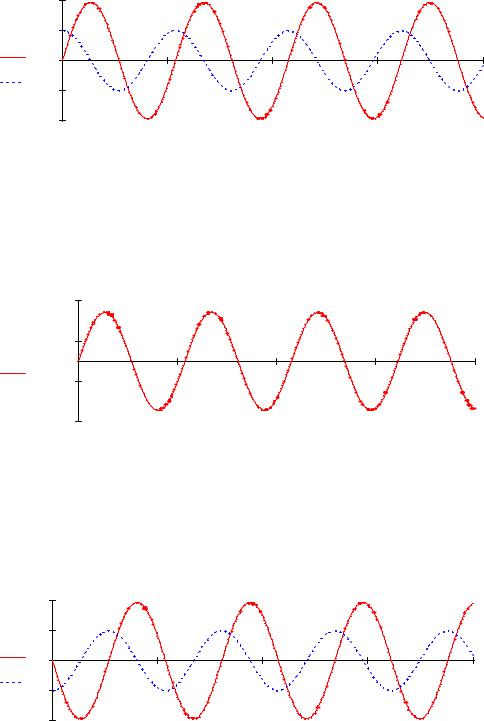
Ey (t) = 4.89 ×103 ×cos(-117.08 × z)
Ez (t) = 0
	6×103
	2×103
Ey(z)	− 2×103 0	0.05	0.1	0.15	0.2
	− 2×103 0	0.05	0.1	0.15	0.2
	− 6×103
			z
H x (t) = 9.68 ×cos(-117.08 × z + π )
H y (t) = 0
H z (t) = 5 ×cos(-117.08 × z + π )
		2
	10
	5
Hx(z)
Hz( z)	0	0.05	0.1	0.15	0.2
	− 5
− 10

б) Мгновенные значения всех составляющих векторов E и H для f1 < fкр ;

Представим β1 = −iα

, где α =

2π

-1

Ex (t) = 0

πx

iω1t

−αz

iω1t

E y (t) =

Re{E ym

× e

}= Re

1 -

2 iω ε a

sin

πx

= 1

−αz sin

cos(ω t -

)

2 ω ε

Ez (t) = 0

iω1t

πx

−az

iω1t

απH 0

πx

−az

απH 0

H x (t) = Re{H xm × e

}= Re

sin

cosω1t × e

2 a

H y (t) = 0

iω1t

πx

−αz

iω1t

H 0 e

−αz

× cos

πx

H z (t) = Re{H zm × e

}= Re H 0 × cos

cosω1t

t=0

Ex (t) = 0

E y (t) = 1.15 ×10−13 × cos e−69.27 z

Ez (t) = 0

4×10−15

3×10−15

Ey(z) 2×10−15

1×10−15

0.05

0.1

0.15

0.2

H x (t) = 5.73 × e−69.27 z H y (t) = 0

H z (t) = 5 × e69.27 z

	0.15
Hx(z)	0.1
Hz( z)	0.05
	0.05
	0	0.05	0.1	0.15	0.2
			z
2) t=T/4

Ex (t) = 0
E y (t) = 1.73 ×103 × cos e−69.27 z
Ez (t) = 0
50
40
30
Ey(z)
20
10
0	0.05	0.1	0.15	0.2
		z
H x (t) = 4.05 × e −69.27 z
H y (t) = 0
H z (t) = 3.54 × e69.27 z
0.1
0.08
Hx(z)0.06
Hz (z)0.04
0.02
0	0.05	0.1	0.15	0.2
		z

4. Проверить выполнение граничных условий на стенках волновода (при х=0; а и у=0; b).

Граничные условия для касательных составляющих вектора E (Eτ ) и нормальной составляющей

вектора H (H n )на стенках волновода:

При x = 0:

x=0 = 0

E ym

x=0 = 0

Ezm

x=0 =

H xm

H 0

πx

−iβz

= 0

E ym

x=0

iaωε a

sin

x=0

= 0

Ezm

x=0

iβπH 0

πx

sin

−iβz

= 0

H xm

x =0

aγ

x=0

При x = а:

x=0 = 0

E ym

x=0 = 0

Ezm

x=0 =

H xm

H 0

πx

−iβz

= 0

E ym

x=0

iaωε a

sin

x=a

= 0

Ezm

x=0

iβπH 0

πx

sin

−iβz

= 0

H xm

x =0

aγ

x=a

При y = 0:

&			y =0	= 0
Exm
&			y =0	= 0

Ezm
&			y =0 = 0

H ym
&				= 0

Exm		y =0
				= 0
&
Ezm	y =0
				= 0
&
H ym			y =0

При y = b:
&		y =0		= 0

Exm
&	y =0			= 0

Ezm
&			y =0 = 0

H ym
&				= 0

Exm		y =0
				= 0
&
Ezm	y =0
				= 0
&
H ym			y =0

1 / 21 2 > Следующая >>>

Соседние файлы в папке Курсовые

#
06.08.202229.55 Кб11kursovaya_po_empiv.docx
#
06.08.2022263.42 Кб57курсовая 2.xmcd
#
06.08.20221.2 Mб42Курсовая работа по ЭМПиВ ч1 8 вариант.docx
#
06.08.2022466.18 Кб38Курсовая работа по ЭМПиВ ч2 8 вариант.docx
#
06.08.2022655.24 Кб41Курсовая1.xmcd
#
06.08.2022172.67 Кб40Отчет_ЭМПиВ_к.р.1-1(3 курс_1 семестр).pdf
#
06.08.2022898.19 Кб42Эмпив курсач 2 часть.docx