
Курсовые / Курсовая работа по ЭМПиВ ч2 8 вариант
.docxФедеральное Агентство Связи Федеральное Государственное Бюджетное Образовательное Учреждение Высшего Образования Ордена Трудового Красного знамени «Московский технический университет связи и информатики»
Кафедра технической электродинамики и антенн
Курсовая работа по дисциплине
«Электромагнитные поля и волны»
«Электромагнитные волны в световодах»
Бригада №8
Вариант № 1
Выполнил: ст. гр. БПЗ1802 Аркадьев Илья Дмитриевич Проверил:
Гайнутдинов Тимур Аншарович
Москва 2020
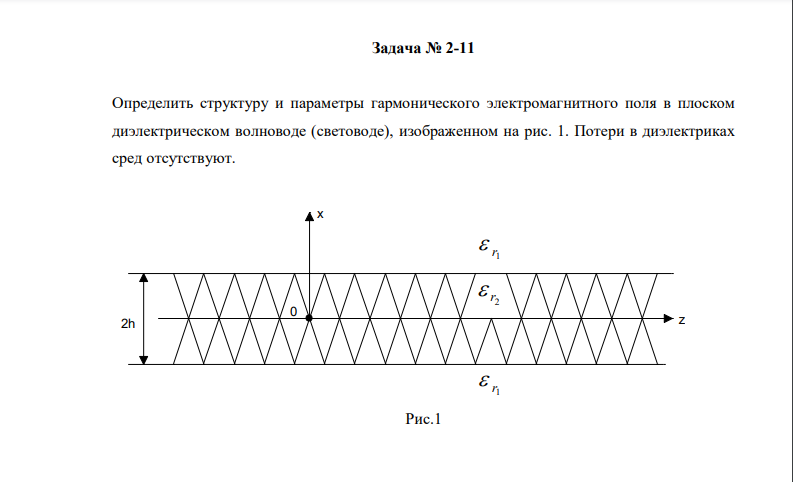

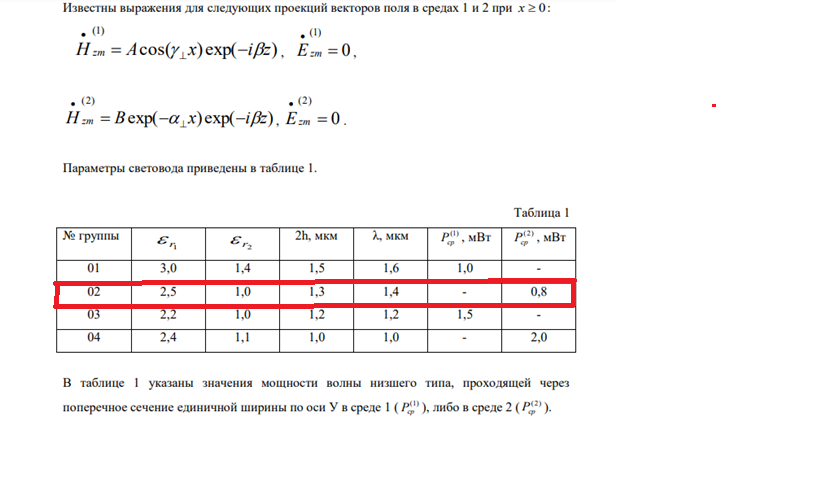


Выполнение
Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов
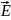 и
и
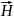 в средах 1 и 2
в средах 1 и 2
Для получения составляющих вектора , воспользуемся формулой второго уравнения Максвелла в комплексной форме

Расчет для 1-ой среды:

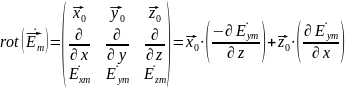
Возьмем частные производные:
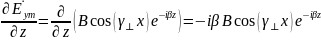
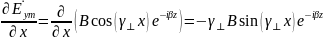
Получим следующие комплексные амплитуды:
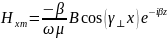
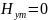
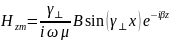
Расчет для 2-ой среды:
Возьмем частные производные:

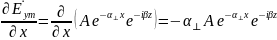
Получим следующие комплексные амплитуды:
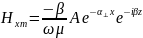
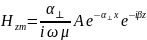
2.
На
основе граничных условий и связи
поперечных волновых чисел с коэффициентом
распространения
составить уравнения для определения
поперечных волновых чисел
 и
.
Решить полученные уравнения (например,
графически) относительно
и
.
и
.
Решить полученные уравнения (например,
графически) относительно
и
.
Система уравнений для граничных условий:
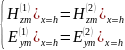
Подставим выражения, рассчитанные ранее в п.1:
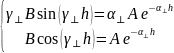
Выразим B из первого уравнения и подставим во второе уравнение:
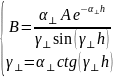
Применим
уравнение Гельмгольца к
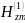 и
и
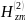 :
:

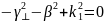
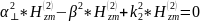
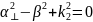
Получаем систему уравнений:
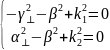
Сложим уравнения и окончательно получим:

Домножим уравнения на h:

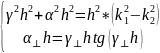
Выполним замену переменных:


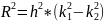
Тогда окончательно получим:
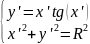
Решим полученные уравнения графически:
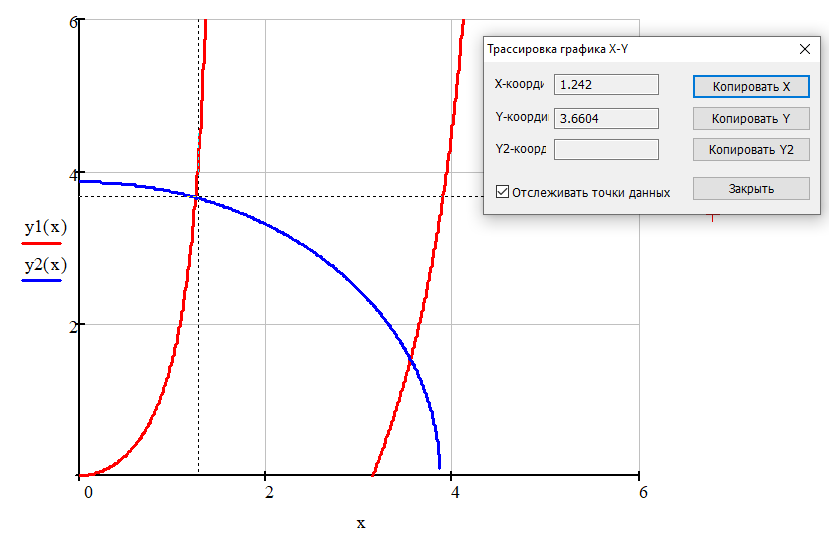
Точки пересечения графиков:
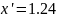

В
результате решения уравнений, найдем
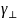 и
и
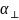 :
:

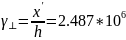
Определить, обеспечивается ли одноволновый (одномодовый) режим работы световода на частоте
 .
Если условие одномодовости не выполняется,
определить максимальную толщину
световода для его выполнения.
.
Если условие одномодовости не выполняется,
определить максимальную толщину
световода для его выполнения.
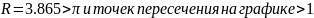 ,
следовательно, условие одноволновой
передачи не выполняется
,
следовательно, условие одноволновой
передачи не выполняется
Определим максимальную толщину световода для выполнения условия одномодовости:
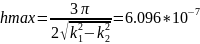
Определить параметры
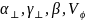 ,
а также используя заданную величину
,
а также используя заданную величину
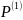 или
или
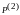 определить
постоянные А и В для низшего типа волны.
определить
постоянные А и В для низшего типа волны.
Параметры и были найдены в пункте 2 в результате графического решения уравнений
Найдем коэффициент фазы:
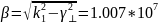
Найдем фазовую скорость:
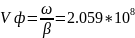 м/с
м/с
Определим постоянные А и В для низшего типа волны:
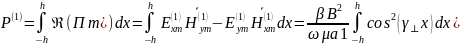
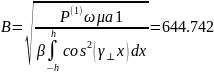
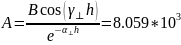
Рассчитать и построить зависимости амплитуд всех составляющих полей от координаты Х для низшего типа волны в средах 1 и 2.
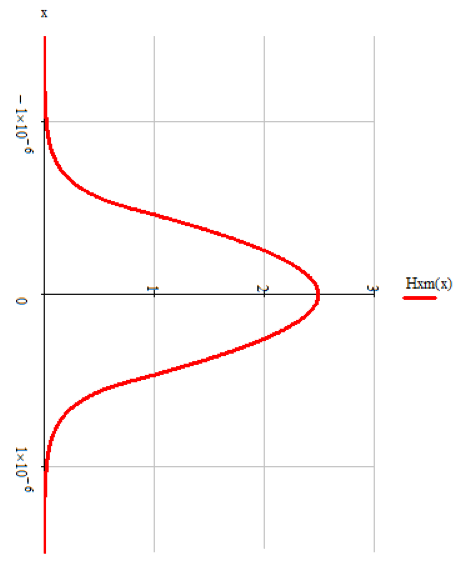
График
зависимости амплитуды
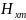 от x
от x
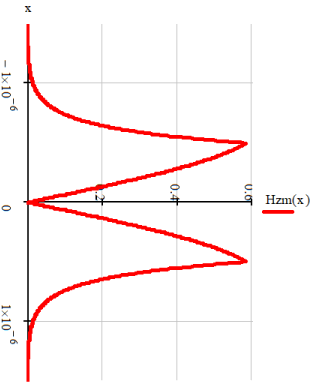
График
зависимости амплитуды
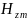 от x
от x
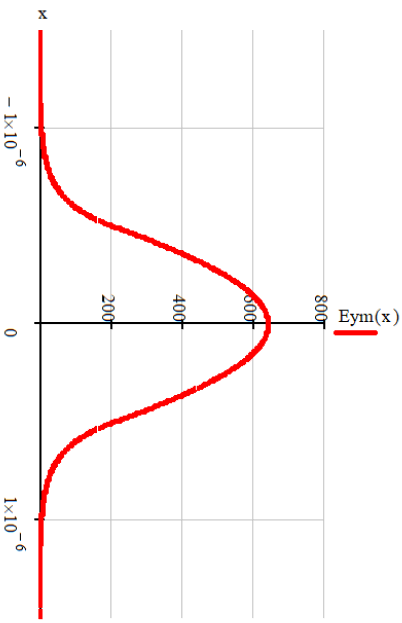
График
зависимости амплитуды
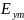 от x
от x
Определить процентное соотношение мощностей и
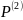 ,
проходящих через поперечное сечение
сред 1 и 2 для низшего типа волны.
,
проходящих через поперечное сечение
сред 1 и 2 для низшего типа волны.
Определим :
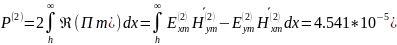 Вт
Вт
Теперь можем определить процентное соотношение мощностей:

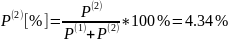
Список литературы:
Конспекты лекций и семинаров
Пименов В.Ю. Вольман В.И. Муравцов А.Д. Техническая электродинамика. 2000г. Издательство “Радио и Связь”, 536с.
Ответы на защиту:
Почему световоды среди всех известных линий передачи имеют минимальное затухание?
Распространение волны в реальной линии передачи сопровождается уменьшением переносимой мощности. Это связано:
1) с рассеянием части мощности в металлических проводниках линии;
2) с затуханием волны в заполняющем диэлектрике;
3) с излучением части мощности в окружающее пространство (в линиях передачи открытого типа).
Многопроводные линии при работе на частотах выше десятка МГц имеют слишком большое затухание, для коаксиальных линий аналогичное явление наступает в диапа-зоне единиц ГГц, металлические волноводы ограничены в работе частотой в 30-40 ГГц, полосковые линии вообще непригодны для передачи на большие расстояния из-за своих конструктивных особенностей. Ограничения по частоте работы вышеуказанных линий во многом вызваны наличием в них проводящих, токоведущих частей. По мере роста частоты у любого проводника, вследствие поверхностного эффекта, возрастает паразитное активное сопротивление, и следовательно, если по этому проводнику течет ток, неизбежно возрастают тепловые потери.
В оптическом диапазоне затухание волны определяется также иными эффектами. На таких частотах величина кванта энергии становится соизмеримой с разностью энергий близко расположенных энергетических уровней атомов диэлектрика. Поэтому под влиянием электромагнитной волны может происходить переход электронов с более низкого энергетического уровня на более высокий, что сопровождается поглощением части энергии волны.
В оптическом диапазоне возникает затухание волн, связанное с так называемым рэлеевским рассеянием
Важнейшей особенностью затухания в оптическом волокне является его независимость от частоты модуляций внутри полосы пропускания. В медных кабелях затухание увеличивается с частотой сигнала: чем больше частота, тем больше затухание. В результате частота сигнала ограничивает расстояние, на которое может быть послан сигнал. Для увеличения этого расстояния требуется повторитель, осуществляющий восстановление сигнала. В оптическом волокне оба эти сигнала будут иметь одинаковое затухание
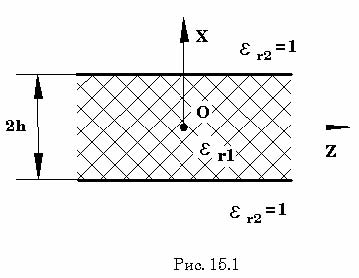
Почему зависимость амплитуды поля от поперечной координаты в первой среде в Вашей пластине может носить только косинусоидальный (синусоидальный) характер для монохроматических полей?
Для монохроматического поля запишем уравнения Максвелла в комплексной форме:

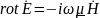
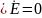
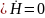
Возьмем ротор от обеих частей второго уравнения Максвелла в комплексной форме и получим:
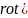
следовательно
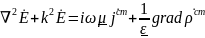
и
аналогично получим для вектора
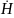
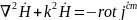
Упростим уравнения для случая отсутствия сторонних источников и окончательно получим волновые уравнения для монохроматического поля:
 (1)
(1)
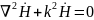
Согласно уравнениям (1), комплексная
амплитуда продольной составляющей
электрического поля в среде 1
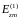 находится из решения уравнения:
находится из решения уравнения:
 ,
(2)
,
(2)
где
 ,
,
 .
(3)
.
(3)
Частными решениями этого уравнения являются выражения:
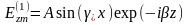 , (4)
, (4)
 .
(5)
.
(5)
Далее, следует определить комплексные
амплитуды поперечных составляющих
полей. Для продольной составляющей
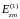 вида (4) выражения для поперечных компонент
поля выражаются через уравнения связи
продольных и поперечных составляющих
векторов поля:
вида (4) выражения для поперечных компонент
поля выражаются через уравнения связи
продольных и поперечных составляющих
векторов поля:
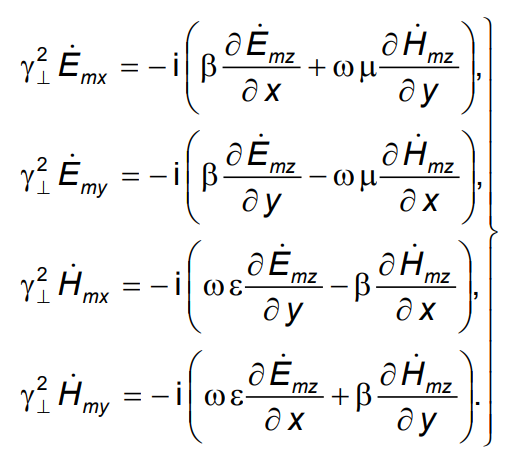 (6)
(6)
И имеют вид:
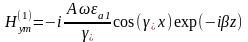 ,
,
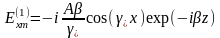 , (7)
, (7)
а для продольной составляющей вида (5) аналогичные выражения записываются как
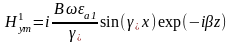
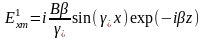 (8)
(8)


