Курсовые / Курсовая работа по ЭМПиВ ч1 8 вариант

Федеральное Агентство Связи Федеральное Государственное Бюджетное Образовательное Учреждение Высшего Образования Ордена Трудового Красного знамени «Московский технический университет связи и информатики»

Кафедра технической электродинамики и антенн

Курсовая работа по дисциплине

«Электромагнитные поля и волны»

«Основные уравнения электродинамики»

Бригада №8

Вариант № 1

Выполнил: ст. гр. БПЗ1802 Аркадьев Илья Дмитриевич Проверил:

Гайнутдинов Тимур Аншарович

Москва 2020

Выполнение

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов и .

Для получения комплексных амплитуд вектора , воспользуемся формулой второго уравнения Максвелла в комплексной форме

Возьмем частные производные:

Получим следующие комплексные амплитуды:

2. Определить диапазон частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси .

Рассматриваемое поле представляет собой волну, бегущую вдоль оси , если

Найдем :

Найдем :

Найдем :

Тогда диапазон частот:

3. Записать выражения для мгновенных значений всех составляющих векторов полей. Рассчитать и построить графики зависимостей мгновенных значений составляющих полей от координаты (при ) в два момента времени и в интервале , где – длина волны в волноводе на частоте .

1) При :

Графики зависимостей мгновенных значений составляющих полей от координаты z

при :

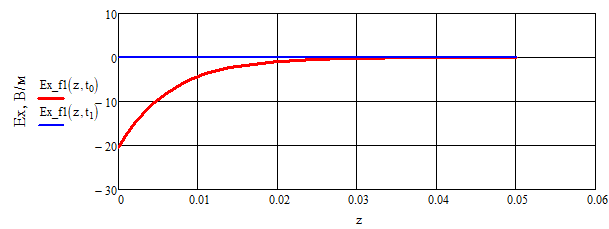
Зависимость Ex от координаты z при и

Зависимость Ey от координаты z при и

Зависимость Ez от координаты z при и

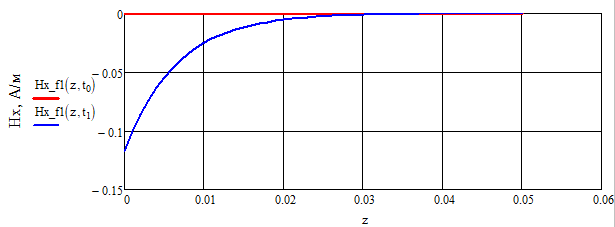
Зависимость Hx от координаты z при и

Зависимость Hy от координаты z при и

2) При :

Графики зависимостей мгновенных значений составляющих полей от координаты z

при :

Зависимость Ex от координаты z при и

Зависимость Ey от координаты z при и

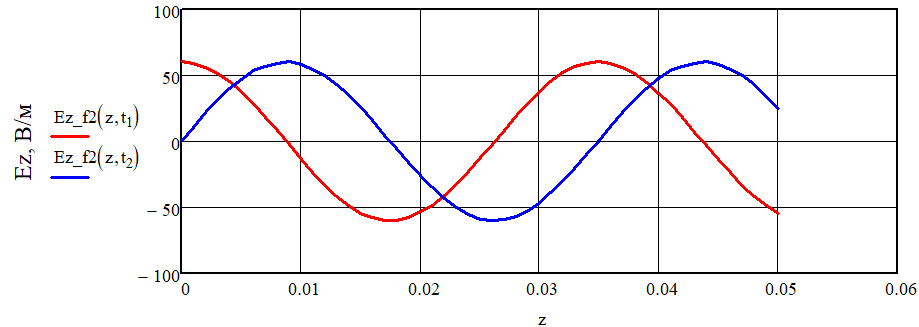
Зависимость Ez от координаты z при и

Зависимость Hx от координаты z при и

Зависимость Hy от координаты z при и

4. Проверить выполнение граничных условий на стенках волновода (при x=0, a и y=0, b)

1 стенка(левая):

2 стенка(правая):

3 стенка(нижняя):

4 стенка(верхняя):

Граничные условия на стенках волновода выполняются

5. Определить максимальные значения плотностей продольного и поперечного поверхностных токов на всех стенках волновода на частоте f₂.

Рассмотрим левую стенку (x=0):

Подставим значения и получим:

Рассмотрим нижнюю стенку (y=0):

Подставим значения и получим:

=

6. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f₂.

7. Определить фазовую скорость V_ф и скорость распространения энергии волны V_э на частоте f₂. Рассчитать и построить графики зависимости этих скоростей от частоты.

График зависимости V_ф и V_э от частоты

8. Нарисовать структуру векторных линий полей и эпюры токов на стенках волновода.

Построим структуру векторных линий полей, выбрав

 

 

 

1. Торец (z = const)

2. Вертикальное продольное сечение ( )

3. Горизонтальное продольное сечение ( )

Запишем выражения для токов на нижней и боковой стенках:

Левая стенка (x=0):

Нижняя стенка (y=0):

Ответы на вопросы: 1) Как связаны между собой 1-е уравнение Максвелла и закон сохранения заряда

Закон сохранения заряда можно сформулировать следующим образом: всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток, втекающий в эту область или вытекающий из нее

Возьмем дивергенцию от обеих частей первого уравнения Максвелла:

Так как дивергенция ротора равна нулю, то

Так как из 3-го ур-ния Максвелла следует, что , то получим:

– ур-ние непрерывности

Проинтегрируем:

2. Возбуждение электромагнитной волны Е11 в прямоугольном волноводе

На практике для ввода или вывода энергии из волновода используют достаточно малые элементы, содержащие электрический или магнитный вибратор, выполняемый в виде малой рамки

При возбуждении волн в линии сле­дует помещать электрический вибратор с током в пучность элек­трического поля параллельно линиям вектора возбуждаемой волны, а рамку с током- в пучность магнитного поля, располагая ее плоскость перпендикулярно вектору .