Добавил:

Adamant Студент, если у тебя есть завалявшиеся работы, то не стесняйся, загрузи их на СтудентФайлс! Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Петербургский государственный университет путей сообщения им. императора Александра I

Предмет:

Теория передачи сигналов

Файл:

Pz_kr_Otsenka_Parametrov_Signala

.pdf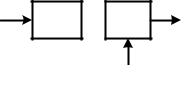

Скачиваний:

Добавлен:

16.07.2022

Размер:

1.53 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Для	максимизации				убывающей			экспоненты	достаточно
минимизировать показатель степени:


		d	1	T
		d	1	0	( y(t) s(t, ))	2		0	(73)
							dt
							dt
		d	N0

Работа приемника аналоговой системы передачи при разных видах модуляции

Амплитудная модуляция

Для случая АМ получаем:

T			T
a y(t) u0 (t)dt (a)2 u02 (t)dt 0 ,
0			0

из уравнения находим оценку
	T
	y(t) u0 (t)dt
	0	,	(74)
	aE	,	(74)
	aE

где E u02 (t)dt - энергия несущего сигнала (на передаче).

0
Приемник,	работающий	по	алгоритму	(73),	может	быть

реализован на одном согласованном фильтре (рис. 2)

y(t)

СФ X

1/(aE)

Рис. 2. Структурная схема приемника.

Частотная модуляция

Для случая ЧМ, аналогично АМ, получаем:

	T	2
d	( y(t) uчм (t, ))	2		0
			dt
			dt
d	0

Рассмотрим	пример, когда		в качестве	несущего сигнала задан сигнал
u0 (t) U 0 sin 0 t . Тогда uчм (t, ) U 0			sin ( 0 a )t ,	а сигнал на входе приемника -
s(t, ) k U 0 sin ( 0	a )t	.
		.
				21

Уравнение правдоподобия примет вид

(t)dt U 2

T sin2

(

a )t dt 2 U 2

y(t) sin

(

a )t

Первый

интеграл

не

зависит от

λ.

Второй

интеграл

представляет

собой энергию посылки, которая также не зависит от λ, так как ЧМ относится к неэнергетическому виду модуляции. Тогда получаем уравнение

y(t) sin

(

a )t dt 0

Непосредственное

решение

этого

уравнения

относительно

оцениваемого параметра затруднительно.

Практически отыскание оценки

сводится

определению

частоты

принимаемого

колеба-

ния, после чего

находится как

Обратимся

снова

уравнению

правдоподобия.

Для

макси-

мизации третьего интеграла

I ( ) y(t) sin( t)dt ,

где

a ,

нужно

построить

функцию I ( ) и

найти её

макси-

мум. Тогда

arg max I ( ) .

Чтобы построить функцию I ( ) ,

можно

взять

дискретный

ряд

значений

аргумента

ω.

Минимальное

число

значений

определяется

теоремой Котельникова в частотной области,

согласно

которой

шаг

по

оси частот

f 1

Tд

Тогда число отсчётов функции I ( )

N F FTд

Вокрестности максимального отсчёта производится интерполяция

полиномом и поиск аргумента точного значения экстремума. При

аппроксимации

полиномом

второй

степени

оценка

частоты

принимаемого колебания получается по следующей формуле:

(75)

Tд

2I m

Здесь ωm -

аргумент максимума,

максимум, I- и

I+ - бли-

жайшие к максимуму значения. Для корректного получения оценок ω по формуле

(75)	на	границах	диапазона	необходимы	два	дополнитель-
ных фильтра.
	Функция	I ( ) представляет собой корреляционный интеграл, дискретные
значения которого			для разных	ω могут	быть	получены на

выходах согласованных фильтров (СФ). Таким образом, приемник должен содержать N+2 согласованных фильтров, решающее устройство для определения максимума ωm, включающее интерполятор (рис. 3). Начальная фаза принимаемого сигнала считается известной.

Фильтры на рис.

3 согласованы

опорными

сигналами sin( l t) ,

l 0 F (2l 1) / Tд ,

l l 0, N 1

СФ0

Решающая

СФ1

схема

max I

СФ

n+1

Рис.3. Схема приемника с использованием согласованных фильтров

Оценка дисперсии погрешности параметра λ

Амплитудная модуляция

Для случая амплитудной модуляции (АМ), относящейся к энергетическим

видам модуляции, дисперсия погрешности оценки D( ) параметра λ находится непосредственно из уравнения (74). Принимаемый сигнал представляет собой смесь сигнала и помехи

y(t) a u0 (t) n(t)

Подставляя это выражение в уравнение (74), получим

(t)dt .

(76)

(a u (t) n(t)) u (t)dt

n(t) u

Из

выражения

(76)

видно,

что

дисперсия

погрешности оценивания

D( )

равна

дисперсии

случайной

величины

обусловленной

аддитивным белым гауссовским шумом.

D( )

n(t) u0 (t)dt

(aE)

После преобразований (проделать самостоятельно) получаем

D( )

(77)

2a2q

2a2 FT

Pс / Pш

где q

Pс

FT - отношение сигнал-шум на входе приемника.

Pш

Расчетные значения D( )= f(Pс/Рш) необходимо свести в таблицу 1.

Таблица 1

(Pс/Рш)

D( )

По

значениям

таблицы

построить

график

зависимости

D( )= f(Pс/Рш)

в логарифмическом масштабе.

Частотная модуляция

Для

частотной

модуляции

(ЧМ)

дисперсия

погрешности

оценки

D( / )

параметра

находится

использованием

неравенства Крамера-Рао:

(78)

D( )

2q / / ( , )

где 2h2 // ( , )

- информация

Фишера,

( , )

T s(t, )s(t, )dt

функция неопределённости сигнала s(t,λ), а Ec - энергия элементарного сигнала на входе приемника:

Ec s 2 (t, )dt .

Рассмотрим пример частотной модуляции, когда в качестве несущего сигнала выбран сигнал u0(t) = U0sinω0t. Тогда

									.
Интеграл							sin 2			a	T
							sin 2			a	T
1		T		0	0				0	0
1									0	0
	T							2 a
		0	cos 2		a	t dt			0	0		0,
		0							0	0
в случае если 0T 1 , или если 0T 2 n								(n 1, 2,...) .

После преобразований

( , 0 ) sin a( 0 )T . a( 0 )T

Вторая производная будет иметь вид:

// ( , 0 )	aT sin a( 0 )T	2	cos a( 0 )T	sin a( 0 )T
	a( 0 )		a( 0 )2	aT ( 0 )3

Значение второй производной при λ - λ0 = 0:

// ( 0 , 0 ) a 2T 2 ,

(вывести самостоятельно).

Подставляя полученное выражение в (78), получаем

							3						3				.
						D( )
						D( )	2		2		2 3		F (P		/ P )
								2qa T			2a T		F (P	c	/ P )
														c		ш
					^
	Расчетные значения D( )= f(Pс/Рш) свести в таблицу 2.
																			Таблица 2

	Pс/Рш	2	4	6		8	10		12			14				16		18	20	25
	^
	D( )

	По	значениям			таблицы		2			построить							график		зависимости
^
D( )= f(Pс/Рш)			в логарифмическом масштабе.

Передача параметра λ в цифровой форме без помехоустойчивого кодирования с использованием двухпозиционной фазовой манипуляции ФМн

Структурная схема системы	передачи	параметра λ в цифровой
форме без помехоустойчивого	кодирования	с использованием двух-
		25

позиционной ФМн содержит источник сообщения (ИС), аналогоцифровой преобразователь (АЦП), модулятор ФМн, канал передачи информации, источник белого гауссовского шума, демодулятор и цифро-аналоговый преобразователь (ЦАП) (рис. 4).

ИС

АЦП

Модуля

Канал (k)

Демодуля

ЦАП

тор

Помеха n(t)

Рис. 4. Структурная схема системы передачи параметра λ в цифровой форме без помехоустойчивого кодирования

Поскольку λ = const на интервале T, то АЦП фактически представляет собой

квантователь			по	уровню	одного	дискретного
отсчёта λk.		Число	разрядов квантователя n выбирается так, чтобы оно
было	максимально		возможным при		заданной полосе	частот	(т. е.
FTд	= 1,	где Тд	- период	следования отсчётов цифрового			сигнала:
	n = Т/Тд = FT.						(18)

Фазовый модулятор модулирует несущее колебание u0(t)= U0cosω0t по фазе. Для двухпозиционного (m=1) сигнала можно записать модулированный сигнал ui(t) в виде:

u0(t)=U0cosω0t при передаче «0», u1(t) = -U0cosω0t при передаче «1».

В качестве демодулятора используется оптимальный когерентный приёмник, работающий по правилу максимума функции правдоподобия (решающее правило по критерию Котельникова при р1 = р0 = 1/2):


	ai arg max f ( y(t) / ai .
	ai
Алгоритм работы приёмника в этом случае имеет вид
	T		T
	( y(t ) s0 (t ))2 dt		( y(t ) s1 (t ))2 dt
	0		0
После преобразований (проделать самостоятельно) можно привести
алгоритм к следующему виду:
		T
		y(t) cos 0tdt 0
		0
Этот	алгоритм можно	реализовать с		использованием	одного
фильтра,	согласованного с	сигналом cosω0t.		Схема такого	демодуля-
тора приведена на рис. 5.
					26

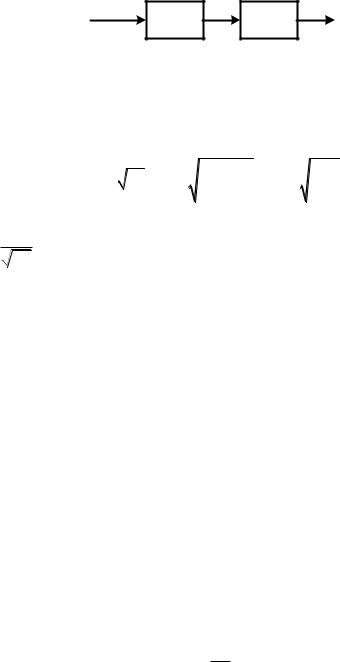
y(t)

СФ РУ

(t=TД)

Рис. 5. Схема демодулятора сигнала ФМ-2 на согласованном фильтре

Вероятность ошибки при когерентном приёме фазоманипулированных сигналов вычисляется по формуле:

Здесь Q(x) 1

e t2 2dt -


	P			P

Q( 2q ) Q 2FTд	c	Q	2	c
				P
	P
	ш			ш

гауссов интеграл ошибок.

Значения функции Q(х) приведены в таблице Приложения. Значения зависимости Pe=f(Pс/Рш) свести в таблицу 3.

Таблица 3

(Pс/Рш)	2	4	6	8	10	12	14	16	18	20	25
pe

Расчётные значения D( )=f (Pс/Рш) занести в таблицу, аналогичную таблице 1, а затем построить график полученной зависимости в логарифмическом масштабе.

Дисперсия погрешности оценки параметра складывается из дисперсии шума квантования и дисперсии шума ошибок:

D( ) Dкв Dош .

Шум квантования представляет собой случайную величину, равномерно распределенную в интервале ( / 2, / 2) , где - шаг квантования:

62n .

Дисперсия шума квантования

Dкв 2 .

Цифро-аналоговый преобразователь (ЦАП) выполняет операцию, обратную АЦП, то есть номер j уровня λ

	n 1
j 2n 1 an 1	2n 2 an 2 ... a0 2i ai .
	i 0
Ошибка в одном из разрядов	ai приводит к тому, что на выходе ЦАП

значение j изменяется на величину 2, в соответствии с номером i ошибочного

разряда. Дисперсию шума, обусловленного такими ошибками, получим складывая дисперсии шума по разрядам:

							n 1							4	n	1
						Dош pe 2 4i					2 pe			4		1		.
						Dош pe 2 4i					2 pe					3		.
							i 0									3
							i 0
Пренебрегая единицей (так как 4n>>1):
							D			2	4n	p .
							D					p .
							ош			3			e
										3
											^
Тогда общая дисперсия погрешности D( ) определяется как:
					2						2
					2						2								Р
			D( )			0, 25 4n		p					0, 25		4n Q 2				с		.
			D( )			0, 25 4n		p					0, 25		4n Q 2						.
					3				e		3								Р
																			ш
					^
Расчетные значения D( )= f(Pс/Рш)										сводятся в таблицу 4.
																							Таблица 4

(Pс/Рш)	2	4		6		8	10			12			14				16			18		20		25
^
D( )

Итак, требуется выполнить четыре задания:

1.Задание – прочитать и разобраться в материале по теме «Оценка параметра сигнала». Вопросы по этой теме будут в итоговом тесте 2 семестра.

2.Задание 1 – стр. 17. Нарисовать структурную схему приемника для оценки

фазы гармонического сигнала. Схему построить по формулам (58 2.3.4) или (59

2.3.5).

3. Задание 2 – стр. 19. Построить зависимости точности (дисперсии) оценок фазы, задержки, частоты, совместной оценки частоты и задержки радиосигнала при значениях q= E/N0 = 1, 5, 10, 30, 50, 100, 1000 и фиксированных значениях:

=1000, 0 =1000000, = 0,01.

Зависимость точности оценки амплитуды радиосигнала построить при длительности радиоимпульса Т= 1,0 мкс; 10,0 мкс; 100,0 мкс; 1,0 мс; 10,0 мс; 20,0 мс и фиксированном значении спектральной плотности мощности помехи 5x10-5 Вт/Гц.

4.Задание 3 – стр. 19. Есть две системы передачи информации:

-аналоговая система передачи информации, осуществляющая передачу информационного параметра λ в аналоговой форме с использованием двух видов модуляции несущего колебания u0 (t): амплитудной АМ, частотной ЧМ;

-цифровая система передачи информации, осуществляющая передачу информационного параметра λ без помехоустойчивого кодирования с использованием двухпозиционной фазовой манипуляции ФМн радиоимпульсами

длительностью Т.

По каналу каждой системы передачи информации, имеющему полосу пропускания F, требуется передать информацию от датчика, измеряющего параметр λ удалённого объекта контроля. Параметр λ имеет нормальное распределение, усечённое границами ± 3а, с M(λ)=0 и с дисперсией σ2 = D (λ). В канале действует помеха, представляющая собой аддитивный белый гауссовский шум с равномерной спектральной плотностью мощности N0.

Приемники систем передачи определяют максимально правдоподобную оценку передаваемого параметра . Критерием сравнения качества приема информационного параметра λ по каналам систем передачи информации является

точность оценки передаваемого параметра D( ), которая зависит от соотношения средней мощности принимаемого сигнала к мощности аддитивного белого

гауссовского шума (Pс/Рш).
Требуется	сравнить	между	собой	зависимости точности оценки
		^
передаваемого	параметра	D( )=	f(Pс/Рш)	для двух	систем передачи при
изменении отношения Рс /Рш в диапазоне 2-25 и сделать					выводы.

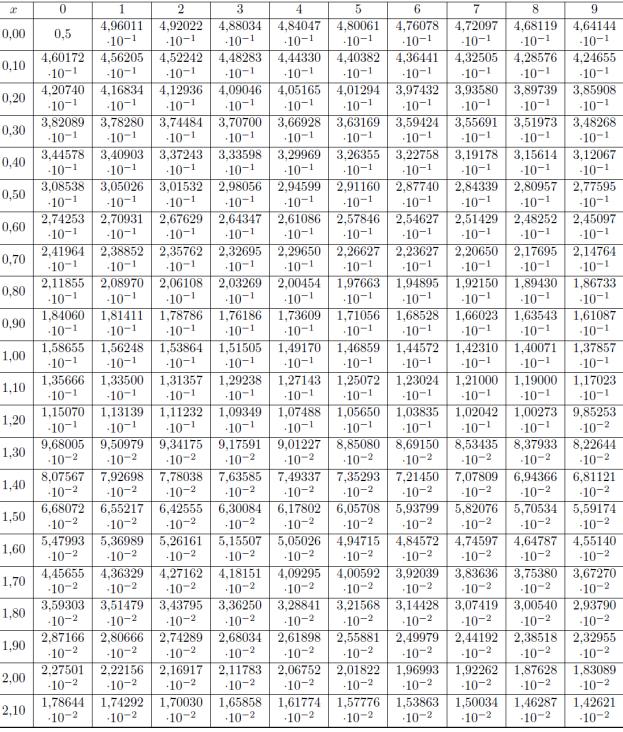
ПРИЛОЖЕНИЕ

Таблица значений функции Q(x)

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете Теория передачи сигналов

#
16.07.20222.5 Mб9MM_dlya_LR.pdf
#
16.07.20221.53 Mб7Pz_kr_Otsenka_Parametrov_Signala.pdf
#
16.07.202287.26 Кб5TPS_12_variant_1.docx
#
03.12.2021271.64 Кб6Амплитудно-импульсная модуляция.ms11
#
17.10.20211.12 Mб11Защита лабы 2 часть 1.jpg
#
17.10.2021864.84 Кб13Защита лабы 2 часть 2.jpg
#
16.07.20225.31 Mб52Лекции по ТПС.pdf