материалы за 2021г / литературные источники / [lect] Рaбинович С.Г. - Погрешности измерений (1987)
.pdf
Чтобы исправить оценку, сделать ее несмещенной, нужно σ~*2
n
поправочный коэффициент n −1 . Тогда получим
~2 |
|
1 |
n |
|
2 |
||
σ |
= |
|
å(xi − x) . |
|
|||
|
|
n −1 i=1 |
|
умножить на
(3-13)
Эта оценка тоже состоятельная, но, как нетрудно проверить, уже несмещенная. Некоторое отклонение от максимума функции правдоподобия для нас менее существенно, чем смещенность оценки.
Среднее квадратическое отклонение случайной величины X — неслучайная величина σ = 
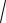D[X ]. Вместо σ 2 приходится взять оценку дисперсии по
формуле (3-13) — случайную величину. Извлечение квадратного корня — процедура нелинейная, она приводит к смещенности получаемой таким
образом оценки σ~ . Чтобы исправить эту оценку, вводят множитель kn , зависящий от п следующим образом:
n……….. |
3 |
4 |
|
|
|
5 |
6 |
7 |
10 |
||
kn……… 1,13 1,08 |
|
1,06 |
1,05 |
1,04 |
1,03 |
||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
1 |
|
n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
σ = kn |
|
|
|
å(xi − x) . |
(3-14) |
|||||
|
n |
|
|
||||||||
|
|
|
|
−1 i=1 |
|
|
|
|
|||
Оценки параметров нормального распределения получены. Но они также являются случайными величинами: повторив измерение, получим другую группу наблюдений, а для нее — другие значения x и σ~ . Рассеивания этих оценок
можно охарактеризовать их средними квадратическими отклонениями σ (x ) и
σ (σ~). Выше мы уже получили, что D(x)= σ 2 . Следовательно, n
σ (x)= |
D[x] |
= |
σ |
(3-15) |
|||
|
|
|
|
||||
|
n . |
||||||
|
|
|
|
|
|||
Поскольку вместо σ возьмем σ~ , то получим оценку значением kn , приходим к известной формуле
|
|
n |
|
σ |
(x )= |
å(xi − x)2 |
|
~ |
|
i=1 |
|
|
|
|
. |
|
|
n(n −1) |
|
Часто σ~(x) обозначают символом Sx .
σ~(x ), Пренебрегая
(3-16)
Аналогично находят оценку среднего квадратического отклонения оценки среднего квадратического отклонения σ~ :
~ ~ |
|
~ |
|
|
|
|
|
||||
|
|
|
σ |
|
|
|
|
||||
|
σ (σ )= |
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|||||
|
|
2(n −1) |
|
||||||||
Отсюда |
|
|
|
|
|
|
|
|
|||
σ~(σ~) |
1 |
|
|
|
|
|
|||||
|
~ |
= |
|
|
|
|
|
. |
|
(3-17) |
|
|
|
|
|
|
|
||||||
|
|
2(n −1) |
|
||||||||
|
σ |
|
|
|
|
|
|||||
Отношение (3.17) характеризует погрешность определения среднего квадратического отклонения. Это отношение зависит только от числа наблюдений в группе и при разных n составляет:
n………..….. |
3 |
5 |
7 |
10 |
15 |
|||
~ ~ |
|
|
|
|
|
|
|
|
100σ (σ ) |
, % |
50 |
35 |
29 |
24 |
15 |
||
|
σ |
|
||||||
|
|
|
|
|
|
|
||
Для надежной оценки погрешности в полученную характеристику нужно ввести еще множитель, примерно равный двум.
Поскольку редко сразу делают очень много наблюдений, то
погрешность в определении среднего квадратического отклонения может быть весьма значительной. Во всяком случае эта погрешность значительно больше погрешности из-за смещенности оценки, обусловленной извлечением квадратного корня и устраняемой поправочным коэффициентом kn . Поэтому
обычно на практике данной смещенностью можно принебречь и вместо формулы (3.14) применять формулу
|
n |
|
|
~ |
å(xi − x)2 |
(3-18) |
|
i=1 |
|||
σ = |
|
. |
|
n −1 |
|||
|
|
3-4 Практические методы проверки
нормальности распределения случайных погрешностей
Обычно задача ставится так: имеется группа результатов наблюдений и высказывается гипотеза о том, что эти наблюдения можно считать
реализациями случайной величины с выбранной формой функции распределения. Затем методами математической статистики эта гипотеза проверяется и либо принимается, либо отвергается.
При большом числе наблюдений (n>50) лучшими критериями проверки данной гипотезы считают критерий согласия К. Пирсона (критерий χ2 ) для группированных наблюдений и критерий Р. Мизеса — Н. В. Смирнова (критерий ω2 ) для негруппированных наблюдений [49.]
Остановимся на критерии χ2 . Идея этого метода состоит в контроле
отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе нормального распределения. Сумма квадратов разностей частот по интервалам не должна
превышать значений χ2 , для которых составлены таблицы в зависимости от
уровня значимости критерия q и числа степеней свободы k = L − 3, где L — число интервалов.
Вычисления ведутся по следующей схеме [31].
1. Вычисляют среднее арифметическое наблюдений и оценку среднего квадратического отклонений по формулам (3.11) и (3.18):
|
|
|
|
n |
|
|
|
|
|
x = |
åxi |
|
|
|
|
|
|
i=1 |
, |
|
|
||
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
σ = |
|
å(xi − x)2 |
. |
|||
|
~ |
|
i=1 |
|
|
|
|
|
|
|
|
n −1 |
|
|
|
2. |
Группируют наблюдения по интервалам. При числе наблюдений |
||||||
40–100 обычно принимают 5–9 интервалов. Для каждого интервала вычисляют середину xi0 и подсчитывают число наблюдений, попавшее в каждый интервал, ϕ~i .
3. Вычисляют число наблюдений для каждого из интервалов, теоретически соответствующее нормальному распределению. Для этого
сначала от реальных середин интервалов xi0 переходят к нормированным zi :
= x − x
zi i0 ~
σ
Затем для каждого значения zi находят значение функции плотности
вероятностей
f (zi )= |
|
1 |
|
e− |
zi2 |
||
|
|
2 |
|
||||
|
|
|
|||||
2π |
|||||||
|
|
. |
|||||
Вычисление f (zi ) ведется с помощью табл. П-1 приложения. |
|||||||
Теперь можно вычислить ту часть |
|
ϕi общего числа имеющихся |
|||||
наблюдений, которая теоретически должна была быть в каждом из интервалов:
ϕi = n h~ f (zi )
σ,
где n — общее число наблюдений, h = xi0+1 − xi0 — длина интервала, принятая при построении гистограммы.
4. Если в какой-либо интервал теоретически попадает меньше 5 наблюдений, то его в обеих гистограммах
соединяют с соседним
интервалом. Затем определяют число степеней свободы k = L − 3, где L — общее число интервалов (если произведено укрупнение интервалов, то L — число интервалов после укрупнения).
5. Вычисляют показатель разности частот χ 2 :
L |
, где χi2 |
|
~ |
2 |
χ2 = åχi2 |
= |
(ϕi −ϕi |
) . |
|
i=1 |
|
|
ϕi |
|
6. Выбирают уровень значимости критерия q. Уровень значимости должен быть достаточно малым, чтобы была мала вероятность отклонить правильную гипотезу (совершить ошибку, первого рода). С другой стороны, слишком малое значение q увеличивает вероятность принять ложную гипотезу, т. е. совершить ошибку второго рода [49, стр. 250].
По уровню значимости q и числу степеней свободы k в табл. П-3 находим границу критической области χq2 , так что
P{χ2 > χq2}= q .
Вероятность того, что получаемое значение χ 2 превышает χq2 равна q и мала. Поэтому, если оказывается, что χ2 > χq2 , то гипотеза о нормальности отвергается. Если χ2 < χq2 , то гипотеза о нормальности принимается.
Чем меньше q, тем при том же k больше значение χ 2 , тем легче выполняется условие χ2 < χq2 и принимается проверяемая гипотеза. Но при
этом увеличивается вероятность ошибки второго рода. Поэтому нецелесообразно брать q<0,01. При слишком большом q, как указывалось выше возрастает вероятность ошибки первого рода и, кроме того, снижается чувствительность критерия. Например, при q — 0,5 с равной вероятностью χ 2 может быть и больше и меньше χq2 и, следовательно,
теряется возможность сделать выбор в пользу проверяемой гипотезы или против нее.
Для единообразия решения рассматриваемой задачи желательно унифицировать применяемые уровни значимости. С этой целью можно
предложить попытаться ограничить выбор уровня значимости интервалом
0,02 ≤ q ≤ 0,1.
Наряду с рассмотренной проверкой, при которой была принята односторонняя критическая область, применяют и двусторонние критические области, т.е. оценивается P{χн2 < χ2 < χв2}= q . В этом есть
определенный смысл, так как у реальной группы данных очень малое значение χ 2 маловероятно. Уровень значимости критерия q делится на две
части: q = q1 + q2 . |
Для простоты часто считают q1 = q2 . По табл. П-3 для |
||
P{χ2 |
> χ2} находят χ 2 |
для уровня значимости q и числа степеней свободы k |
|
|
q |
1 |
1 |
и χ22 |
для уровня значимости 1—q2 и того же k.. Гипотеза о нормальности |
||
проверяемой группы данных принимается, если χ22 ≤ χ2 ≤ χ12 .
Следует еще раз отметить, что данный критерий позволяет проверять
соответствие эмпирических данных любому теоретическому распределению, а не только нормальному. Однако этот критерий, как, впрочем, и другие критерии согласия, не позволяет установить вид распределения наблюдений, а лишь дает возможность проверить, допустимо ли отнести их к нормальному или иному, выбранному заранее распределению.
В практике измерений часто возникает необходимость проверить гипотезу о нормальности небольшой группы наблюдений. Гипотеза согласно рекомендации [31] проверяется с помощью двух критериев.
|
|
Критерий 1. |
По данным наблюдений x1,..., xn |
вычисляем значение |
||||||||||||||||||||
параметра d по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
å |
|
xi − x |
|
|
|
|
|
|
|
(3-19) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
d = |
i=1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
nS* |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= |
|
|
|
å(xi − x)2 |
|
(3-20) |
||||||||||||
|
|
|
|
|
S* |
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
dq1 |
Выбираем затем уровень значимости критерия q1 |
и по табл. П-4 находим |
||||||||||||||||||||||
и d |
q1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Принимаем, что гипотеза о нормальности по критерию 1 не |
||||||||||||||||||||||
отвергается, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
d1− |
q1 |
≤ d ≤ d |
q1 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
В противном случае гипотеза отвергается. |
|
|
|
|||||||||||||||||||
|
|
Критерий 2. |
Этот критерий |
|
|
введен |
|
|
|
дополнительно для проверки |
||||||||||||||
«концов» распределений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Принимаем, |
что гипотеза |
о |
нормальности |
по критерию |
2 |
не |
||||||||||||||||
отвергается, если не более m разностей |
|
xi − x |
|
~ |
где |
σ~ |
||||||||||||||||||
|
|
|||||||||||||||||||||||
|
превзошли zασ , |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
-верхняя 100 α |
2 |
|
|
||||||||||
вычисляется по формуле (3-18), а |
|
zα |
-процентная квантиль |
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||
нормированной функции Лапласа (табл. П-2); α определяем по п и уровню значимости q как корень уравнения
n |
|
1− åCnk (1−α )k α n−k = q |
. |
i=1 |
Для нахождения α по заданным п, q и m=1 или 2 составлена табл. П-5.
При 10 < n < 20 следует принимать m = 1. Если 50 > n ³ 20 , то т=2.
Если число разностей xi − x , больших zα σ 2 , превышает т, то
2
гипотеза о нормальности отвергается.
Гипотеза о нормальности принимается, если для проверяемой группы данных выполняются оба критерия.
Уровень значимости составного критерия
q ≤ q1 + q2 ,
где q1 — уровень значимости для критерия 1, q2 — уровень значимости для критерия 2.
3-5. Примеры проверки нормальности распределения результатов наблюдений
П р и м е р 1 . В результате измерений получено 200 отклонений размера некоторой детали от номинального значения. Эти данные сгруппированы в 14 интервалов, середины которых, число отклонений, попавших в каждый интервал, и вспомогательные данные для расчетов по рассмотренной в § 3-4 схеме приведены в табл. 3-1 [31].
Кроме того, по формулам (3-11) и (3-18) вычислены среднее отклонение от номинального размера и оценка среднего квадратического отклонения x = −0,0284 и σ~ = 0,0515 . Как показано в таблице, в итоге
получено χ 2 = 7,03 .
Так как после укрупнения интервалов L = 11, то k=L—3=8.
Возьмем двустороннюю критическую область, и q1 = q2 = 0,02 . По табл. П-3 из условия
P{χ 2 > χq2}находим χ12 = 18,2 , а из условия P{χ 2 > χq2}= 1 - q2 находим χ22 = 2,03 .
Так как 2,03<7,03<18,2, то гипотеза о нормальности полученных отклонений принимается.
П р и м е р 2. В табл. 3-2 приведены результаты наблюдений, полученные при измерении напряжения исследуемого источника с помощью потенциометра. Проверим, можно ли считать полученные данные реализациями случайной величины, имеющей нормальное распределение.
Сначала найдем оценки параметров распределения
136
x= å x1 = 2,7994 В 36 i=1
~ |
1 |
36 |
2 |
1478×10−8 |
|
|
−4 |
|
σ = |
|
å(xi |
- x) = |
|
= 6,52 ×10 |
|
В. |
|
|
35 |
|
||||||
|
35 i=1 |
|
|
|
|
|
||
и по формуле (3-20) найдем S* :
S* = 6,52 ×10−4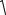 
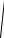3536 = 6,41×10−4 В.
Затем проверим выполнение критериев 1 и 2.
Таблица 3-1
Исходные данные и промежуточные выкладки для вычисления χ 2
|
Середина |
Эмпирическое |
|
|
|
|
xi0 − x |
|
|
|
|
|
Теоретическое |
|
Номер |
интервала |
число |
|
|
|
|
|
|
|
h |
число |
2 |
||
|
|
|
|
|
|
|
|
|
||||||
интервала i |
x |
наблюдений в |
xi0 − x |
zi |
= |
|
~ |
|
f (zi ) |
|
~ |
f (zi ) |
наблюдений в |
χi |
|
~ |
|
|
|
|
σ |
|
|
|
σ |
интервале ϕi |
|
||
|
i0 |
интервале ϕi |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-0,14 |
3 |
-0,1116 |
|
-2,17 |
|
0,038 |
|
0,015 |
3,0 |
0,27 |
|||
2 |
-0,12 |
8 |
-0,0916 |
|
-1,78 |
|
0,082 |
|
0,032 |
6,4 |
0,27 |
|||
3 |
-0,10 |
11 |
-0,0716 |
|
-1,39 |
|
0,174 |
|
0,068 |
13,6 |
0,50 |
|||
4 |
-0,08 |
20 |
-0,0516 |
|
-1,00 |
|
0,242 |
|
0,094 |
18,8 |
0,08 |
|||
5 |
-0,06 |
27 |
-0,0316 |
|
-0,61 |
|
0,333 |
|
0,130 |
26,0 |
0,04 |
|||
6 |
-0,04 |
36 |
-0,0116 |
|
-0,23 |
|
0,388 |
|
0,151 |
30,2 |
1,11 |
|||
7 |
-0,02 |
29 |
+0,0084 |
|
+0,16 |
|
0,394 |
|
0,154 |
30,8 |
0,10 |
|||
8 |
0,00 |
18 |
+0,0284 |
|
+0,55 |
|
0,343 |
|
0,134 |
26,8 |
2,89 |
|||
9 |
0,02 |
17 |
+0,0484 |
|
+0,94 |
|
0,256 |
|
0,099 |
19,8 |
0,40 |
|||
10 |
0,04 |
17 |
+0,0684 |
|
+1,33 |
|
0,165 |
|
0,064 |
12,8 |
1,38 |
|||
11 |
0,06 |
8 |
+0,0884 |
|
+1,72 |
|
0,091 |
|
0,035 |
7,0 |
0,14 |
|||
12 |
0,08 |
4 |
+0,1084 |
|
|
+2,1 |
|
0,044 |
|
0,017 |
3,4 |
0,12 |
||
13 |
0,10 |
1 |
+0,1284 |
|
+2,49 |
|
0,018 |
|
0,007 |
1,4 |
0,12 |
|||
14 |
0,12 |
1 |
+0,1484 |
|
+2,88 |
|
0,006 |
|
0,002 |
0,4 |
0,12 |
|||
Сумма |
— |
200 |
Примерно 0 |
|
|
|
— |
|
— |
|
|
— |
200,4 |
7,03 |
Таблица 3-2
Результаты наблюдений, полученные при измерении напряжения источника, и
предварительные вычисления
Номер |
Показания |
|
|
|
|
|
|
|
|
|
|
Номер |
|
|
|
Показания |
|
|
|
||||||
наблюдения |
|
(xi - x )×104 |
(xi - x)2 ×108 |
|
|
|
|
|
|
(xi - x)2 ×108 |
|||||||||||||||
i |
потенциометра |
|
наблюдения |
|
|
|
потенциометра |
(xi - x )×104 |
|||||||||||||||||
|
xi, В |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
xi, В |
|
|
|
|||
1 |
2.7997 |
|
+3 |
|
|
9 |
|
|
|
|
19 |
|
|
|
|
|
2.7988 |
-6 |
|
36 |
|||||
2 |
2.7991 |
|
-3 |
|
|
9 |
|
|
|
|
20 |
|
|
|
|
|
2.7999 |
+5 |
|
25 |
|||||
3 |
2.7990 |
|
-4 |
|
|
16 |
|
|
|
|
21 |
|
|
|
|
|
2.7998 |
+4 |
|
16 |
|||||
4 |
2.7997 |
|
+3 |
|
|
9 |
|
|
|
|
22 |
|
|
|
|
|
2.7996 |
+2 |
|
4 |
|||||
5 |
2.7992 |
|
-2 |
|
|
4 |
|
|
|
|
23 |
|
|
|
|
|
2.7992 |
-2 |
|
4 |
|||||
6 |
2.7976 |
|
-18 |
|
|
324 |
|
|
|
|
24 |
|
|
|
|
|
2.8000 |
+6 |
|
36 |
|||||
7 |
2.7984 |
|
-10 |
|
|
100 |
|
|
|
|
25 |
|
|
|
|
|
2.7993 |
-1 |
|
1 |
|||||
8 |
2.7999 |
|
+5 |
|
|
25 |
|
|
|
|
26 |
|
|
|
|
|
2.7988 |
-6 |
|
36 |
|||||
9 |
2.7990 |
|
-4 |
|
|
16 |
|
|
|
|
27 |
|
|
|
|
|
2.7993 |
-1 |
|
1 |
|||||
10 |
2.7989 |
|
-5 |
|
|
25 |
|
|
|
|
28 |
|
|
|
|
|
2.7982 |
-12 |
|
144 |
|||||
11 |
2.7997 |
|
+3 |
|
|
9 |
|
|
|
|
29 |
|
|
|
|
|
2.7999 |
+5 |
|
25 |
|||||
12 |
2.7993 |
|
-1 |
|
|
1 |
|
|
|
|
30 |
|
|
|
|
|
2.7997 |
+3 |
|
9 |
|||||
13 |
2.8000 |
|
+6 |
|
|
36 |
|
|
|
|
31 |
|
|
|
|
|
2.7999 |
+5 |
|
25 |
|||||
14 |
2.8006 |
|
+12 |
|
|
144 |
|
|
|
|
32 |
|
|
|
|
|
2.7992 |
-2 |
|
4 |
|||||
15 |
2.7998 |
|
+4 |
|
|
16 |
|
|
|
|
33 |
|
|
|
|
|
2.7999 |
+5 |
|
25 |
|||||
16 |
2.7995 |
|
+1 |
|
|
1 |
|
|
|
|
34 |
|
|
|
|
|
2.7989 |
-5 |
|
25 |
|||||
17 |
2.7992 |
|
-2 |
|
|
4 |
|
|
|
|
35 |
|
|
|
|
|
2.7994 |
0 |
|
0 |
|||||
18 |
2.8011 |
|
+17 |
|
|
289 |
|
|
|
|
36 |
|
|
|
|
|
2.7999 |
+5 |
|
25 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Критерий 1. Для того чтобы согласно (3-19) вычислить значение d, сначала подсчитаем |
|
|||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
å |
|
xi - x |
|
= 174 ×10-4 . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Затем находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d = |
|
174 ×10-4 |
|
|
= 0,754 |
|
|
|
|
||||||||||||
|
|
|
|
36 ×6,41×10-4 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выбрав уровень |
значимости |
q1 = 0,02 , из |
|
|
табл. П-4 находим |
d0,01 = 0,877 |
и |
|||||||||||||||||
d0,99 = 0,717 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Так как 0,717<0,754<0,877, то критерий 1 выполняется. |
|
|
|
|
|
|||||||||||||||||||
|
Критерий 2. Примем уровень значимости q2 = 0,02. По табл. П-5 для n = 36 и q = 0,02 |
||||||||||||||||||||||||
находим α = 0,99. Тогда, обращаясь, к табл. П-2, находим zα |
= 2,58 . Отсюда |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
~ |
|
|
|
|
|
|
|
|
-4 |
=16,8 |
×10 |
-4 |
|
|
|
|||||||
|
|
|
zασ = 2,58× 6,52 ×10 |
|
|
. |
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Согласно критерию 2, не более двух разностей |
|
|
|
x - x |
|
|
могут превзойти 16,8 ×10-4 . По |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
данным, приведенным в табл. 3-2, видим, что разности |
|
x1 - x |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
только при i = 6 и i = 18 превышают критическое значение. Следовательно, критерий 2 выполняется.
Таким образом, с уровнем значимости q ≤ q1 + q2 = 0,04 гипотеза о нормальности полученных данных согласуется с данными наблюдений,
3-6. Обнаружение грубых погрешностей
Если в полученной группе результатов наблюдений одно-два резко отличаются от остальных, а наличие описки, ошибки в снятии показаний и тому подобных промахов не установлено, следует проверить, не являются ли они грубыми погрешностями, подлежащими исключению. Задача решается статистическими методами, основанными на том, что распределение, к которому относится рассматриваемая группа наблюдений, можно считать нормальным.
Для этого случая Ф. Е. Граббс рассчитал границы допустимых максимальных и минимальных значений при п наблюдений.
В дальнейшем были табулированы q-процёнтные точки
распределения максимальных по модулю отклонений результатов наблюдений от их среднего значения
tГ = |
max |
|
x − x |
|
|
|
|
|
|
|
|||||
|
|
|
i |
|
|
(3-21) |
|
|
|
|
~ |
|
|
||
|
|
σ |
|
||||
здесь σ 2 — оценка среднего |
|
|
квадратического |
отклонения, |
|||
вычисляемая по формуле (3-18). Это распределение удобнее для расчетов и приведено в табл. П-6 [6].
Чтобы проверить возможность отбросить наблюдение хв, нужно
сначала вычислить
|
t = |
|
|
x |
− x |
|
|
|
|
|
|
|
|
||||
|
|
|
в |
~ |
|
|
(3-22) |
|
|
|
|
||||||
|
|
|
|
|
|
|||
|
~ |
|
|
|
σ |
|
||
где x |
|
|
|
|
|
|
|
|
и σ вычисляют с учетом всех п результатов наблюдений. |
|
|||||||
Затем, выбрав уровень значимости q, нужно найти в |
табл. П-6 |
|||||||
значение tГ , отвечающее этому уровню и числу наблюдений.
Если t > tГ , то хв можно отбросить: вероятность появления наблюдения, дающего t > tГ , мала и равна принятому уровню значимости.
Суменьшением q растет tГ и условие t > tГ выполняется труднее.
Пр и м е р 1 . Измерение силы тока дало следующую группу данных (сила тока в миллиамперах): 10,07; 10,08; 10,10; 10,12; 10,13; 10,15; 10,16; 10,17; 10,20; 10,40. Наблюдение с результатом 10,40 резко отличается от остальных. Проверим, нельзя ли его отбросить. Воспользуемся приведенным критерием, хотя у нас и нет данных для того, чтобы считать эти наблюдения удовлетворяющими нормальному распределению:
x=10,16 мА,
σ~ = 0,094 мА,
t = 10,40 −10,16 = 2,55 0,094
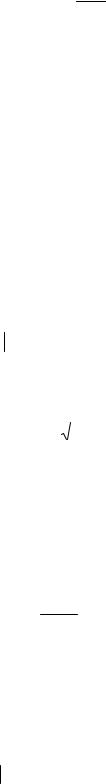
Примем q=1%. По табл. П-6 находим tГ = 2,62. Так как t < tГ , то наблюдение 10,40 нельзя
отбросить.
П р и м ер 2. Рассмотренный критерий основан на предположении о нормальном распределении наблюдений. Интересно посмотреть, что он даст в случае, когда о распределении ничего нельзя
сказать. Допустим, что x1 = 0 , x2 = 0, x3 = 0 , x4 = 4 . Может быть, x4 можно отбросить? Приведем вычисления:
~x = 1, σ~ = 2, t = 4 2-1 = 1,5.
Как видно из табл. П-6, при n=4 и любом q всегда tГ >1,6 . Поскольку t < tГ , то отбросить x4 нельзя. По-видимому, целесообразно продолжить измерение и увеличить число наблюдений.
3-7. Доверительные интервалы
~
Получив оценку A , представляет интерес выяснить, насколько она может изменяться при повторных измерениях, выполняемых в тех же условиях. Этот
вопрос выясняется с помощью построения доверительного интервала для истинного значения измеряемой величины.
Доверительным интервалом называется интервал, который с заданной вероятностью, называемой доверительной, накрывает истинное значение измеряемой величины,
В общем случае доверительные интервалы можно строить на основе неравенства Чебышева [49, стр. 183]
P{ |
X - A |
|
³ tσ}£ |
1 |
, |
|||||||
|
||||||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
t2 |
|||
Для случайной величины x имеем |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
ì |
|
|
|
|
tσ ü |
|
1 |
|
||||
|
|
|
|
|
||||||||
Pí |
x - A |
|
³ |
|
|
|
ý £ |
|
|
|
||
|
|
|
|
|
t2 |
|||||||
|
|
|
|
|||||||||
î |
|
|
|
|
|
n þ |
|
|||||
При этом не требуется знать вида распределения наблюдений, но нужно |
||||||||||||
знать σ [X ]. Однако получаемые с |
|
помощью неравенства Чебышева |
||||||||||
интервалы оказываются слишком широкими для практики, и они не получили применения.
Обычно доверительные интервалы строят, основываясь на распределении Стьюдента, которым называют распределение случайной величины
= x - A
t (3-23)
Sx
вычисленное для X с нормальным распределением, Sx — оценка среднего
квадратического отклонения, среднего арифметического, вычисляемая по формуле (3-16).
Доверительный интервал [x − tqSx , x + tqSx ] отвечает вероятности
P{ |
x - A |
|
£ tqSx }= α |
(3-24) |
|