6 семестр / Физическая химия 2-ая аттестация 6 семестр

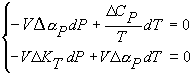 (3.25)

Однородная система линейных уравнений (3.25) имеет ненулевое решение при условии равенства нулю определителя системы:

 (3.26)

Таким образом, скачки вторых производных не являются независимыми, а связаны между собой соотношением (3.26). Решение системы уравнений (3.25) при условии (3.26) имеет вид: (3.27)

Формулы (3.26) и (3.27) называются уравнениями Эренфеста.

В отличие от кривой фаз равновесия Клайперона-Клаудиуса, это ур-ие определяет линию фазового перехода, т.к. при фазовых переходах 2-го рода не существует метастабильных состояний. Новая фаза появляется сразу во всем объеме вещества и, соответственно, не существует межфазной поверхности раздела и поверхностной энергии.

Интересно, что предположения о возможности метастабильных фазовых состояний при фазовых переходах 2-го рода приводит к выводу о том, что фазовые переходы 2-го рода вообще не возможны. Действительно, в точке непрерывного фазового перехода точка пересечения m ₁ и m ₂ должна быть и точкой касания (общая касательная), но в случае простого касания m _2 < m ₁, как при T > T₀, так и при T < T₀, т.е. перехода быть не может. Следовательно нужно, чтобы точка T₀ была точкой перегиба кривых m ₁(T) и m ₂(T), что означает в этом случае разрывной функцией может быть только третья производная, что соответствует фазовому переходу 3-го рода.

Таким образом, теория Эренфеста дает связь между скачками соответствующих термодинамических коэффициентов (3.26) и определяет производную линию фазового превращения (3.27).

Взаимосвязь составов пара и ж для идеальных и неидеальных ра-ров Если компоненты А и В смеси обладают близкими свойствами (сходное строение молекул и близкие молекулярные массы, одинаковая полярность и т.д.), то можно считать одинаковыми и силы взаимодействия F между однородными и разнородными молекулами, т.е. FA-A = FB-B = FА-В

Образование ра-ра из этих компонентов не сопровождается изменением суммарного объема и теплового эффекта. При этом изменение состава ра-ра не приводит к образованию новой фазы (например, к кристаллизации одного из компонентов). Такие ра-ры называются идеальными. В качестве примеров ра-ров, близких к идеальным, можно привести смеси оптических изомеров амилового спирта; смеси, компоненты которых отличаются по изотопному составу: Н2О – Д2О. К ним близки по свойствам смеси изомеров н-С5Н12- изо-С5Н12и гомологов С6Н12-С7Н16.

Давление пара над ра-ром зависит от температуры и состава ра-ра, а при постоянной температуре – только от состава.

Идеальные ра-ры подчиняются закону Рауля, согласно которому парциальное давление пара компонента над ра-ром равно произведению давления пара чистого компонента на его мольную долю в ра-ре: отвечающее уравнению прямой (рисунок 2.1).В этой формулировке з-н Рауля справедлив для низких давлений. Р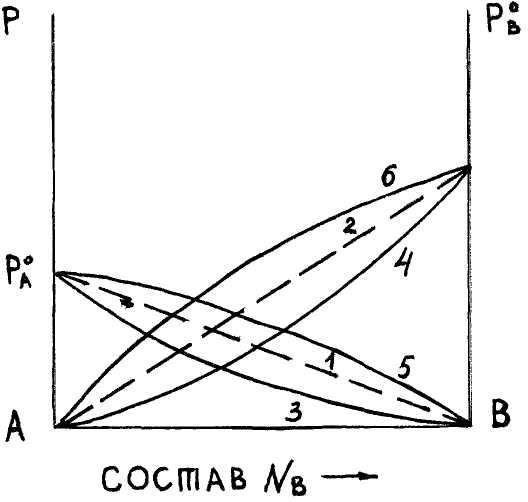 исунок 2.1. Давление пара системы А-В.1-2 – изменение парциальных давлений компонентов А и В для случая образования идеальных ра-ров.3-4 – изменение парциальных давлений компонентов А и В для случая отрицательных отклонений их от закона Рауля.5-6 – изменение парциальных давлений компонентов А и В для случаев положительных отклонений их от закона Рауля. Неидеальные ра-ры. Отклонения от идеальности обусловлены как физическими, так и химическими причинами (дипольные взаимодействия, поляризация, различная интенсивность Ван-дер-Вальсовых сил, ассоциация, диссоциация, сольватация и др.). Все эти взаимодействия настолько переплетаются, что трудно предугадать суммарный результат. Однако благодаря преобладанию одной из форм взаимодействия, можно произвести классификацию ра-ров по признаку отрицательного или положительного отклонения от закона Рауля.

Если силы взаимодействия между однородными частичками А-А и В-В меньше, чем разнородными А-В, то есть если FА-А<FА-В>FВ-В, то имеет место стремление к взаимодействию компонентов, которые вызывают повышение ра-римости. Образование ра-ра сопровождается выделением тепла. Поэтому теплота парообразования компонентов из ра-ра оказывается большей, чем чистого компонента. Затруднение парообразования означает понижение давления пара. В этом случае говорят об отрицательном отклонении от закона Рауля (рисунок 2.1, кривые 3-4). Образование ра-ра как правило сопровождается уменьшением объема.

Если силы взаимодействия между однородными молекулами А-А и В-В больше, чем между разнородными А-В, т.е. если FА-А>FА-В<FВ-В, то процесс ра-рения сопровождается поглощением тепла. Это приводит к уменьшению теплоты парообразования, т.е. облегчает испарение. Если одинаковые молекулы стремятся к ассоциации, то ра-римость по сравнению с идеальной (рассчитанной по закону Рауля) понижается. Образование ра-ра, как правило, сопровождается увеличением объема. В этом случае говорят о положительном отклонении от закона Рауля (рисунок 2.1, кривые 5-6).

Весьма значительные положительные отклонения от закона Рауля приводят к нарушению гомогенности – обе жидкости оказываются ра-римыми до определенного предела.

Влияние температуры не одинаково сказывается на ограниченной ра-римости жидкостей, это зависит от того, вступает ли они друг с другом в химические взаимодействие или нет. В случае, когда жидкости химически не взаимодействуют, изменение температуры влияет на ра-римость лишь постольку, поскольку оно вызывает перераспределение энергии движения между молекулами. С ростом температуры увеличивается доля молекул с повышенным запасом энергии, способных, благодаря этому осуществить работу перехода из одной жидкости в другую. С ростом температуры взаимная ра-римость таких жидкостей будет увеличиваться. Составы сопряженных ра-ров будут все более и более сближаться и при некоторой температуре станут тождественными. Начиная с этой температуры и выше, будет наблюдаться неорганичная ра-римость жидкостей друг в друге. Температура, начиная с которой жидкости неограниченно смешиваются друг с другом, получила название верхней критич. температуры ра-рения.

В тех случаях, когда ограниченно ра-римые жидкости образуют молекулярные соединения, повышение температуры уменьшают их взаимную ра-римость. Повышение температуры способствует диссоциации сложных молекул в более простые, плохо ра-римые компоненты, что и ведет к уменьшению взаимной ра-римости. Наоборот, при понижении температуры взаимная ра-римость увеличивается. Может случиться, что прежде чем сопряженные ра-ры начнут затвердевать, состав их станет одинаковым. Температура, при которой это происходит, получила название нижней критической температурой ра-рения. Бывают такие смеси, которые обладают двумя критическими температурами ра-рения: верхней и нижней.

В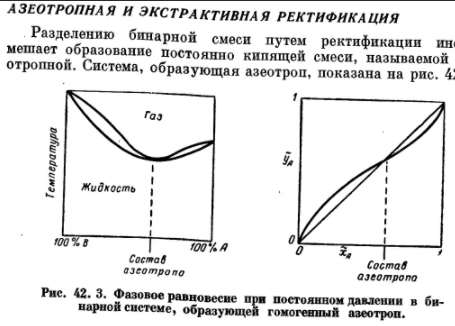 ода–фенол в жидком состоянии проявляют ограниченную ра-римость, а в твердом – полностью нера-римые друг в друге. Ограниченную ра-римость ж можно наблюдать на примере системы анилин-вода Азеотропные смеси и их св-ва. Азеотро́пная смесь — смесь двух или более жидкостей с таким составом, который (при данном конкретном давлении) не меняется при кипении, то есть составы равновесных жидкой и паровой фаз совпадают.

Точка на фазовой диаграмме, которая соответствует равенству составов жидкости и пара, называется азеотропной точкой. Температура кипения для азеотропной смеси может быть как меньше (положительные азеотропы), так и больше (отрицательные азеотропы) температуры кипения низкокипящего компонента. Термодинамика не накладывает ограничений на число азеотропных точек в системе[1]. В основном известны бинарные ра-ры с одной азеотропной точкой. При изменении давления изменяется не только температура кипения, но и состав азеотропной смеси, этим они отличаются от чистых жидкостей. Законы Гиббса-Коновалова. Установливают соотношения между составами равновесных жидких ра-ров и составами их паров, а также общим давлением насыщенного пара над ними. Первый закон Гиббса-Коновалова гласит: в насыщенном паре над ра-ром преобладает по сравнению с ра-ром тот компонент, добавление которого к ра-ру приводит к возрастанию общего давления насыщенного пара (пар обогащен легколетучим компонентом). Данный закон выполняется для любых ра-ров, а на рассматриваемом явлении основана фракционная перегонка (ректификация), позволяющая разделить смесь взаимно-ра-римых жидкостей. Докажем первый закон Гиббса-Коновалова, для чего воспользуемся уравнением Дюгема-Маргулеса (8.10), устанавливающим связь между изменениями парциальных давлений пара компонентов и составом ра-ра при постоянных температуре и давлении. В расчете на 1 моль жидкого бинарного ра-ра указанное уравнение принимает вид х1dlnP1+x2dlnP2=0 . (8.35)

Преобразуем уравнение (8.35): . (8.36) Учтем, что ,  , тогда . (8.37)

Поскольку P=P1+P2,dP=dP1+dP2 ,то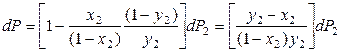 . (8.38)

Разделим правую и левую части уравнения (8.38) на dx₂, получим: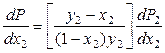 . (8.39)

Поскольку производная (dP₂/dx₂) > 0 (парциальное p второго компонента в паре увеличивается с ростом его мольной доли в ра-ре), то знак производной (dP/dx₂) определяется знаком разности (y₂ – x₂). Если y₂ > x₂, то (dP/dx₂) > 0, что и требовалось доказать.

С учетом вышеизложенного первый закон Гиббса-Коновалова может быть сформулирован и так: общее давление пара над ра-ром растёт с ростом доли в ра-ре того компонента, который богаче представлен в паре (более летучего компонента).

Второй закон Гиббса-Коновалова касается более частных случаев и выполняется для реальных ра-ров с большими отклонениями от закона Рауля, на кривых «общее давление пара – состав» для которых имеются минимумы или максимумы. Второй закон Гиббса-Коновалова гласит: максимум на кривой общего давления соответствует минимуму на кривой температур кипения и отвечает такому равновесию ра-ра и насыщенного пара, при котором составы фаз одинаковы, и наоборот.

Экстремумы на кривой зависимости общего давления насыщенного пара от состава ра-ра удовлетворяют условию (dP/dx₂) = 0, а в соответствии с уравнением (8.39) это возможно, только если в этих точках y₂ = x₂. Итак, в экстремумах общего давления пара (или температур кипения) ра-р и насыщенный пар имеют одинаковый состав.

Возможные диаграммы состояния бинарных систем с максимумом на кривой давления пара и минимумом на кривой температур кипения представлены на рис. 8.7.

Р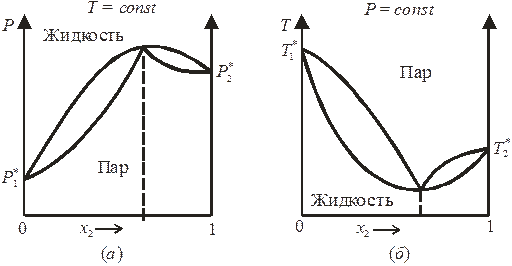 ис. 8.7. Диаграммы состояния бинарных систем с максимумом на кривой давления пара (а) и минимумом на кривой температур кипения (б).

Смеси, у которых ра-р и пар одинаковы по составу, называются азеотропными, или нераздельнокипящими. Путём перегонки азеотропные ра-ры не разделяются (составы фаз равны). Но их можно разделить следующими методами: — путём химического связывания одного из компонентов; — путем добавления в систему третьего компонента;— путем ректификации на двух последовательных колонках при различных давлениях. Примерами азеотропных смесей с минимумами на кривых температур кипения являются ра-ры, содержащие Н₂О и С₂Н₅ОН (96,5%), метанол и ацетон. Примерами азеотропных смесей с максимумами на кривых кипения являются ра-ры, содержащие Н₂О и НСl (20%), ацетон и хлороформ.

Т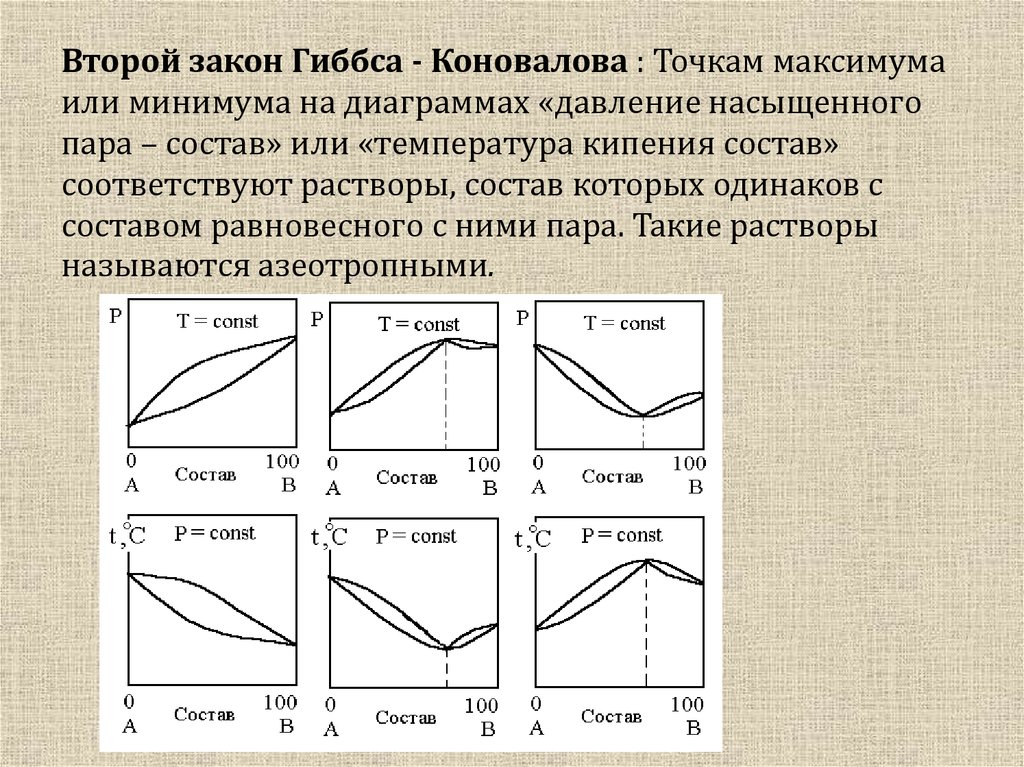 ретий закон Гиббса-Коновалова гласит: в изотермических или изобарических условиях состав насыщенного пара и состав жидкого ра-ра меняются синбатно (составы обеих фаз меняются в одном направлении). Данный закон логично следует из изученного материала и для его обоснования достаточно еще раз внимательно изучить диаграммы состояния, представленные, например, на рис. 8.3 – 8.5. Второй закон Гиббса-Коновалова: точка максимума или минимума на диаграммах «давление насыщенного пара-состав» или «температура кипения-состав» соответствуют ра-ры, состав которых одинаков с составом равновесного с ним пара. Такие ра-ры называют азеотропными. Равновесие ж-пар в двухкомпонентных системах Если при образовании ра-ра не происходит изменение объема (V=0) и энтальпии системы (H=0), то такой ра-р называется идеальным. Идеальные ра-ры образуются тогда, когда исходные компонента близки по свойствам (смеси изотопов, гомологов и т.п.). Во всем интервале концентрации ра-ритель А и ра-ренное вещество В идеального ра-ра подчиняются закону Рауля: (7.1) (7.2) где, P_A и Р_В – парциальные давления паров летучих компонентов А и В над ра-ром. и - давление паров над чистыми компонентами. и - молярные доли этих компонентов в ра-ре ( + =1). При невысоких давлениях пар можно считать смесью идеальных газов. Тогда, согласно закону Дальтона, общее давление пара над идеальным ра-ром будет равно сумме парциальных (частичных), давлений пара компонентов: (7.3)

З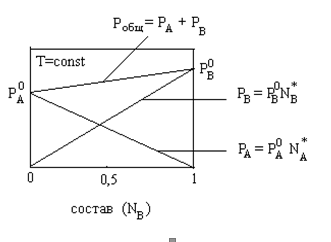 ависимость общего и парциального давлений пара от состава идеального ра-ра показано на рис. 7.1.

В большинстве случаев состав пара отличается от состава жидкого ра-ра, из которого он получен. Если пар подчиняется законам идеальных газов и находится в равновесии с идеальным ра-ром , то его состав можно найти, зная состав жидкого ра-ра:

; (7.4)

На практике имеют дело с неидеальными ра-рами, имеющими отклонения от идеальности, которые вызываются как физическими, так и химическими величинами (дипольные взаимодействия, поляризация, образования водородных связей, ассоциация, диссоциация, сольватация и др.). Отклонения могут быть положительными и отрицательными.

В ра-рах с положительными отклонениями от идеальности (рис. 7.2). U>0. Образование таких ра-ров сопровождается поглощением теплоты и увеличением объема. Рис.7.2 В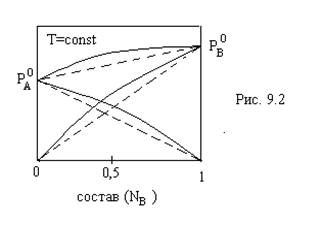 ра-рах с отрицательным отклонением от идеальности U<0. Образование таких ра-ров сопровождается выделением теплоты и уменьшением объема. (рис.7.3)

Д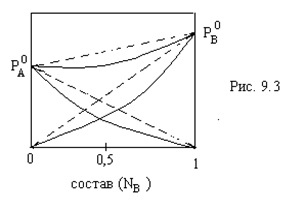 ля неидеального ра-ра состав пара находиnся не по уравнению (7.4), а экспериментальным путем. Для изучения равновесия пар-жидкий ра-р применяют два типа диаграмм состояния: 1) диаграммы давления пара-состав (Т=const) и 2) диаграммы температура кипения-состав (P=const). Чаще пользуются вторыми диаграммами. Разные виды диаграмм даны на рис. 7.4.

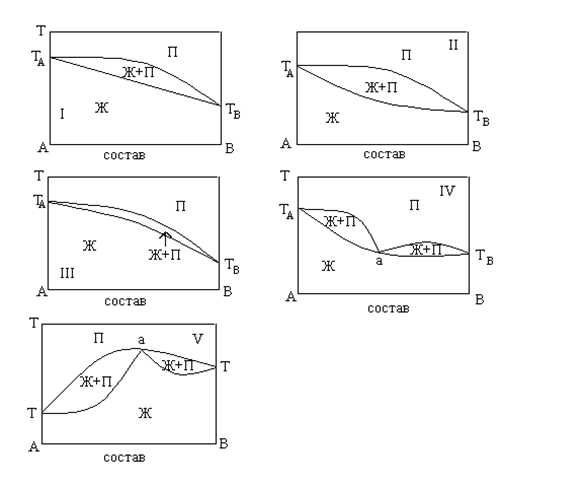Диаграммы кипения бинарных систем (изобары, Р=const):

I – идеальный ра-р;

II – неидеальный ра-р с незначительным положительным отклонением;

III – неидеальный ра-р с незначительным отрицательным отклонением;

IV - неидеальный ра-р со значительным положительным отклонением;

V - неидеальный ра-р со значительным отрицательным отклонением от закона Рауля.

На этих диаграммах фигуративные точки T_A и T_B изображают температуры кипения чистых компонентов при данном внешнем давлении P. Каждая из диаграмм кипения имеет две кривые, разделяющие диаграмму на три области:

1) Область пара (П) 2) Область жидкости (Ж) 3) Область равновесия пара и жидкости ( ).

Число степеней свободы соответственно равно: С₁=2-1+1=2 С₂=2-1+1=2 С₃=2-2+1=1

Фигуративные точки, лежащие на нижней кривой, характеризуют составы кипящих жидкостей и температуры при которых начинают кипеть жидкости заданного состава при данном давлении Р. Фигуративные точки, лежащие на верхней кривой, характеризуют составы насыщенного пара и температуры, при которой исчезают последние капли жидкости при кипении исходных смесей.

Характерной особенностью неидеальных ра-ров со значительным положительным или отрицательным отклонениями от закона Рауля является их способность образовывать азеотропные смеси, которые на диаграммах состояния изображена точкой а.

Азиотропные смеси – это ра-ры при испарении которых получается пар того же состава, что и исходная жидкая смесь. На диаграммах появляются экстремальные точки а.

Поскольку азеотропные смеси кипят при данном внешнем давлении при постоянной температуре ,как и чистые вещества ,то правило фаз для них рассчитывается так:

С=2-2+1-1=0

По диаграммам состояния можно определять качественные и количественные состава равновесных фаз. Рассмотрим диаграмму (Рис. 7.5.).

Д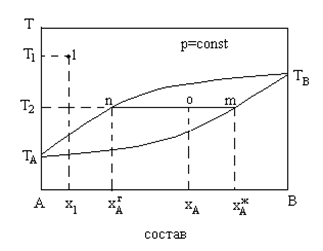 иаграмма кипения системы для азеотропной смеси.

Точка 1 – фигуративная точка, отвечающая составу Х₁. Отрезок АХ₁ определяет массовую долю компонента В в данной системе, а отрезок ВХ₁ – массовую долю компонента А. Внутри «линзы» система имеет гетерогенность. Точка О отвечает составу Х_А. При проведении соединительной прямой (ноды) получаем точки n и m, проекции которых на горизонтальную ось дают составы парообразной и жидкой фаз соответственно.

Для определения количественных соотношений между фазами применяют «правило рычага». Для точки О масса системы m=m^*+m^П. Из уравнения mx_A=m^* +m^П+m ,

выражающего распределение вещества А между жидкой и парообразными фазами получаем: (7.5) Масса равновесных фаз обратно пропорционально отрезкам, но которые делит ноду фигуративная точка гетерогенной системы.

Бинарные системы с образованием эвтектики с тв ра-рами, с конгруэнтной и инкогруэнтной tпл. Диаграмма состояния системы с эвтектикой. Наиболее проста диаграмма состояния системы, в которой компоненты неограниченного смешиваются в жидком состоянии, совершенно не смешиваются в твердом, химически не взаимодействуют друг с другом и не образуют твердых ра-ров. Образование таких диаграмм наблюдается, как правило, в том случае, когда компоненты А и В имеют разные типы кристаллических решеток и различные размеры радиусов частиц решетки, или при наличии одинакового типа решетки резко различных радиусов частиц. Диаграмма состояния системы с простой эвтектикой для компонентов А и В схематически представлена на рис.2

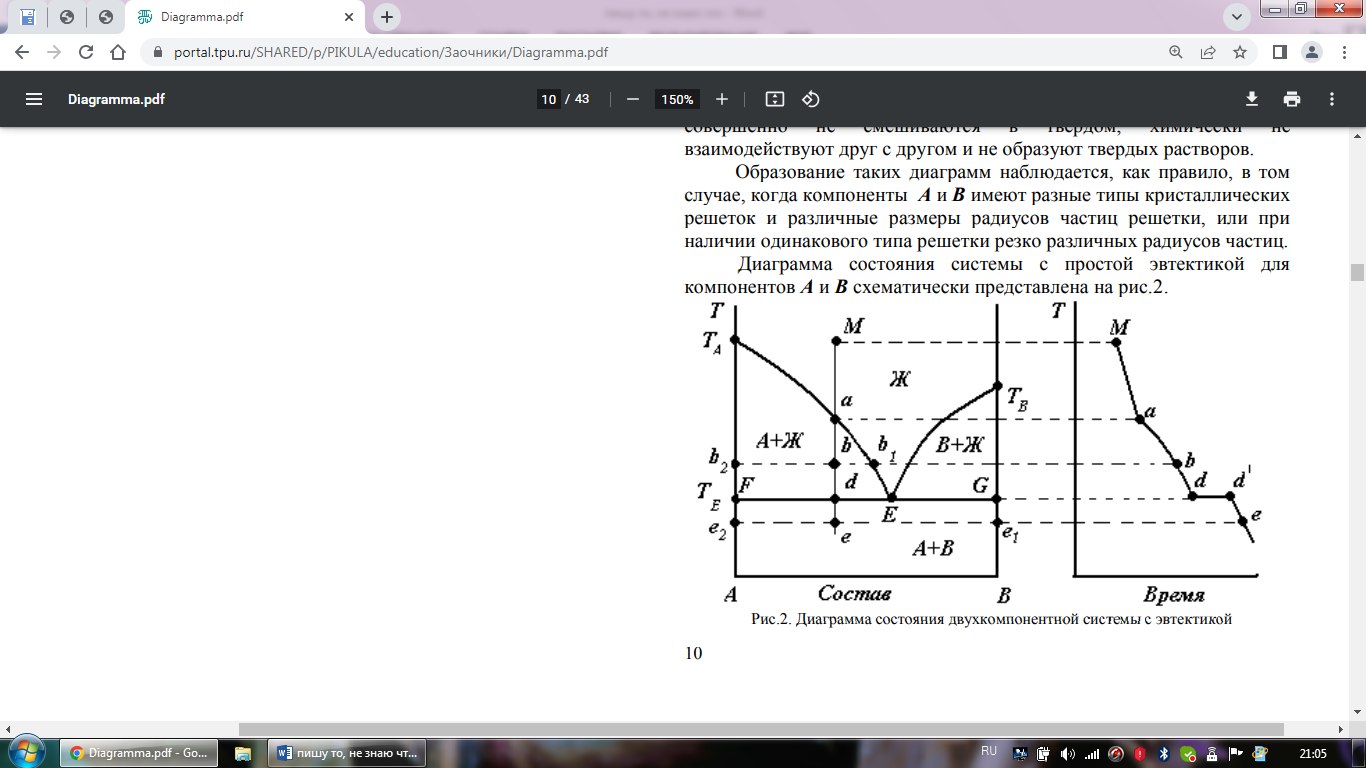
Эвтектика – механическая смесь кристаллов двух компонентов, обладающая самой низкой температурой кристаллизации (плавления).

Фазовая диаграмма с конгруэнтно плавящимся химическим соединением Если компоненты А и В образуют одно устойчивое химическое соединение состава АхВy , плавящееся без разложения, то на диаграмме состояния кривая ликвидуса образует максимум в точке Д (рис.4). В этой точке состав кристаллической фазы совпадает с составом жидкой фазы. В случае, если максимум на диаграмме имеет острую форму, химическое соединение АВ устойчиво при плавлении; если максимум «пологий», то химическое соединение частично диссоциирует при плавлении. Как видно из рис.4, фазовая диаграмма представляет собой как бы две диаграммы с простой эвтектикой: А-АВ и В-ВА. Можно разделить такую диаграмму на две части по вертикали, соответствующей химическому соединению, и рассматривать каждую часть диаграммы отдельно.

Диаграммы с конгруэнтно плавящимися химическими соединениями образуют системы: Ca-Mg, Mg-Pb, Mg-Sn, NaF-AlF3.

Ф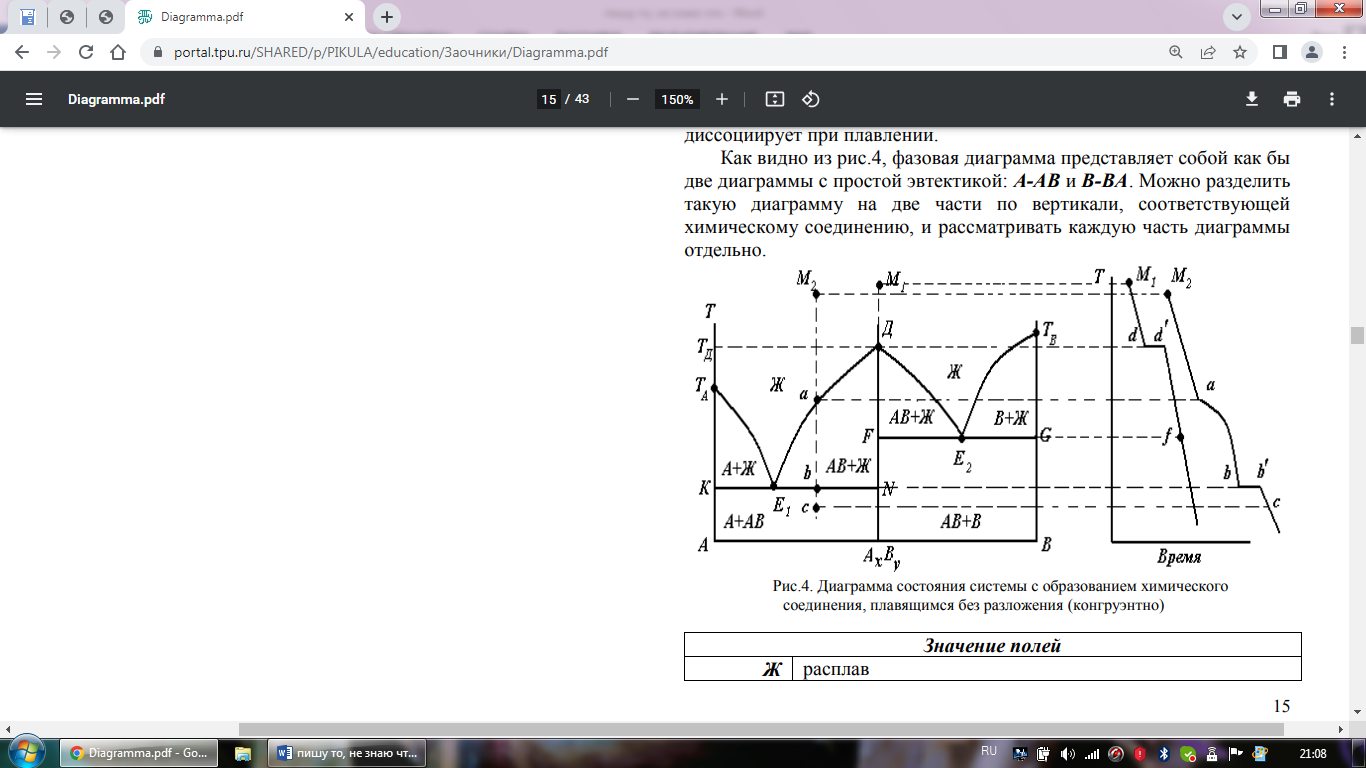 азовая диаграмма с инконгруэнтно плавящимся химическим соединением

Диаграмма, когда компоненты А и В могут образовывать химическое соединение АхВy, плавящееся с разложением, т.е. инконгруэнтно, приведена на рис.5.

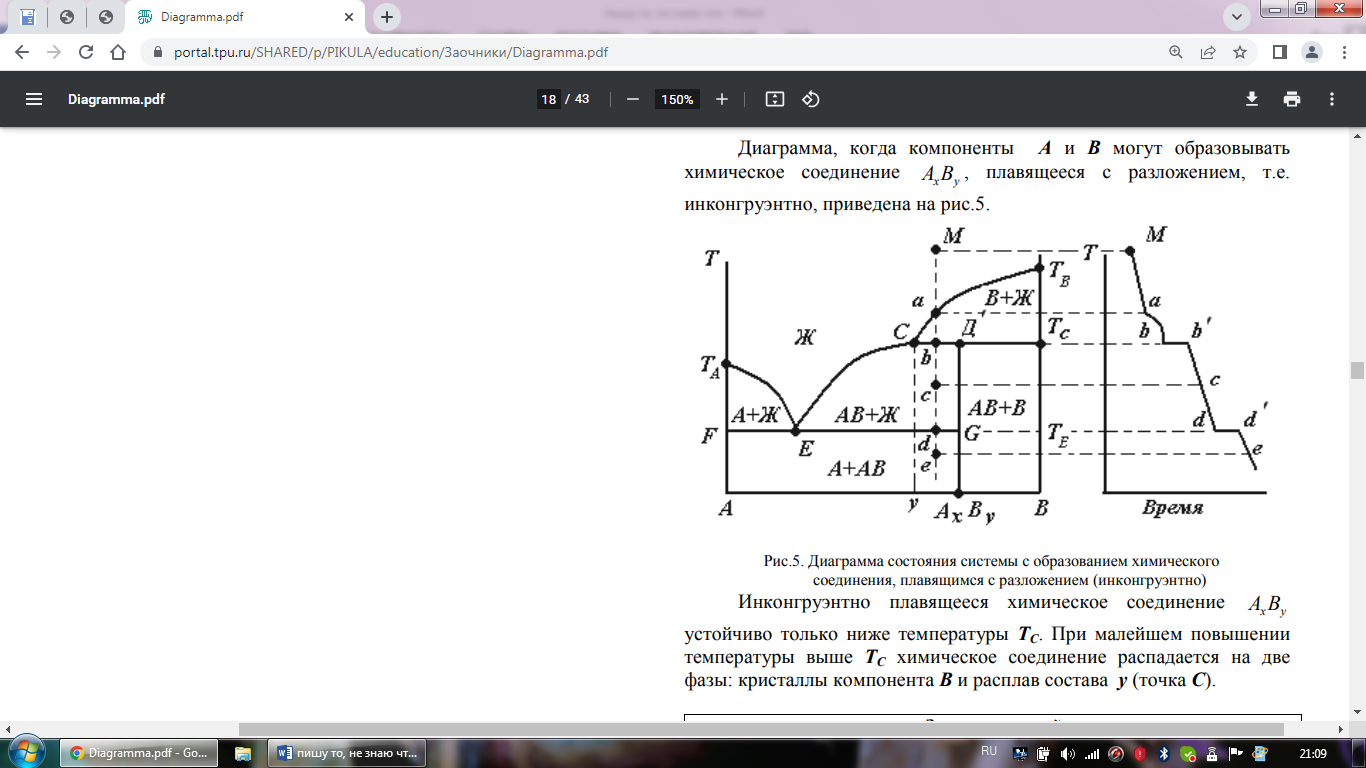Инконгруэнтно плавящееся химическое соединение АхВy устойчиво только ниже температуры ТС. При малейшем повышении температуры выше ТС химическое соединение распадается на две фазы: кристаллы компонента В и расплав состава y (точка С).

Диаграммы с инконгруэнтно плавящимися химическими соединениями образуют системы: Al2O3 - SiO2, CaSiO3 - BaSiO3, Fe - P, Li - Sn и др.

Твердые ра-ры – гомогенные системы переменного состава, состоящие из двух или более компонентов.

Ф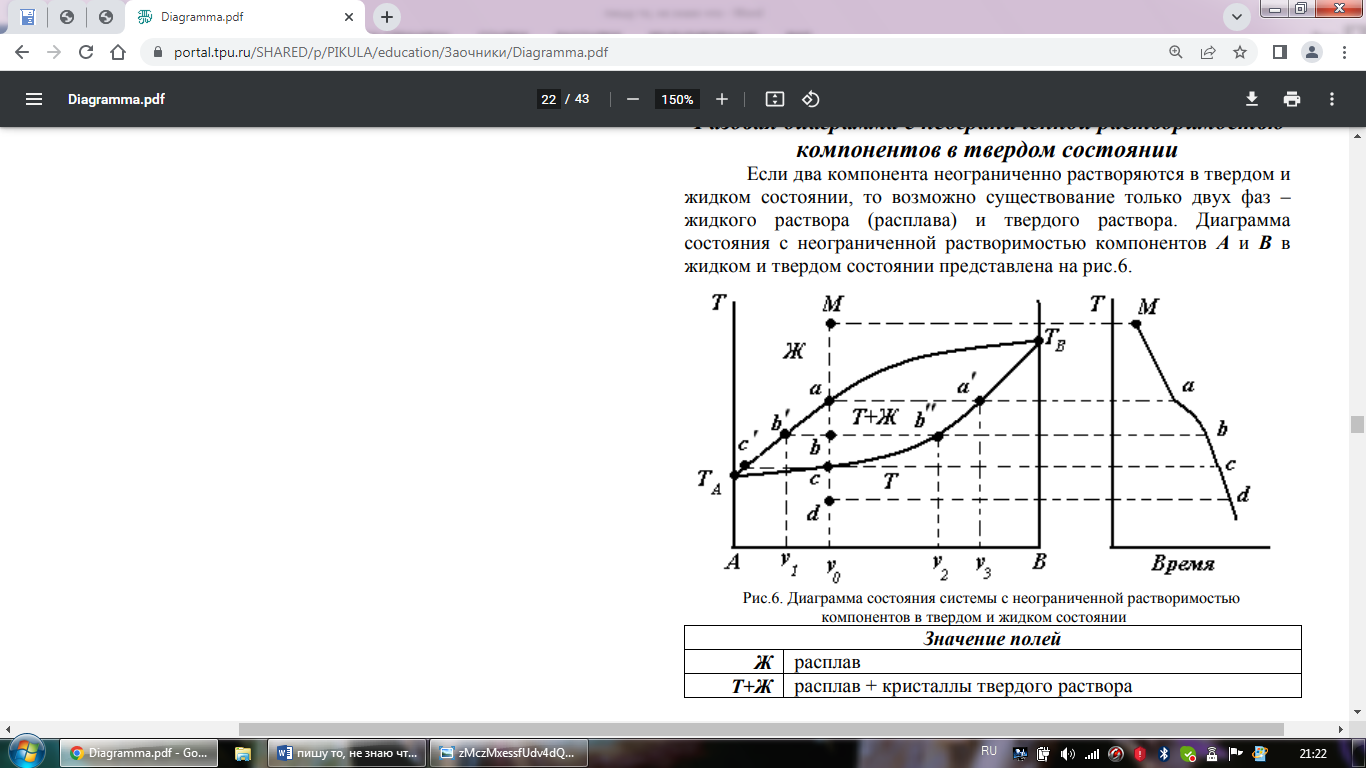 азовая диаграмма с неограниченной ра-римостью компонентов в твердом состоянии

Если два компонента неограниченно ра-ряются в твердом и жидком состоянии, то возможно существование только двух фаз – жидкого ра-ра (расплава) и твердого ра-ра. Диаграмма состояния с неограниченной ра-римостью компонентов А и В в жидком и твердом состоянии представлена на рис.6.

Фазовые диаграммы с ограниченной ра-римостью компонентов в твердом состоянии

Различают два типа диаграмм: 1.Диаграмма с эвтектикой (I типа) – твердые ра-ры образуют эвтектическую смесь. 2.Диаграмма с перитектикой (II типа) – твердые ра-ры образуют перитектическую смесь (один из твердых ра-ров устойчив только до определенной температуры).

Диаграммы состояния с ограниченной ра-римостью компонентов с эвтектикой (I типа)

В такой системе не образуются фазы, представляющие собой чистые компоненты. Из расплава могут кристаллизоваться только твердые ра-ры α или β.

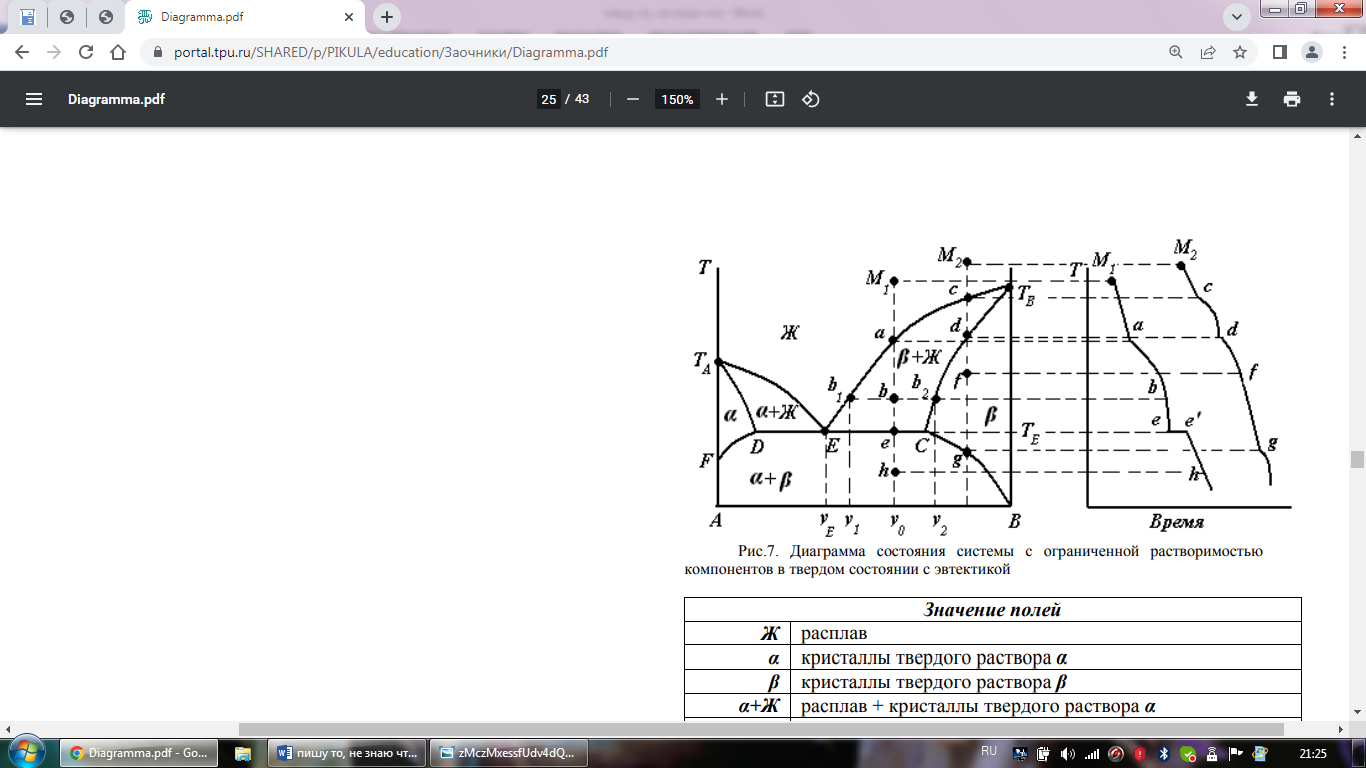Диаграммы состояния с ограниченной ра-римостью компонентов с перитектикой (II типа)

Рассмотрим фазовую диаграмму образования твердых ра-ров с ограниченной ра-римостью компонентов и с образованием перитектической смеси (рис.8).

Расчеты выходов продуктов для неидеальных систем

Д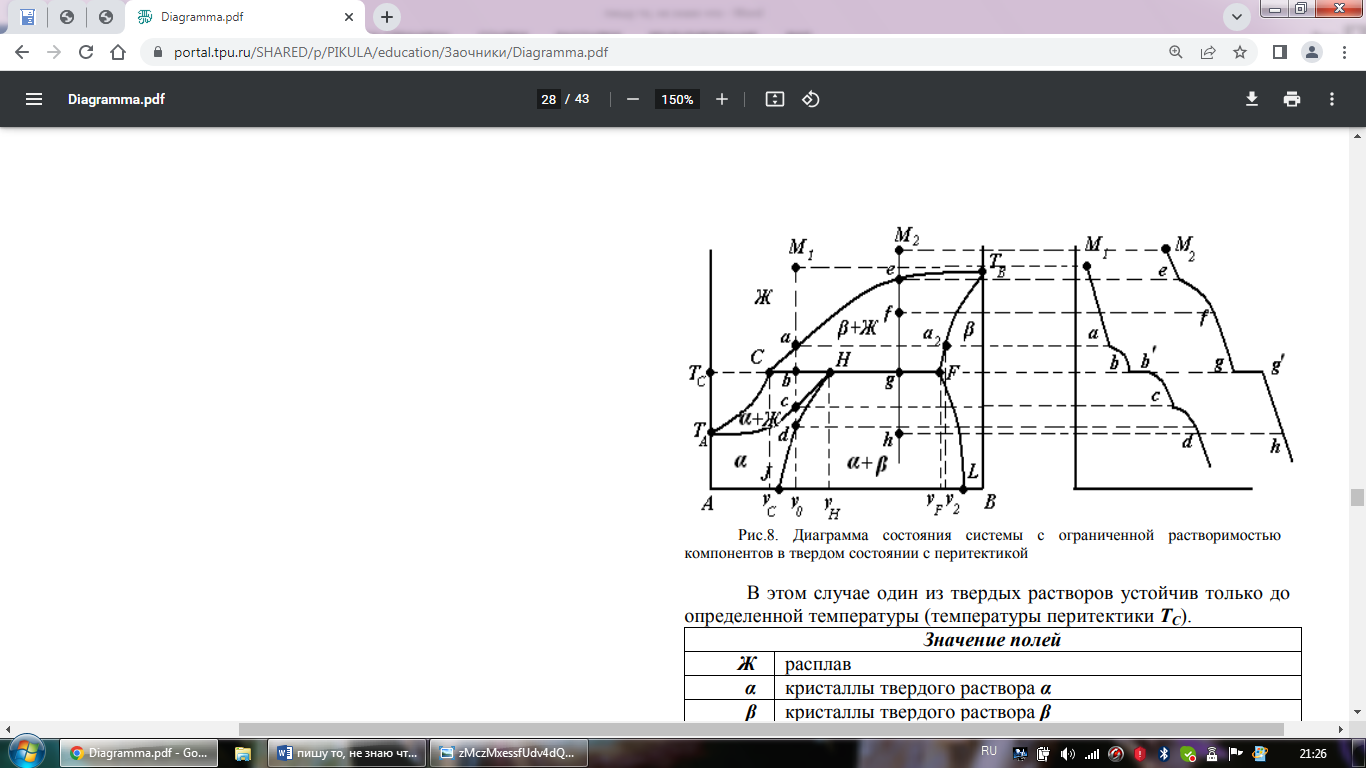 ля расчета равновесного состава была введена универсальная величина – химическая переменная или глубина превращения ξ (кси), равная отношению изменения количества вещества данного реагента или продукта реакции к его стехиометрическому коэффициенту в уравнении химической реакции:

 ,

где знак “+” используется для продуктов реакции, а знак “ – “ для исходных веществ.

Равновесное количество вещества для каждого участника реакции выразим через глубину превращения:

Подставив полученное выражение в уравнение, связывающее термодинамическую K_a = и практическую K_n константы равновесия, получим

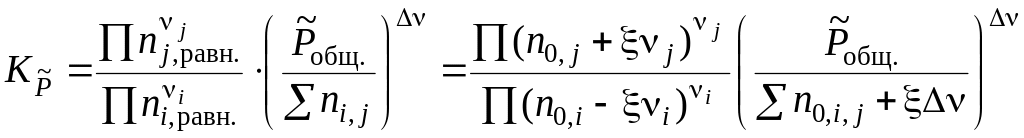
Решив это уравнение относительно химической переменной ξ, можно рассчитать: равновесные количества вещества каждого участника реакции, равновесные концентрации реагентов, степень превращения исходных веществ и выход продуктов реакции.

Зависимость выхода от природы инертного ра-рителя

Инертные ра-рители не способны отдавать протоны, они также не способны изменять основных, кислых или амфотерных свойств химических соединений, которые в них ра-рены. К группе углеводных ра-рителей относятся углеводороды и их галогенопроизводные. Инертные ра-рители применяют для того, чтобы замедлить скорость присоединения. Но есть жидкости, например, ледяная уксусная кислота, которые применяют в качестве ра-рителя. В ней отлично ра-ряются бромистый и хлористый водород.

Также инертные ра-рители применяются для смол, у которых плохая вязкость. В природе существуют инертные ра-рители, которые не проявляют своих основных или кислотных свойств – это диоксан, гексан, диоксан, бензол, ацетон и хлороформ. Инертные ра-рители помогают выделяться продуктам нейтрализации в форме кристаллов. Это очень помогает при титровании, потому что помогает усиливать четкость цветовых переходов на индикаторе, к примеру, когда отделятся сульфамиды.

Идеальные жидкие ра-ры и их св-ва. Под идеальным обычно понимают ра-р, для компонентов которого при всех составах и температурах выполняется закон Рауля. Согласно закону Рауля,

Давление пара ра-рителя p_i над ра-ром пропорционально мольной доле ра-рителя x_i в ра-ре: p_i =

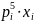
Для бинарного ра-ра закон Рауля можно представить в следую щем виде: 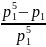= 1 – x₁ = x_2, то есть относительное понижение давления пара ра-рителя над рас- твором равно мольной доле x₂ ра-ренного вещества.

Общее давление пара над ра-ром равно сумме парциальных дав- лений p₁ и p₂: p = p₁ + p₂ = 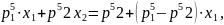то есть давление пара линейно зависит от состава ра-ра.

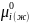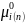Закон Рауля и его т/д вывод При равновесии химический потенциал вещества одинаков во всех существующих фазах. Очевидно, хим. Потенциал компонента жидкого ра-ра μ_i(Ж) будет равен химическому потенциалу пара этого компонента μ_i(П) над ра-ром: μ_i(Ж)= μ_i(П). Подставляем уравнения химических потенциалов идеальных ра-ров + RTln x_i = + RTln p_i

Давление пара вещества над чистым ра-рителем равно Р⁰_i, поэтому при х_i=1 (чистое вещество) уравнение переходит в = + RTln p⁰_i

Подстановка соотношения (2) в (1) дает + RTln p⁰_i + RTln x_i = + RTln p_i. Откуда после небольших упрощений получается уравнение р₁=р⁰₁х₁

Если ра-р состоит из 2-х летучих компонентов. А пар обладает свойствами идеального газа, то закон Рауля будет справедлив как для р-ля, так и для ра-ренного вещества: р₁=р⁰₁х₁ (3); Р₂=р⁰₂х₂ (4)