15. Плоское движение твердого тела. Скорости точек плоской фигуры. Ускорения точек плоской фигуры.

http://botva-project.ru/library/%D0%9F%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5.pdf

Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется  в плоскости, параллельной некоторой неподвижной плоскости

Рассмотрим методы, с помощью которых можно определить скорости точек тела, совершающего плоское движение.

+1. Метод полюса. Этот метод основывается на полученном разложении плоского движения на поступательное и вращательное. Скорость любой точки плоской фигуры можно представить в виде двух составляющих: поступательной, со скоростью равной скорости произвольно выбранной точки – полюса, и вращательной вокруг этого полюса

Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

Ускорения точек плоской фигуры

Формула распределения ускорений при плоском движении тела имеет вид:

где   - ускорение полюса, точки  , в поступательном движении;

 - относительное ускорение точки   в ее вращательном движении вместе с телом вокруг полюса  ;

 - ускорение любой точки   тела.

Ускорение любой точки   плоской фигуры равно геометрической сумме ускорения точки, которую выбрано за полюс, и ускорения точки   при его вращении вместе с телом вокруг этого полюса.

Графическое определение ускорения точки   выполняется следующим образом (рис.4.16):

• Из точки   откладывают вектор  , который равен ускорению полюса  ;

• Под углом   к   проводят вектор  , отклоненный в сторону углового ускорения  , причем

• Модуль и направление ускорения   определяется диагональю параллелограмма, который построен на векторах   и   как на сторонах.

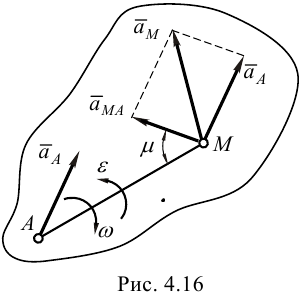
Вычисление величины ускорения точки   с помощью рассматриваемого параллелограмма затрудняет расчеты, поскольку предварительно надо определить угол между векторами   и  .

Учитывая, что  представляет собой относительное ускорение точки   в ее относительном вращательном движении вокруг полюса  , то это ускорение можно разложить на относительную тангенциальную (касательную) и относительную нормальную (центростремительную) составляющие:

где

Вектор   направлен перпендикулярно   в сторону углового ускорения, а вектор   всегда направлен от точки   к выбранному полюсу   (рис.4.17).

Тогда уравнение (4.10) примет вид:

Если точка  , которая выбрана за полюс поступательного движения, движется не прямолинейно, то ее ускорение, в свою очередь, тоже можно разложить на тангенциальную   и нормальную   составляющие:

Было отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью   полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически  из скоростей, которые точка получает в каждом из этих движений.

В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором   (рис.3), где  - радиус-вектор полюса А,  - вектор, определяю­щий положение точки М  относительно осей  , перемещающих­ся вместе с полюсом А поступательно (движение фигуры по отноше­нию к этим осям представляет собой вращение вокруг полюса А). Тогда

В полученном равенстве величина   есть скорость полюса А; величина же   равна скорости  , которую точка М получает при  , т.е. относительно осей  , или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что

.

Скорость  , которую точка М получает при вращении фигуры вокруг полюса А:

,

где ω - угловая скорость фигуры.

Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление скорости   находятся построением соответствующего параллело­грамма (рис.4).

                                      

Рис.3                                                               Рис.4