4. Теорема о трех силах. Примеры.

Теорема. Если свободное абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, лежащих на одной плоскости, то линии действия этих сил пересекаются в одной точке.

Доказательство.

Пусть на абсолютно твердое тело, находящееся в равновесии действуют три непараллельные силы F⃗ 1F→1, F⃗ 2F→2 и  F⃗ 3F→3 как указано на рис. С.17а.

       В соответствие со следствием аксиомы №2 силы  F⃗ 1F→1 и F⃗ 2F→2  являются скользящими векторами и их можно перенести вдоль линии действия в точку их пересечения  OO. Теперь силы  F⃗ 1F→1 и F⃗ 2F→2 приложены к одной точке и в соответствие с аксиомой №3 их можно сложить R⃗ =F⃗ 1+F⃗ 2R→=F→1+F→2.

Теперь, как следует из рис.С.17б  тело находится в равновесии под действием системы состоящей из двух сил {F⃗ 3,R⃗ }{F→3,R→} и в соответствие с аксиомой №1 эти силы действуют вдоль одной прямой. Следовательно, линии действия сил F⃗ 1F→1 , F⃗ 2F→2 и F⃗ 3F→3 имеют общую точку пересечения, точку OO и образуют сходящуюся систему сил.

Пример.

Стержень  ABAB в точке  AA опирается на неподвижный шарнир, а в точке CC на выступ (рис.С.18).

 

Определить направления реакций в опорах (точках  AA  и CC).

Решение.

Решение приведено графически на рис.С.19.

 

5. Связи. Реакции связей. Основные типы реакций связей. Примеры.

По определению, тело, которое может совершать из данного по­

ложения любые перемещения в пространство, называется свободным

(например, воздушный шар в воздухе). Тело, перемещениям кото­

рого в пространстве препятствуют какие-нибудь другие, скреплен­

ные или соприкасающиеся с ним, тела, называется несвободным.

Все то, что ограничивает перемещения данного тела в пространстве,

называют связью.

Связями будем называть все тела, которые ограничивают перемещение данного тела.

Сила, с которой данная связь действует на тело, называется реакцией связи.

1. Гладкая поверхность.

Р еакция гладкой поверхности перпендикулярна этой поверхности.

2. Невесомый стержень.

Р еакция стержня всегда направлена вдоль его оси. Стержень может работать и на сжатие и на растяжение.

3. Неподвижный цилиндрический шарнир.

Ка к правило, направление реакцииR_A заранее не известно, поэтому ее раскладывают по двум известным направлениям, например, по направлению координатных осей.

4. Подвижный цилиндрический шарнир.

Р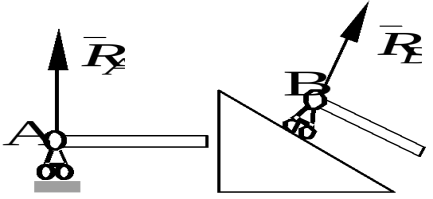 еакция перпендикулярна плоскости возможного перемещения шарнира.

5. Жесткая заделка.

Реакция в данном случае состоит из трех компонентов: двух составляющих силы X_A, Y_A и реактивного момента M неизвестного направления (понятие момента силы будет рассмотрено позже).

6. Скользящая заделка.

+Ре акция включает силу, перпендикулярную оси заделки, и реактивный момент.

Пример.

Брус DE закреплен в точке D неподвижным шарниром, а в точке Е опирается на гладкую поверхность стены (рис.С.12а).

 

Для бруса DE связями служат два тела: неподвижный шарнир D и гладкая поверхность стены.

Раскладываем реакцию неподвижного шарнира на две составляющие  X⃗D→D и  Y⃗D→D и показываем на чертеже предполагаемые направления этих составляющих.

Реакция гладкой стены приложена в точке Е касания балки и стены и направлена по нормали к стене (рис.С.12б).

На рис.С.13 приведен также пример использования опирания на неподвижный шарнир и гладкий выступ.