Матан вопросы

1. Дайте определение линейных однородных и неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами

2. Дайте понятие характеристического уравнения

3. Укажите три возможных вида решения ЛОДУ в зависимости от корней характеристического уравнения

4. Опишите, как найти общее решение ЛНДУ

1. Перечислите виды дифференциальных уравнений, допускающих понижение порядка

Понижение порядка уравнения, не содержащего y и y'

Понижение порядка уравнения, не содержащего y

Понижение порядка уравнения, не содержащего x

2. Сформулируйте алгоритмы решения каждого вида дифференциальных уравнений, допускающих понижение порядка

Понижение порядка уравнения, не содержащего y и y'

Это дифференциальное уравнение вида  . Произведём замену переменной: введём новую функцию   и тогда  . Следовательно,   и исходное уравнение превращается в уравнениие первого порядка

с искомой функцией  .

Решая его, находим  . Так как  , то  .

Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где   и   - произвольные константы интегрирования.

Понижение порядка уравнения, не содержащего y

Это дифференциальное уравнение вида  . Произведём замену переменной как в предыдущем случае: введём  , тогда  , и уравнение преобразуется в уравнение первого порядка  . Решая его, найдём  . Так как  , то  . Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где   и   - произвольные константы интегрирования.

Понижение порядка уравнения, не содержащего x

Это уравнение вида  . Вводим новую функцию  , полагая  . Тогда

.

Подставляя в уравнение выражения для   и  , понижаем порядок уравнения. Получаем уравнение первого порядка относительно z как функции от y:

.

Решая его, найдём  . Так как  , то  . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:

,

где   и   - произвольные константы интегрирования.

1. Какие дифференциальные уравнения называют линейными

Дифференциальные уравнения вида y⁽ⁿ⁾ + p₁(x) у^(n-1) + ... + p_n(x)y = f(x), где у = y(x) — искомая функция, y⁽ⁿ⁾, у^(n-1),..., y' — её производные, a p₁(x), p₂(x),..., p_n(x) (коэффициенты) и f(x) (свободный член) — заданные функции.

2. Что называется фундаментальной системой решения линейных дифференциальных уравнений

Фундаментальной системой решений линейного однородного дифференциального уравнения n-го порядка называется любая линейно независимая система y₁(x), y₂(x), …, y_n(x) его n частных решений.

3. Сформулируйте задачу Коши для дифференциальных уравнений высших порядков

Задача, в которой требуется найти частное решение дифференциального уравнения

 ,

удовлетворяющее заданным начальным условиям

 ,

 ,

 ,

…………..

 ,

называется задачей Коши или начальной задачей для дифференциального уравнения высшего (n-го) порядка.

4. Чем отличается внешний вид однородного и неоднородного линейного дифференциального уравнения высшего порядка

Линейным дифференциальным уравнением высшего (n-го) порядка называется уравнение, линейное относительно неизвестной функции   и ее производных

 .

Если   , то уравнение называется линейным однородным уравнением или уравнением без правой части.

Если же   , то уравнение называется линейным неоднородным уравнением или уравнением с правой частью.

1. Перечислите виды дифференциальных уравнений первого порядка

Простейшие дифференциальные уравнения первого порядка вида 

Дифференциальные уравнения с разделяющимися переменными вида   или 

Линейные неоднородные дифференциальные уравнения первого порядка 

Дифференциальное уравнение Бернулли 

Уравнения в полных дифференциалах 

2. Укажите виды дифференциальных уравнений первого порядка, которые решаются заменой переменных, запишите эти замены

Некоторые дифференциальные уравнения можно свести к уравнениям с разделяющимися переменными с помощью замены переменных.

Дифференциальные уравнения   приводятся к ОДУ с разделяющимися переменными подстановкой z = ax+by. К примеру, уравнение   с помощью подстановки z = 2x+3y приобретает вид  .

ОДУ   или   преобразуются к уравнениям с разделяющимися переменными с помощью замен   или  . Например, дифференциальное уравнение   после замены   принимает вид  .

Некоторые дифференциальные уравнения следует немного преобразовать, чтобы можно провести замену. К примеру, достаточно разделить на x² или y² числитель и знаменатель правой части дифференциального уравнения  , чтобы оно соответствовало случаям   или   соответственно.

Дифференциальные уравнения   преобразуются к только что рассмотренным ОДУ   или  , если ввести новые переменные  , где   - решение системы линейных уравнений   и провести некоторые преобразования.

Например, дифференциальное уравнение   после введения новых переменных   преобразуется к виду  . Проводим деление на u числителя и знаменателя правой части полученного уравнения и принимаем  . В результате приходим к уравнению с разделяющимися переменными  .

3. Сформулируйте алгоритм решения дифференциальных уравнений первого порядка

1. Дайте понятие криволинейной трапеции

Криволинейная трапеция – плоская фигура, ограниченная графиком неотрицательной непрерывной функции у = f(x), определенной на отрезке [a; b], осью абсцисс и прямыми х = а, х = b.

2. Расскажите, как определяется площадь криволинейной трапеции с помощью определенного интеграла в случае, когда функция, ограничивающая трапецию, не является неотрицательной

1. Разобьем отрезок  точками  на частичные отрезки.

2. В каждом отрезке  (где k=1, 2, ..., n) выберем произвольную точку  .

3. Вычислим площади прямоугольников, у которых основания есть отрезки  оси абсцисс, а высоты имеют длины  . Тогда площадь ступенчатой фигуры, образованной этими прямоугольниками, равна  .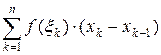

Заметим, что чем меньше длины частичных отрезков, тем более ступенчатая фигура по расположению близка к данной криволинейной трапеции.

3. В чем отличие в нахождении объемов тел вращения, полученных при вращении функции относительно осей ох и оу