
Ряды
.pdf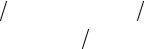
на множестве {x}, то множество занумерованных функций f1(x), f2(x), …, fn(x), … называется функциональной последовательностью.
Определение 13
Отдельные функции fn(x) называются членами (элементами) функциональной последовательности.
Определение 14
Множество {x}, на котором определены функции fn(x), называется областью определения функциональной последовательности.
Следует заметить, что если область определения {x} является множеством в m- мерном пространстве, то каждая функция fn(x) является функцией m переменных fn(x)=fn(x1,x2,…,xm), где x1,x2,…,xm – координаты точек x.
Определение 15 Формально записанную сумму
f1(x)+ f2 (x)+... + fn (x)+... = |
∞ |
∑ fn (x) |
|
|
n=1 |
бесконечного числа членов функциональной последовательности, которая называется функциональным рядом. При этом отдельные функции fn(x) называются членами ряда, а множество {x}, на котором определены эти функции, называется область определения функционального ряда.
Определение 16
Сумма первых n членов функционального ряда называется n-ой частичной суммой этого ряда Sn(x).
Пример 8
Рассмотрим последовательность функций {fn(x)}, каждая из которых определена на сегменте 0≤x≤1 и имеет вид
fn (x)= cos (π n x 2), |
0 ≤ x ≤1 n |
|
|
0, |
1 n < x ≤1 |
На рис. 1 приведены графики функций f1(x), f2(x) и fn(x). Областью определения данной последовательности является сегмент 0≤x≤1. Следует заметить, что каждая функция fn(x) непрерывна на сегменте 0≤x≤1.
Пример 9 Рассмотрим степенной ряд
∞ |
(x + y)n |
=1+ |
x + y |
+ |
(x + y)2 |
+... + |
(x + y)n |
+..., |
|
∑ |
n! |
|
|
n! |
|||||
1 |
2! |
||||||||
n=0 |
|
|
|
|
областью определения которого является плоскость {-∞<x<+∞,-∞<y<+∞}. Может быть показано, что суммой данного ряда является следующая функция
ex+y = |
∞ |
(x + y)n |
. |
∑ |
n! |
||
|
n=0 |
|
9
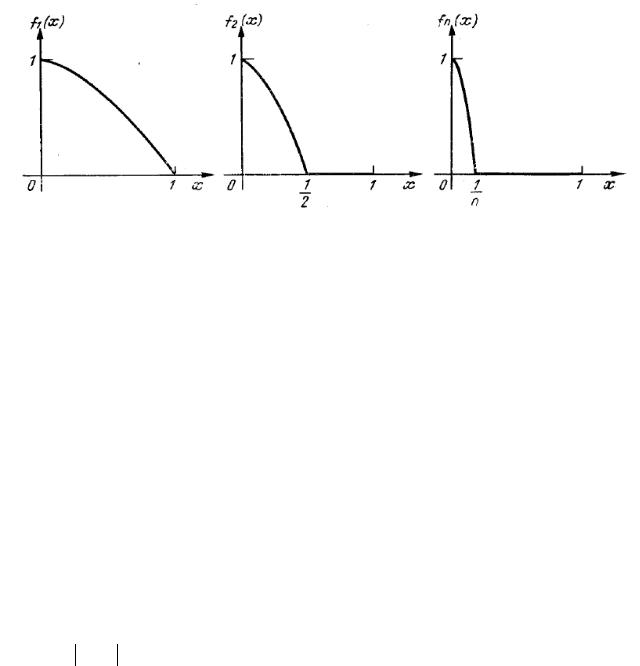
Рис. 1.
Определение 9
Последовательность функций f1(x), f2(x), …, fn(x), называется ограниченной, если существует такая постоянная M, что для всех x выполняется неравенство |fn(x)|≤M. Иногда такая последовательность называется равномерно ограниченной.
Определение 10
Последовательность действительных функций f1(x), f2(x), …, fn(x), называется убывающей (возрастающей), если выполняется неравенство fn+1(x)≤fn(x) (fn+1(x)≥
fn(x)).
Определение 11
Последовательность функций f1(x), f2(x), …, fn(x), называется сходящейся в точке x0, если сходится последовательность f1(x0), f2(x0), …, fn(x0).
Определение 12
Последовательность функций f1(x), f2(x), …, fn(x), называется сходящейся намножествеx, еслипоследовательностьсходитсявкаждой точкеэтого множества. Определение 13
Функциональный ряд ∑∞ fn (x) называется абсолютно сходящимся, если сходит-
n=1
∞ ( )
ся ряд ∑ fn x .
n=1
Определение 14
Пусть задана последовательность функций f1(x), f2(x), …, fn(x) и функция f (x). Данная последовательность сходится равномерно к функции f (x), если для любого ε>0 существует такой номер nε, что если n≥nε, то для всех x выполняется неравенство
|fn(x)-f(x)|< ε.
Свойства функциональных рядов
1) Степенной ряд
a0+a1x+a2x2+…+anxn+…
10

абсолютно сходится для всех значений x, по модулю меньших некоторого числа R (|x|<R, в качестве частного случая возможно R→∞), называемого радиусом сходимости степенного ряда. При |x|>R ряд расходится. Для ряда
a0+a1(x-x0)+a2(x-x0)2+…+an(x-x0)n+…
абсолютная сходимость имеет место при |x-x0|<R. При |x-x0|>R ряд расходится. Радиус может быть определён с помощью соотношений
R = lim 1 n an |
= lim an+1 an . |
n→∞ |
n→∞ |
Следует заметить, что на концах промежутка сходимости ряд может быть как сходящимся, так и расходящимся.
2) Существует только одно число R, которое является пограничным между областями сходимости и расходимости ряда.
∞ |
∞ |
3) Есди ряды ∑ fn (x) и |
∑ gn (x) сходятся равномерно в некоторой области, то |
n=1 |
n=1 |
для любых чисел λ и µ ряд ∞ [λ fn (x)+ µ gn (x)] также сходится равномерно в
∑
n=1
рассматриваемой области.
4) Если ряд ∑∞ fn (x) равномерно сходится в некоторой области, а функция g(x)
n=1
∞ |
|
|
|
|
|
|
|
ограничена, то ряд g (x)∑ fn (x) также сходится равномерно в рассматривае- |
|||||||
n=1 |
|
|
|
|
|
|
|
мой области. |
|
|
|
|
|
|
|
Пример 10 |
|
|
|
|
|
|
|
Рассмотрим степенной ряд |
|
|
|
|
|
|
|
1+ |
x |
+ |
x2 |
+... + |
xn |
+... |
|
1 |
2 |
n |
|||||
|
|
|
|
||||
Радиуссходимоститакогорядаравен R = lim (n +1) n =1. Такимобразом, ряд
n→∞
сходится абсолютно при -1<x<1. Рассмотрим точку x=-1. Полученный числовой ряд сходится условно. Рассмотрим точку x=1. Полученный числовой ряд расходится.
Теорема Абеля
Если степенной ряд при x0=0 сходится для положительного значания x =x1, то он сходится равномерно внутри промежутка x (-x1,x1). При этом его сумма S(x) является непрерывной в точке x1.
11
3. Ряд Тейлора
Определение 15
Пусть имеется функция f(x), дифференцируемая необходимое число раз на интервале её рассмотрения. Функция f(x) может быть представлена рядом Тейлора в окрестности точки x=a с помощью соотношения
f (x)= ∑∞ (x −a)n |
f (n)(a). |
n=0 n! |
|
Такой ряд может быть представлен в следующей форме
f (x)= ∑N (x −a)n |
f (n)(a)+ RN +1(x). |
n=0 n! |
|
Выделенная в отдельное слагаемое функция имеет вид
|
x −a p (x −ξ)N +1 |
|
(N +1)(ξ) |
|||
RN +1 |
(x)= |
|
|
n! p |
f |
|
|
||||||
|
x −ξ |
|
|
|||
иназывается остаточнымчленомвобщем виде. Возможны также и другие формы представления остаточного члена.
Определение 16
Частный случай ряда Тейлора, соответствующего разложению функции f(x) в окрестности точки x=0, т.е.
f (x)= |
∞ |
x |
n |
f (n)(0). |
|
∑ |
|
||||
n! |
|||||
|
n=0 |
|
|||
называется рядом Маклорена.
Некоторые разложения функций в ряд Маклорена
Пример 11
Разложим функцию f(x)=ex в ряд Маклорена. Такое разложение имеет следующий вид
ex =1+ |
|
x |
+ |
x2 |
+ |
x3 |
+... + |
xn |
+... = |
∞ |
xn |
. |
||
|
|
|
|
|
|
∑ |
|
|||||||
1! |
2! |
3! |
n! |
n! |
||||||||||
|
|
|
|
|
n=0 |
|
||||||||
Функции f(x)=ex, f(x)=1, f(x)=1+x, f(x)=1+x+x2/2, f(x)=1+x+x2/2+x3/6 представле-
ны на рис. 2 соответственно линиями 1, 2, 3, 4, 5.
12
20 |
|
|
|
|
|
|
1 |
|
|
5 |
|
10 |
|
4 |
|
|
|
3 |
|
|
2 |
|
|
0 |
|
|
|
0 |
1 |
2 |
3 |
|
|
Рис. 2. |
|
Пример 12
Разложим функцию f(x)=sin(x) в ряд Маклорена. Искомое разложение имеет следующий вид
sin (x)= x − |
x |
3 |
+ |
x |
5 |
− |
x |
7 |
+... +(−1)n+1 |
x |
2n−1 |
+... = |
∞ |
(−1)n+1 |
x |
2n−1 |
. |
||
|
|
|
|
|
∑ |
|
|
||||||||||||
|
|
|
|
|
|
(2n −1)! |
(2n −1)! |
||||||||||||
3! |
5! |
7! |
|
|
n=1 |
|
|
||||||||||||
Применение разложения функций в степенной ряд
Применение разложения функций в ряд Тейлора для вычисления пределов Для раскрытия неопределённостей, возникающих при вычислении пределов, может быть использовано разложение функций в ряд Тейлора.
Пример 13
Вычислим предел lim sin (x). Для его вычисления воспользуемся разложением
x→0 x
функции в ряд Маклорена. После подстановки рассмотренного в предыдущем примере разложения синуса в данный предел получаем
|
sin (x) |
|
|
1 |
∞ |
+ |
x2n−1 |
|
∞ |
(−1)n+1 |
||||
lim |
|
|
= lim |
|
∑(−1)n |
1 |
|
|
= |
∑ |
|
lim x2n−2 =1. |
||
x |
|
|
|
(2n −1)! |
|
|||||||||
x→0 |
|
|
x→0 x n=1 |
|
|
n=1(2n −1)! x→0 |
||||||||
Пример 14 |
|
|
|
ex −e |
|
|
|
|
|
|
|
|
||
Вычислим предел lim |
. Для его вычисления воспользуемся разложением |
|||||||||||||
x −1 |
||||||||||||||
|
|
x→1 |
|
|
|
|
|
|
|
|
||||
функции в ряд Тейлора в окрестности точки x=1, которое имеет следующий вид
ex = e +e |
x −1 |
|
(x −1)2 |
(x −1)3 |
|
|
|
(x −1)n |
∞ |
(x −1)n |
|
||||
|
|
+e |
|
|
|
+e |
|
+ |
... +e |
n! |
+... = e ∑ |
n! |
. |
||
1! |
|
2! |
|
3! |
|||||||||||
|
|
|
|
|
|
|
|
n=0 |
|
||||||
После подстановки такого разложения экспоненты в предел получаем |
|
||||||||||||||
lim ex −e = lim |
e |
|
1+ |
∑∞ (x −1)n |
−1 |
= e ∑∞ lim (x −1)n−1 |
= e . |
|
|||||||
|
|
||||||||||||||
x→1 x −1 |
x→1 x −1 |
|
n=1 n! |
|
|
|
n=1x→1 n! |
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13

Применение разложения функций в ряд Тейлора для вычисления интегралов
Для вычисления интегралов, не вычисляемых в элементарных функциях, также возможно использование разложения подынтегральной функции или её части в ряд Тейлора.
Пример 15
Вычислим интеграл ∫ sinx(x)d x . Для его вычисления воспользуемся разложени-
ем функции в ряд Маклорена. После подстановки рассмотренного ранее разложения синуса в интеграл получаем
|
sin (x) |
|
1 |
∞ |
(−1)n |
+ |
x2n−1 |
∞ |
(−1)n+1 |
|
∞ |
(−1)n+1 x2n−1 |
||
∫ |
|
d x =∫ |
|
∑ |
1 |
|
d x = |
∑ |
|
|
∫ x2n−2d x = |
∑ |
|
|
x |
|
|
|
(2n −1)! |
(2n −1)!(2n −1) |
|||||||||
|
|
x n=1 |
|
|
(2n −1)! |
n=1 |
|
n=1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
Пример 16
Вычислим интеграл ∫ expx(x)d x . Для его вычисления воспользуемся разложе-
нием функции в ряд Маклорена. Подстановка данного разложения в интеграл получаем
|
exp (x) |
|
1 |
∞ |
xn |
∞ |
|
∫ |
x |
d x =∫ |
|
∑ |
|
d x = ∫ ∑ |
|
|
|
||||||
|
x n=0 |
n! |
n=0 |
||||
xn−1 |
|
∞ |
xn |
|
|
d x = |
∑ |
|
. |
n! |
|
|||
|
n=0 n!n |
|
||
Применение разложения функций в ряд Тейлора для приближённых вычислений
Если необходимо вычислить функцию в заданной точке с заданной точностью, то для этого может быть использование разложения функции в ряд Тейлора. Рассмотрим это на следующем примере.
Пример 17
Вычислить значение функции sin(18°) с точностью до 10-4. Для этого воспользуемся разложением функции в ряд Маклорена. После подстановки в данное ранее разложение синуса значение угла в радианах (18°=π/10) получаем
o |
π |
|
|
|
π |
|
π3 |
|
π5 |
|
π7 |
|
|||
sin (18 |
)= sin |
|
|
|
= |
|
|
− |
|
+ |
|
− |
|
+... = |
|
10 |
10 |
3!103 |
5!105 |
7!107 |
|||||||||||
|
|
|
|
|
|
|
|
||||||||
= 0,314 −0,0052 + 2,628 10−7 −6 10−8 +...
Изданногосоотношенияследует, чтодлявычислениязначенияфункции sin(18°) с точностью до 10-4 достаточно первых двух членов разложения, т.к. остальные члены разложения по модулю меньше заданной точности. Таким образом, можно записать
sin(18°)≈0,314-0,0052=0,3088.
14
Пример 18
Вычислим значение функции cos(18°) с точностью до 10-4. Для этого воспользуемся разложением функции в ряд Маклорена. После подстановки в рассмотренное ранее разложение косинуса значение угла в радианах (18°=π/10)
o |
π |
|
|
π2 |
|
π4 |
|
π6 |
|
|||
cos (18 |
)= cos |
|
|
|
=1− |
|
+ |
|
− |
|
+... = |
|
10 |
2!102 |
4!104 |
6!106 |
|||||||||
|
|
|
|
|
|
|
||||||
=1-0,0494+4,0587 10-4-1,3353 10-6+…
Изданногосоотношенияследует, чтодлявычислениязначенияфункцииcos(18°) с точностью до 10-4 достаточно первых трёх членов разложения, т.к. остальные члены разложения по модулю меньше заданной точности. Таким образом, можно записать
cos(18°)≈1-0,04935+4,05871 10-4=0,9511.
Применение степенных рядов для решения дифференциальных уравнений Решение дифференциального уравнения F (x, y, y',..., y(n))= 0 может быть опре-
делено в виде степенного ряда |
y = |
∞ |
∑an xn . На первом этапе коэффициенты an |
||
|
|
n=0 |
будем считать неизвестными. Для их определения подставим рассмотренный ряда в исходное дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях x.
Пример 19 Рассмотрим уравнение
y'(x)+ 2 y = 4x .
Подстановка рассмотренного выше ряда в данное дифференциальное уравнение позволяет получить
∞ |
∞ |
∑n an xn−1 + 2 |
∑an xn = 4x . |
n=0 |
n=0 |
Далее приравниваем коэффициенты при одинаковых степенях x. В результате такй операции получаем
a1+a0=0; 2a2+2a2=4; 3a3+3a3=0; 4a4+2a3=0; 5a5+2a4=0; …; nan+2an-1=0; ...
Данная система уравнений может быть решена относительно произвольного коэффициента a0. Тогда
a1=-a0; an≥2=(-1)n2n+1(2+a0)/n!, |
y = a0 −a0 x + |
∞ |
(−1)n 2n+1(2 |
+ a0 ) |
x |
n |
. |
|
∑ |
|
|||||||
n! |
||||||||
|
|
n=0 |
|
|
|
|||
Пример 20
15

Рассмотрим уравнение
y'(x)+ y = cos (x).
В данном случае разложим функцию f(x)=cos(x) в ряд Маклорена. Далее подставим разложение косинуса и предполагаемую форму решения уравнения
y = |
∞ |
|
|
|
|
|
|
|
∑an xn в рассматриваемое дифференциальное уравнение, что позволяет |
||||||||
|
n=0 |
|
|
|
|
|
|
|
получить |
|
|
|
|
|
|
|
|
|
∞ |
∞ |
∞ |
(−1)n |
x |
2n |
|
|
|
∑n an xn−1 + |
∑an xn = |
∑ |
|
|
. |
||
|
2n! |
|||||||
|
n=0 |
n=0 |
n=0 |
|
|
|||
Далее приравниваем коэффициенты при одинаковых степенях x. В результате такой операции получаем
a1+a0=1; 2a2+a1=0; 3a3+a2=-1/2; 4a4+a3=0; 5a5+a4=1/24;
…; (n +1)an+1 + an = |
(−1)sin (π n 4) |
1 −(−1)n+1 |
|
; ... |
|
2 |
(11n − 20)! |
||||
|
|
||||
Полученная система уравнений может быть решена относительно произвольного коэффициента a0. Тогда
1 |
|
(−1)sin (π n 4) |
1−(−1)n+1 |
|
||
an+1 = |
|
|
2 |
|
|
−an . |
n +1 |
(11n −20)! |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Ряд Фурье
Тригонометрическим рядом Фурье называется ряд следующего вида
a |
0 |
∞ |
|
|
π n x |
∞ |
|
|
π n x |
|
+ ∑a |
|
cos 2 |
|
+ ∑b |
sin 2 |
, |
||
2 |
|
||||||||
n=1 |
n |
|
L |
n=1 |
n |
|
L |
||
где n – целое число, находящееся в пределах суммирования (в нашем случае n [1,∞]), x [a,b], L=b-a. рассмотренный ряд может иметь следующие эквивалентные формы
|
∞ |
|
π n x |
+ϕ |
|
, B |
∞ |
|
π n x |
+ψ |
|
||
A + ∑ A |
cos |
L |
|
+ ∑B |
sin |
L |
. |
||||||
0 |
n=1 |
n |
|
|
n |
0 |
n=1 |
n |
|
|
n |
||
При приближенной замене функции f(x) тригонометрической суммой
sn (x)= |
a |
0 |
N |
|
|
π |
|
+ ∑ an cos |
2 |
|
|||
2 |
|
|||||
|
n=1 |
|
|
|
||
среднеквадратическая ошибка
n x |
N |
|
|
π n x |
|
+ ∑ b |
sin 2 |
|
|
L |
n=1 |
n |
|
L |
16

U = 1 T∫[f (x)− sn (x)]2 d x
T 0
будет наименьшей, если коэффициенты an и bn выбрать следующим образом
|
2 |
L |
|
π n x |
2 |
L |
|
π n x |
an = |
|
∫ |
f (x)cos 2 |
d x , bn = |
|
∫ |
f (x)sin 2 |
d x , |
|
|
|||||||
|
L 0 |
|
L |
L 0 |
|
L |
||
где L – в данном случае является периодом тригонометрической функции. Замечание 3
Функция f (x) может быть разложена в ряд Фурье по функциям fn(x), отличным от тригонометрических, если они удовлетворяет следующим условиям
1) T∫ fn (x) fm (x) d x = 0 при m≠n и T∫ fn2 (x) d x ≠ 0 ;
0 |
0 |
2)функции fn(x) позволяют учесть и симметричную компоненту функции f (x),
ине симметричную компоненту функции f (x), и постоянную составляющую
|
|
|
2 L 2 |
|
|
|
π n x |
|
|
2 |
|
L |
|
|
|
|
|
|
π n x |
|
|
1 |
|
|
||||||
an = |
|
|
|
∫ cos |
2 |
|
d x + |
|
|
∫ |
(−1)cos |
2 |
|
d x = |
|
|
|
sin (π n)− |
||||||||||||
|
L |
L |
|
|
L |
π n |
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
L L 2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
− |
|
1 |
|
[sin (2π n)−sin (π n)] |
= |
2 |
sin |
(π n)− sin (2π n) |
|
= 0 . |
|||||||||||||||||
|
|
|
π n |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π n |
|
|
|
|
π n |
|
|
|
|
||||||
Вычисление коэффициентов bn позволяет получить |
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
L 2 |
|
|
|
π n x |
|
2 |
|
L |
|
|
|
|
|
π n x |
|
1 |
|
[1 |
−cos (π n)]− |
|||||||||
bn = |
|
|
∫ sin |
2 |
|
|
d x + |
|
|
∫ |
(−1)sin |
2 |
|
|
d x = |
|
|
|||||||||||||
L |
|
|
|
|
|
|
|
π n |
||||||||||||||||||||||
|
0 |
|
|
|
|
|
L |
|
L L 2 |
|
|
|
|
|
|
L |
|
|
|
|
||||||||||
−π1n [cos (π n)−cos (2π n)]= (−1)n π2n .
Вокончательной форме ряд Фурье имеет следующий вид
f (x)= |
4 |
∑∞ sin [2 (2n +1)x]. |
|
|
|||
|
π n=0 |
2n +1 |
|
17
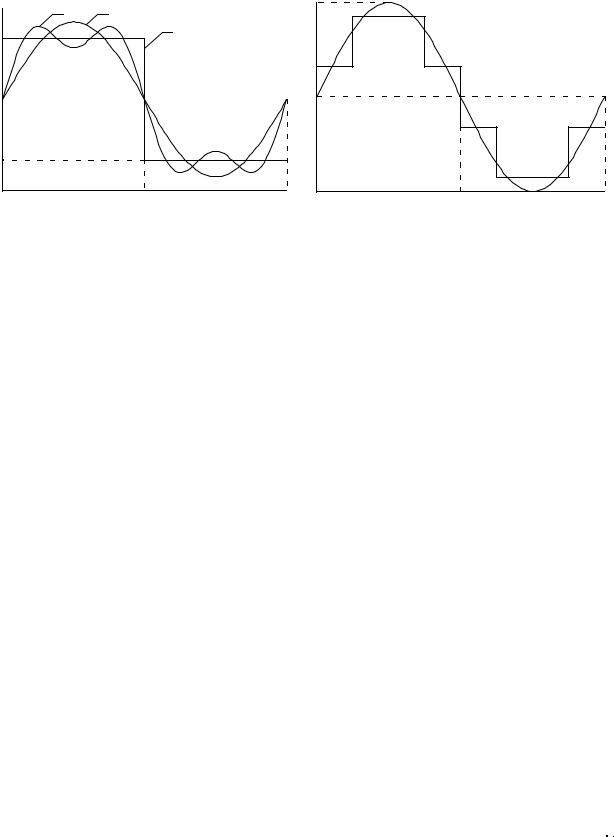
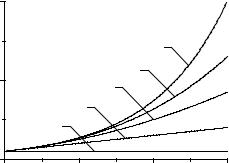
Рассматриваемая функция, её первый член разложения в ряд Фурье и сумма её первых двух членов разложения в ряд Фурье представлены на рис. 3 (соответственно кривые 1, 2 и 3). Пример обратного разложения представлен на рис. 4.
f (x) |
2 |
|
1 |
3 |
|
||
|
|
||
1 |
1 |
|
|
|
|
|
|
0 |
|
|
0 |
-1 |
|
|
|
0 |
L/2 |
L |
x-1 |
0 |
|||
|
Рис. 3. |
|
|
L/2 |
L |
Рис. 4.
Пример 22
Разложим функцию следующего вида: f (x)= 0, −π ≤ x ≤ 0 в ряд Фурье на ин-
x, 0 ≤ x ≤π
тервале x [-π,π] Вычисление коэффициентов an приводит к следующему результату
|
|
|
|
a = |
1 |
0∫ f (x)d x + |
1 |
π∫ f (x)d x |
= 0 + |
x2 |
|
= π , |
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
0 |
2π −π |
|
|
|
|
2π 0 |
2 |
|
4 |
|
|
|
|||||||
an≥1 = |
1 |
0∫ f (x)cos (n x)d x + |
1 |
π∫ |
f (x)cos (n x)d x = 0 + |
1 π∫sin (n x)d x = |
||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
π −π |
|
|
|
|
|
|
π 0 |
|
|
|
|
|
|
n 0 |
|
||||
|
|
|
|
|
= |
1 |
|
[cos (π n)−1]= (−1)n −1 . |
|
|
|
|
||||||||||
|
|
|
|
|
n2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|||||
Вычисление коэффициентов bn позволяет получить |
|
|
|
|
||||||||||||||||||
0 |
|
|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
|
|
π |
= [1−(−1)n ]πn . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
bn≥0 = |
1 |
−∫π f (x)sin (n x)d x + |
|
0∫ f |
(x)sin (n x)d x = − πn cos (π n) |
|
−π |
|||||||||||||||
π |
π |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
В окончательной форме ряд Фурье имеет следующий вид |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
∞ |
|
n |
|
|
|
∞ |
[1−(−1)n ]sin (n x). |
||||||||||
|
|
|
f (x)= π + ∑1−(−1) |
cos |
(n x)+ ∑ |
1 |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
4 |
n=1 π n2 |
|
|
|
n=1π n |
|
|
|
|
|
|
|
|||||||
5.Применение рядов в экономике
Внастоящем разделе мы рассмотрим две задачи, касающиеся последовательно-
стей и рядов, применительно к экономическим задачам. Пусть имеется вклад 



 (рублей) в банке. По прошествии определенного промежутка времени банк на-
(рублей) в банке. По прошествии определенного промежутка времени банк на-
18
