Конспект до лекції 2

Тема 2. Аналітичне розв’язання задач орієнтування моделі

Тематичний план

2.1.Задача аналітичного взаємного орієнтування пари знімків.

2.2.Сумісне визначення елементів взаємного орієнтування та передача масштабу для двох суміжних моделей.

2.3.Задача абсолютного орієнтування моделі

2.1. Задача аналітичного взаємного орієнтування пари знімків.

2.1.1. Строгий спосіб

Задача полягає у знаходженні елементів взаємного орієнтування у вибраній системі - лінійно-кутовій чи базисній. Для обох систем порядок розв’язання задачі однаковий, а різниця полягає лише в тому, що в лінійно-кутовій системі використовується рівняння (1.13), а в базисній рівняння (1.17).

Ці рівняння отримані нами раніше. Подамо розв’язок для обох систем.

Для базисної системи необхідно знайти елементи взаємного орієнтування л , п , л , п , п . Рівняння взаємного орієнтування

отримують диференціюванням (2.1) з врахуванням залежностей визначення координат точок

косинусів. Подамо ці формули в кінцевому вигляді:

Вільний член l обчислюється за формулою (2.6).

Тут індекс 1 стосується лівого знімка, індекс 2 – правого знімка. Напрямні косинуси а1, а2, b1,

взаємного орієнтування, а значить, вимірявши його в декількох точках стереопари, можемо знайти елементи взаємного орієнтування. Так як кожен вимір точки моделі дає одне рівняння точки, а невідомих маємо п’ять, то значить, що на стереопарі необхідно провести виміри щонайменше в п’яти точках. При використанні аналітичного способу число точок n , як правило, значно більше, і це дозволяє точніше визначити елементи взаємного орієнтування. При n>5 застосовують метод найменших квадратів (МНК).

Послідовність розв’язання задачі (для обох систем взаємного орієнтування) така:

1. Задаються наближеними значеннями елементів взаємного орієнтування

2.Для кожної виміряної точки стереомоделі (тобто для ідентичних точок на лівому і правому знімках) обчислюють коефіцієнти та вільний член рівнянь поправок за

формулами (2.6) або (2.9) і умови r = k R .

В результаті цих дій формується матриця коефіцієнтів

3. З усіх рівнянь поправок (2.5) чи (2.8), враховуючи матричний запис (2.10) і (2.11) отримуємо систему рівнянь поправок

де X - матрицястовпчик шуканих поправок до наближених значень елементів взаємного орієнтування

Для елементів в лінійно-кутовій системі обчислення аналогічні.

5. Оскільки ми використовували прийом ліанеризації нелінійних функцій, то для досягнення точного результату застосовуємо метод послідовних наближень (ітераційний процес).

Тому перевіряємо ітераційний процес на збіжність:

При виконанні всіх умов (2.18) ітераційний процес завершено і переходять до пункту 6. Якщо хоча б одна з умов (2.18) не задовільняється, то повертаємось до пункту 2.

6. Після завершення ітераційного процесу проводять оцінку точності класичним для МНК способом. Спочатку обчислюють середню квадратичну помилку одиниці ваги

де поправка vi обчислюється з рівняння (2.8) або (2.5), підставляючи замість невідомих їх розв’язок з останньої ітерації. Геометричний зміст величини vi - це залишковий поперечний

паралакс після знаходження елементів взаємного орієнтування.

2.1.2.Наближений спосіб

Придатний для опрацювання пари планових аерознімків (кути нахилу не перевищують

3o ).

В цьому випадку в порівнянні зі строгим способом проводять певні спрощення, які базуються на тому, що при малих кутах sin , cos 1, sin sin 2 = 0 (величина мала другого порядку в порівнянні з ). Тому рівняння (2.5) - базисна система - матиме вигляд:

паралакс. Щоб спростити розв’язок, точки для вимірювання вибирають не довільно, а в т.зв. стандартних зонах стереопари (рис.1.3).

Рис.2.1 Стандартні зони для визначення елементів взаємного орієнтування.

Кількість точок для вимірів рівна шести, тобто маємо один надлишковий вимір, що дозволяє виконати контроль розв’язання задачі (заради об’єктивності зазначимо, що цей контроль досить слабкий). З рис.2.1 можемо записати координати точок:

координат шести точок рівняння (2.21) можна розв’язати аналітично і отримати наступні формули для безпосереднього обчислення елементів взаємного орієнтування в базисній системі:

Для елементів взаємного орієнтування в лінійно-кутовій системі з рівнянь (2.22) отримаємо аналітичний розв’язок:

Точність визначення елементів взаємного орієнтування можна підрахувати з формул (2.26),

які отримують шляхом диференціювання виразів (2.24) або (2.25), вважаючи, що поперечні паралакси виміряні із середньою квадратичною помилкою mq :

Аналіз цих формул показує, що точність визначення елементів взаємного орієнтування залежить від величини фокусної віддалі знімків - для короткофокусних аерокамер точність є кращою, аніж для довгофокусних. Чим більше перекриття між знімками, тим менший базис, і точність є гіршою.

Окрім цих геометричних параметрів на точність розв’язання задачі істотно впливає похибка виміру поперечного паралаксу. Якщо кілька десятиліть тому на виробництві опрацьовували знімки, для яких mq 0.02мм , то зараз маємо значно кращі за геометричними

та спектральними характеристиками знімки, так що mq 0.002 − 0.005мм . Це означає, що

точність визначення елементів взаємного орієнтування зросла на порядок.

Дослідження показали, що точність визначення кутів л,п , п є кращою, аніж для кутів κл, п; для лінійно-кутової системи елементи , , визначаються краще, ніж кути , .

Задача взаємного орієнтування розв’язується погано або зовсім не розв’язується, якщо сфотографована поверхня близька до поверхні циліндра, твірна якого паралельна до базису фотографування. Це так звана “умова невизначеності взаємного орієнтування”. Тоді детермінант матриці нормальних рівнянь є або нулем, або близький до нуля.

Професор І. Антіпов довів, що цього негативного явища можна позбутись, якщо до рівнянь взаємного орієнтування додається умова рівності координат зв’язкових точок.

2.2. Сумісне визначення елементів взаємного орієнтування та передавання масштабу для двох суміжних моделей

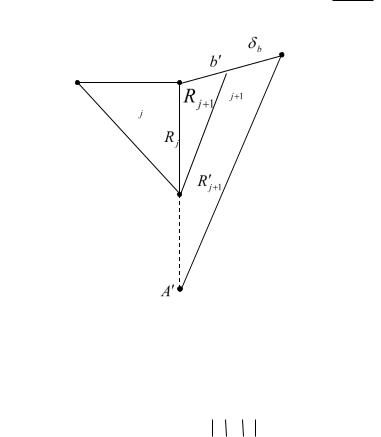
Нехай визначені елементи взаємного орієнтування j-ї моделі за формулою (2.11) та розв’язана пряма фотограмметрична засічка, тобто в j-й моделі визначено координати точки А (початок координат у точці S2). Необхідно одночасно знайти елементи взаємного орієнтування (j+1)-ї моделі та виконати приведення масштабу (j+1)-ї моделі до масштабу попередньої j-ї моделі (рис. 2.2). Як відомо, визначення елементів взаємного орієнтування виконується на підставі виміряних поперечних паралаксів, а передавання масштабу виконується за зв’язковими точками. Математичне формулювання задачі полягає у використанні рівняння (2.12) взаємного орієнтування та рівності векторів

A

Рис. 2.2. З’єднання двох моделей за зв’язковими точками

Строго кажучи, рівняння (2.28) є нелінійним відносно шуканих елементів, , , , , b і тому треба було б застосувати описаний вище прийом лінеаризації

Отже, для всіх точок (j+1)-ї стереопари складається система рівнянь (2.12), до неї долучаються рівняння (2.30), записані для зв’язкових точок, і одночасно розв’язується система нормальних рівнянь з 6 невідомими

Уразі застосування МНК послідовність розв’язання така:

1.Для кожної зв’язкової точки розв’язують пряму фотограмметричну засічку у j-й моделі.

2.Задаються наближеними значеннями елементів взаємного орієнтування та базису в (j+1)-

3.Для кожної пари виміряних точок обчислюють коефіцієнти та вільні члени (2.6).

4.Для кожної зв’язкової точки розв’язують пряму фотограмметричну засічку у (j+1)-й моделі, використовуючи спочатку наближені (а потім уточнені) параметри (елементи взаємного орієнтування та базис).

5.Для кожної зв’язкової точки складають рівняння (2.30).

6.Складають нормальні рівняння, отримують розв’язок (2.31).

7.Обчислюють уточнені значення невідомих

9. Оцінка точності розв’язання задачі аналогічна до (2.11), тільки в знаменнику стоятиме величина (n–6).

Зазначимо, що геометричну сутність рівнянь (2.28) вперше використав проф. А. Скірідов, назвавши їх “умовою бокових сторін”. Він також запропонував використати цю умову для уточнення кутового орієнтування моделі на універсальних стереоприладах.

Як вже зазначалось, проф. І. Антіпов застосував цю саму умову у побудові мережі маршрутної фототріангуляції методом залежних моделей. Таке одночасне розв’язання задачі визначення елементів взаємного орієнтування та передавання масштабу принципово змінило проблему “невизначеності елементів взаємного орієнтування”. Оскільки детермінант сукупної системи нормальних рівнянь відрізняється від нуля, то розв’язок задачі є завжди стабільним.

2.3. Задача абсолютного орієнтування моделі

У результаті розв’язання прямої фотограмметричної засічки, описаного в п. 4.1, отримують просторові координати точки А моделі об’єкта . Якщо система SXYZ є абсолютною (геодезичною), і кути нахилу знімків та базису визначені в цій системі, то зрозуміло, що модель будується в абсолютній системі координат.

Проте найчастіше система SXYZ є відносною, і тому треба знайти елементи геодезичного орієнтування моделі:

З геометричного погляду ця задача складається з трьох дій:

–перенесення початку координат з центра OФ у центр O;

–“поворот простору”;

–зміна масштабу моделі, тобто приведення його до величини t.

Формули перетворення координат є такими: