Добавил:

Justeeeek100500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

Фотограмметрия

Файл:

Конспект до лекції 1

.pdf

Скачиваний:

Добавлен:

28.06.2022

Размер:

476.63 Кб

Скачать

☆

Тема 1. Математичні основи аналітичної фотограмметрії

Тематичний план

1.1.Умова та рівняння колінеарності векторів.

1.2.Умова та рівняння компланарності векторів.

1.3.Геометричні перетворення.

1.1. Умова та рівняння колінеарності векторів.

При розгляді фізичних та геометричних основ фотограмметрії ми постійно оперуємо з поняттям вектора.

Вектор - це величина, що має довжину і напрямок. Вектори, що лежать на одній прямій або паралельні між собою, називають колінеарними.

B фотограмметрії бачимо, що промінь, який виходить з центра проекції S до точки об'єкта А записує образ цієї точки на знімку, тобто маємо вектор r (рис. 1.1)

Оскільки ці вектори пропорційні, то можемо записати r = k R . Перейдемо від векторів до координат точок а та А.

Рис.1.1. Колінеарність двох векторів

Якщо системи координат знімка і об’єкта мають спільний початок в точці S, а осі обох систем паралельні, то на підставі рис.1.2 можемо отримати:

	f		y =	f
x =		X			Y	(1.1)

	Z			Z

Якщо прийняти, що координата Z дорівнює висоті аерознімання H, то з рис.1.2 отримаємо формулу для обчислення масштабу знімка в ідеальному випадку

1:m= f:H

(1.2)

Ця проста формула відіграє особливу роль в фотограмметрії.

Якщо початок координат системи знімка не співпадає з головною точкою, необхідно виконати паралельне перенесення системи координат в точку о

Тоді

x = x − x0

y = y − y	0

(1.3)

− =

−

Рис.1.2. Пропорційність векторів та координат.

Якщо ж початок просторової системи координат не співпадає з точкою S, а осі обох систем не паралельні, то необхідно виконати такі операції.

Спочатку треба перенести початок системи з точки О в точку S; а потім виконати поворот просторової системи на кути Ейлера ( , , ).Тому маємо

X − X		S	X

	Y − YS			(1.4)
			= A , , Y
			Z
Z − Z		S

де A , ,

- матриця напрямних косинусів . З математики відомо, що матриця

A , ,

матрицею ортогональною, тому транспонована та обернена матриці рівні, тобто

= A

−1

(1.5)

, ,

Тому з (1.4) маємо,

X − X

Y − YS

(1.6)

Z − Z

X = a1 (X − X S ) + b1 (Y −YS ) + c1 (Z − ZS ) ,

Y = a2 (X − X S ) + b2 (Y −YS ) + c2 (Z − Z S ) ,

(1.7)

Z = a3 (X − X S ) + b3 (Y −YS ) + c3 (Z − ZS ) .

Підставивши рівняння (1.3) та ( 1.7) в (1.1) остаточно отримаємо:

x − xo = − f

( X − X S ) + b1 (Y − YS ) + c1 (Z − Z S )

( X − X S ) + b3 (Y − YS ) + c3 (Z − Z S )

(1.8)

( X − X

) + b

(Y − Y

) + c

(Z − Z

)

y − yo = − f

( X − X

) + b

(Y − Y

) + c

(Z − Z

)

Ці рівняння часто називають рівняннями колінеарності.

1.2. Умова та рівняння компланарності векторів

З математики відомо: якщо три вектори лежать в одній площині, то їх називають компланарними. Звернемось до рис.1.3.

На ньому показано три вектори, які в фотограмметрії можна трактувати так: вектор b - базис фотографування, R1 i R2- проектуючі промені, що виходять з лівого S1та правого S2 центрів фотографування до точки A об’єкта.

	2

1	2

Рис.1.3. Умова компланарності 3-х векторів (, 1, 2).

Скористаємось відомостями з математики: якщо три вектори b, R1, R2 компланарні (тобто лежать в одній площині), то для них справедливе рівняння

b (R	R ) = 0
1	2

(1.9)

Це змішаний склярно-векторний добуток.

Спроектуємо кожний з векторів на осі координат Х,Y,Z і запишемо:

b =

Тоді рівняння (1.9) матиме вигляд:

= 0

(1.11)

Розкладання детермінанта (1.11) по першому рядку дає:

(1.10)

b	Y	Z		− b		X
b	1		1	− b
	1		1
x	Y	Z			y	X
	Y	Z	2			X
	2		2

	Z		+ b	X
1		1

	Z		z	X
2		2

	Z		= 0
1		1

2	Z	2

(1.12)

Подальші математичні дії залежать від того, яку просторову систему координат (систему взаємного орієнтування) ми виберемо.

Для лінійно-кутової системи базис проектування має всі три компоненти bx, by, bz. Оскільки bх ніколи не рівне нулю, то з (1.12) отримаємо:

Y	Z		−	b	y	X		Z		+	b	X		Z		= 0
1	1		−				1		1	+	z		1		1	= 0
1	1						1		1		z		1		1
Y	Z	2		b		X	2	Z	2		b	X	2	Z	2
2		2			x		2		2		x		2		2

Так як маємо

(1.13)

by	= tg ,	b	z	=	tg	, (1.14)

bx		bx			cos

то з (1.13) отримаємо рівняння взаємного орієнтування для лінійно-кутової

системи:

F = (Y Z		−Y Z ) − tg ( X			Z		− X		Z ) +	tg	( X	Z		− X		Z ) = 0	(1.15)
	2					2		2					2		2
1		2	1	1					1	cos	1					1

Для базисної системи взаємного орієнтування bz=0. Тому з (1.12) отримаємо:

b (Y Z	2	−Y Z ) =
x 1	2	2 1

bx ніколи не рівне нулю, натомість by=0

(1.16)

або кінцеве рівняння взаємного орієнтування для базисної системи

F = Y Z	2	−Y Z = 0
1		2	1

(1.17)

Рівняння (2.19) та (1.11) є базовими для знаходження елементів взаємного орієнтування

1.3.Геометричні перетворення.

Вфотограмметрії приходиться оперувати такою математичною категорією як перетворення простору. Найбільш уживаним є проективне перетворення двоабо тримірного простору. Подамо в стислій формі найбільш поширені в фотограмметрії типи перетворень.

1.Проективне; має вигляд:

y		T	y ,	(1.18)
		= A

де А - матриця перетворень, ( det A 0 ), y - вектор початковий,

- вектор перетворений.

2. Афінне; має вигляд:

x		= Ax + b , (1.19)

де А - матриця перетворення, x, x´, b - вектори-стовпчики.

Властивості цього перетворення: площина, лінія і відрізок переходять відповідно у площину, лінію і відрізок; не порушується паралельність прямих і площин; зберігається метрика векторів; трикутник переходить в трикутник.

Особливий випадок цього типу перетворення:

x =

при умові, що

RAx + b

(1.20)

A	−1	T
A		= A

тобто А - ортогональна матриця, а вектор

R є діагональною матрицею, тобто

(1.21)

	R
		11
			R
R =			R	22		.
				22



					Rmm

3.Афінне при співпадінні осей координат; має вигляд:

x = Ax ,

тут det A 0 .

4.Афінне зі збереженням подібності; має вигляд:

(1.22)

(1.23)

x		= kAx + b ,

де k>0,	A	−1	T
			= A .

Властивості цього перетворення:

-кути зберігаються;

-зберігається подібність фігур;

-зберігається пропорційність відрізків;

-не порушується перпендикулярність векторів.

5.Афінне подібне середнє:

(1.24)

тобто отримане з (1.22) за умови координат.

6.Гомотетія:

тобто з (1.25) k=1.

7.Ізометрія:

	,
= kAx	,
b=0. В

(1.25)

цьому випадку зберігається початок системи

= Ax ,

(1.26)

x = Ax +b .

(1.27)

Тут зберігаються довжини векторів.

8.Ізометрія середня:

x = Ax .

(1.28)

Тут збігаються початки систем координат.

9.Поворот простору:

x = Ax ,

де	A	−1	T	, det A =1.
			= A

10.Перенос:

	= x +b ,
x	= x +b ,
A = E , k =1.

Властивість: міняється початок системи координат.

11.Симетричне відображення:

	x	= −x ,
	x	= −x ,
A = E , k =1	, витікає з (1.25).

Властивість: міняється орієнтування в просторі. 12. Ідентичне перетворення:

(1.29)

(1.30)

(1.31)

x =

(1.32)

тут зберігаються всі елементи.

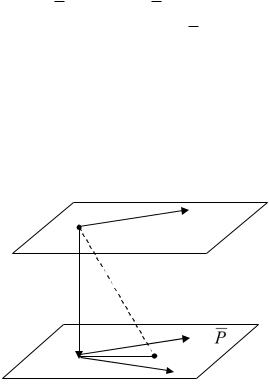
Звернемо тепер увагу на деякі аспекти геометричних перетворень. Спочатку

розглянемо перетворення площини E в площину P (рис.1.4).


Для визначення положення точки а на площині			P	прийнята довільна (не прямокутна)
система координат		. Для так званих невласних		точок (перетин двох паралельних
	O x1 x2

прямих) ці координати не дозволяють визначити їх положення. Тому в проективній геометрії положення точки визначається його напрямком. Напрямок вектора визначається співвідношенням його складових k : m . Тому для будь-якої точки а (рис.5) визначальним є відношення:

y	: y	: y
1	2	3

x	: x
1	2

(1.33)

O ~ Рис.1.4 x1 a(x1, x2)


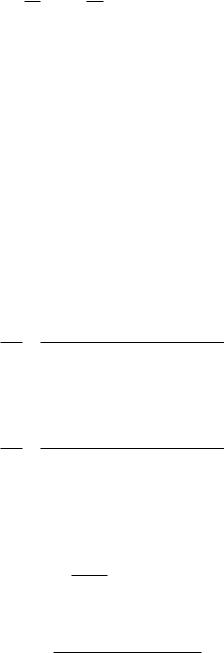
Координати y1 , y2 , y3 називають однорідними координатами точки а в системі O x1 x2
. Співвідношення (1.33) означає пропорційність складових k.
Для кожної точки площини можна записати
k y : k y	: k y	= x1 : x2 :1.	(1.34)
1	2	3
Звідси можна зробити висновок, що системі однорідних координат у			(n+1) - мірному

просторі може відповідати довільна система координат n - вимірного простору. З (1.33) маємо:

x	=
1

y1 y3

x	2	=
	2

y	2

y
	3

(1.35)

Для тривимірного простору необхідно взяти чотири числа, тобто (1.33) запишеться так:

y1 : y2 : y3 : y4			= x1 : x2 : x3 :1,				(1.36)
k y	: k y	2	: k y	: k y	= x1 : x2	: x3	:1 .
1		2		3	4

Якщо прийняти до уваги (1.18) - лінійне перетворення, то для четвірки чисел запишемо:

k y			= a11 x1 + a12 x2	+ a13 x3	+ a14 x4 ,
	1
k y		2	= a21 x1 + a22 x2	+ a23 x3	+ a24 x4 ,	(1.37)
		2
k y	3		= a31 x1 + a32 x2	+ a33 x3	+ a34 x4 ,
k y	4		= a41 x1 + a42 x2	+ a43 x3	+ a44 x4 .
	4

З (1.37) та (1.36) легко отримуємо формули для обчислення координат при геометричних проективних перетвореннях.

Для тривимірного простору:

		k y			=	a		x		+ a				x		+ a				x		+ a					x			,
				1	=		11	1					12		2			13			3			14				4		,
				1			11	1					12		2			13			3			14				4
		k	y			a	41	x		+ a			42	x	2	+ a			43	x	3	+ a			44		x		4
			y	4			41	1					42		2				43		3				44				4
k y	2			a	x + a				22		x	2	+ a			23	x	3	+ a			24	x	4
	2	=			21 1				22			2				23		3				24		4		,
k y4		=		a41 x1 + a42 x2 + a43 x3 + a44 x4																						,
k y4				a41 x1 + a42 x2 + a43 x3 + a44 x4
		k y			=	a		x		+ a				x		+ a				x		+ a					x			.
				3	=		31	1					32		2				33		3				34				4	.
				3			31	1					32		2				33		3				34				4
		k	y			a	41	x		+ a			42	x	2	+ a			43	x	3	+ a			44		x		4
			y	4			41	1					42		2				43		3				44				4

Ставиться вимога, що det A 0 .

Рівняння (1.38) можна спростити, розділивши чисельник і знаменник в (1.38) на Ввівши позначення для величин

a x

11 1

= A x ,

= A

y ,

= A z

і т.д.,

a44 x4

a44

a44 x4

отримаємо:

(1.38)

a44 x4 .

(1.39)

x + A

y + A

z + A

x + A

y + A z +1

A21 x + A22 y + A23 z + A24

(1.40)

A41 x + A42 y

+ A43 z +1

A31 x + A32 y + A33 z + A34

A41 x + A42 y + A43 z +1

Для двомірного простору (перетворення площини в площину) маємо відповідно:

y	3	= 0,	z = 0
	3

						A	x + A		y + A
			y1		=	11		12		13	,
			y1		=	A		x + A		y +1	,
						A		x + A		y +1
						41		42
		A		x + A			y + A
y2	=	21				22		23	.
y2	=	A			x + A			y +1	.
		A			x + A			y +1
			41			42

Для одномірного простору (перетворення прямої в пряму) відповідно запишемо:

y1 = A11 x ++A12 .

A21 x 1

(1.41)

(1.42)

Дуже важливим є перетворення “Поворот простору”, яке описується рівнянням (1.29) за умови ортогональності матриці А. Тоді тримірний евклідовий простір перетворюється в такий самий. Це означає, що y4 та x4 відсутні. Тоді (1.29) запишеться так:

y1 = a11x1 + a12 x2 + a13 x3 ,

y	2	= a	21	x
	2		21	1

			y
			3
Матриця
	a
		11
A =		a
A =		a	21
			21
	a		31
			31

+ a22 x2 + a23 x3						,
= a		x + a			x	+ a	x
	31	1		32	2	33	3
a		a
12			13
a		a
a	22	a	23
	22		23
a	32	a	33
	32		33

(1.43)

(1.44)

називається матрицею напрямних косинусів і описує поворот однієї системи координат відносно іншої. В аналітичній геометрії положення (повороти) однієї системи координат

відносно іншої описуються кутами Ейлера

. Перетворення (1.43) відбувається за

допомогою матриці А, а взаємне положення осей координат визначають коефіцієнти, подані в таблиці:

осі	x1	x2	x3

y1	a11	a12	a13
y2	a21	a22	a22
y3	a31	a32	a33

В залежності від порядку поворотів осей координат для напрямних косинусів

отримати відповідні формули. Найбільш поширеним є порядок поворотів

→ →

Опускаючи викладки, запишемо елементи матриці напрямних косинусів:

можна

a	= cos cos −sin sin sin
11

a12

= −cos sin

−sin sin cos

a13 = −sin cos ,

a	21	= cos sin
	21

a22 = cos cos ,		(1.45)
a23	= −sin ,
a31	= sin cos + cos sin sin ,
a32	= −sin sin + cos sin cos ,
a33	= cos cos .

Для елементів матриці А справедливі рівняння:

	2		2		2				a11a21 + a12a22 + a13a23	= 0
	a11	+ a12		+ a13		= 1		,	a11a21 + a12a22 + a13a23	= 0	,
2		2		2					a21a31 + a22a32 + a23a33 = 0
a21	+ a22		+ a23		= 1		,		a21a31 + a22a32 + a23a33 = 0	,
	2		2		2		= 1,		a31a11 + a32a12 + a33a13 = 0 .
	a31	+ a32		+ a33			= 1,		a31a11 + a32a12 + a33a13 = 0 .

Якщо відомі напрямні косинуси, то можна знайти кути , , :

(1.46)

		a
	−	13		,
= arctg	−			,

		a33
= arcsin(−a23 ) ,				(1.47)
a		21
		21	.
= arctg			.

a22

Примітка. В наступних розділах матриця (1.77) записується так:

	a		a	2	a	3
		1		2		3
A =		b1	b2		b3		.
A =		b1	b2		b3		.

	c		c	2	c	3
		1		2		3

(1.48)

Соседние файлы в предмете Фотограмметрия

#
28.06.20222.71 Mб3Variant-57.pdf
#
28.06.20222.71 Mб2Variant-58.pdf
#
28.06.20222.71 Mб2Variant-59.pdf
#
28.06.20222.71 Mб2Variant-60.pdf
#
28.06.2022372.65 Кб9Геометричні перетворення зображень.pdf
#
28.06.2022476.63 Кб10Конспект до лекції 1.pdf
#
28.06.20221.53 Mб8Конспект до лекції 12.pdf
#
28.06.2022450.76 Кб9Конспект до лекції 2.pdf
#
28.06.2022612.95 Кб7Конспект до лекції 3.pdf
#
28.06.2022267.15 Кб10Конспект до лекції 4.pdf
#
28.06.2022410.94 Кб9Конспект до лекції 5.pdf