Конспект лекцій 2 (Перетворення цифрових зображень)

Тема 2. ПЕРЕТВОРЕННЯ ЦИФРОВИХ ЗОБРАЖЕНЬ

Фотометрична корекція

Геометричні перетворення

В ході фотограмметричного опрацювання зображень виникає необхідність різного роду їх перетворень, пов’язаних як з покращенням читабельності, так і зміною розмірів і перебудові зображення (наприклад, при масштабуванні зображень в процесі їхнього трансформування, усуненні геометричних спотворень). В першому випадку говорять про фотометричну корекцію (оптичних перетвореннях) цифрового зображення, а в другому – про зміну його геометричного розрізнення та положення окремих елементів зображення, або про геометричні перетворення.

Спотворюючі фактори можна розділити на чотири категорії:

Глобальні фактори - рівномірно спотворюючи рівень інтенсивності характеристик всіх елементів сцени (поля) і спричинюючі геометричні спотворення різного характеру.

Регіональні фактори - рівномірно спотворюючі рівень інтенсивності характеристик тільки всередині однорідних областей сцени, наприклад, зміну контрасту або яскравості.

Місцеві фактори - незалежно діючі на кожну елементарну складову сцени або їх групу, наприклад, адитивний або мультиплікативний шуми.

Неструктурні фактори - змінюють характерні ознаки сцени, наприклад, часткове закриття сцени хмарою, спотворення сцени тінями і поту скнінням тощо.

Фотометрична корекція зображення, або оптичні його перетворення, засновані на використанні зв’язку між його компонентами, який описується рівнянням:

ρi = a∙ρi,вх.+ b, (1)

де ρi,вх., ρi – оптичні щільності елемента зображення до і після фотометричної корекції; a – функція, визначаюча відношення між оптичними щільностями вхідного і перетвореного зображень; b – параметр яскравості.

Перетворення, описане рівнянням (1), можна представити графіком (рис. 1), який відображує зв'язок оптичних щільностей елементів зображення до їхньої корекції (вертикальна вісь) і після корекції (горизонтальна вісь).

Рис.1.Графік фотометричної корекції

1

Фотометрична корекція виконується шляхом зміни яскравості зображення, його контрастності, або зміною характеру співвідношень між оптичними щільностями до і після їхнього перетворення.

Зміна яскравості виконується шляхом зменшення або збільшення параметра b кожного пікселя на одну й ту ж величину. Це приводить до стану, коли всі елементи зображення стають більш світлими або більш темними. Зміна яскравості групує щільності до якогось одного (світлого або темного) краю спектра. На графіку (рис.1) це ілюструється зміщенням прямої 1 (або кривої 2) вздовж горизонтальної осі.

Зміна контрастності зображення виконується з метою посилення чи ослаблення відмінності між щільностями суміжних (сусідніх) елементів і покращення таким чином відчуття границі між ними. Збільшення контрастності зображення виконується таким чином. Якщо оптична щільність ρвх деякого елемента перевищує середнє значення, то вона збільшується пропорційно рівню квантування, а якщо вона менша від середнього, то зменшується. При цьому значення щільностей пікселів ніби зміщуються до країв спектра: темні тони стають іще темнішими, світлі – іще світлішими. Деякі їх значення зчезають, але границі між елементами зображення стають більш чіткими. При зменшенні контрастності більші щільності зменшуються, а малі – збільшуються; при цьому щільності групуються біля центру. Надмірне збільшення контрастності перетворить напівтонове зображення до бінарного, а надмірне зменшення − веде до його зчезання. На графіку (рис. 1) такі перетворення відповідають обертанню прямої 1 (кривої 2) довкола центральної точки.

Гама-корекція (тональна корекція) зображення виконується з метою збільшення або зменшення його детальності, що досягається зміною передавальної функції a рівняння (1), що визначає характер перетворення. На графіку (рис. 1) гама-корекція відповідає зміні кривизни і загального нахилу лінії 1 (або 2).

При рівномірній передачі оптичної щільності (пряма 1 під кутом 45° до координатних осей) їхні значення, відповідні точкам A і A′, одинакові. Змінимо передавальну функцію a рівняння (1) так, щоб їй відповідало рівняння кривої 2. Тепер щільності вхідного зображення (точка A) буде відповідати щільність відкоректованого зображення A″, причому, A ≠ A″.

Слід зауважити, що неправильне застосування гама-корекції може призвести до зменшення кількості напівтонів і до переважання областей одного тону.

При опрацюванні кольорових зображень можна виконати не тільки зміну яскравості, контрастності або гама-корекцію, але й змінюючи співвідношення кольорів, отримати потрібні відтінки.

Геометричні перетворення растрового зображення змінюють його площину і частково коригують його радіометричні характеристики.

Необхідність таких перетворень виникає, наприклад, при трансформуванні цифрового знімка за елементами зовнішнього орієнтування, в процесі якого змінюється масштаб зображення і положення його елементів відносно координатних осей. Схожа задача виникає при внутрішньому орієнтуванні цифрового зображення.

Вирішення багатьох фотограмметричних задач зводиться до взаємного співставлення між собою зображень. Часто (наприклад в задачах моніторингу) співставляють знімки однієї і тієї ж території, отримані в різний час, з різних точок простору і навіть з допомогою різних знімальних систем. Для коректного співставлення зображень необхідно виконати деяку їх попередню обробку з метою приведення знімків до геометрії, придатної для якісних вимірювань та інтерпритації.

Згадаємо причини виникнення геометричних деформацій зображень, отримуваних фотографічними знімальними ситемами. Наприклад, коли рухома камера фіксує яскравісний

2

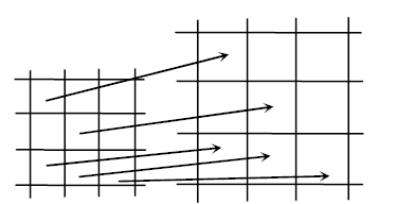
образ спостережуваного об’єкта (оптичну поверхню) в виді послідовних зображень, то цей образ від знімка до знімка деформується внаслідок перспективних спотворень і зміни положення камери. Геометрія відповідних деформацій моделюється проективними перетвореннями, які є доповненням відомих перетворень евклідової геометрії (пригадайте, що довжини і кути в проективній геометрії не зберігаються, а паралельні лінії можуть перетинатись).

Загалом геометричні перетворення можна поділити на прості, потребуючі зміни тільки геометричного розрізнення, і складні, в результаті яких відбувається зміна масштабу і поворот зображення в площині чи просторі.

Прості перетворення виконуються при зміні масштабу зображення шляхом зміни геометричного розрізнення, коли кожному пікселу вхідного зображення відповідає піксел перетвореного з таким самим або іншим геометричним розрізненням. При цьому формується нова матриця, елементам якої присвоюється радіометричне розрізнення відповідного йому вхідного зображення (рис. 2).

Рис. 2. Прості геометричні перетворення

Складні перетворення виконуються при трансформуванні зображення, коли коефіцієнт збільшення різних його частин неодинаковий, або коли виконується розворот на деякий кут. Перша ситуація виникає при відтворенні, наприклад, сітки квадратів за її перспектою, а друга

– при внутрішньому орієнтуванні знімка. В обох випадках (рис.2) кожному пікселу створюваного зображення відповідає декілька пікселів або їхніх частин вхідного зображення, або навпаки.

Сутність виконуваних при цьому геометричних і оптичних перетворень можна бачити на рис. 3, де елементи рядків і стовпців вхідного зображення позначені цифрами 1, 2, 3 та літерами a, b, c. Відповідні елементи створюваного зображення позначені – цифрами 1′, 2′, 3′ та літерами a′, b′, c′.

3

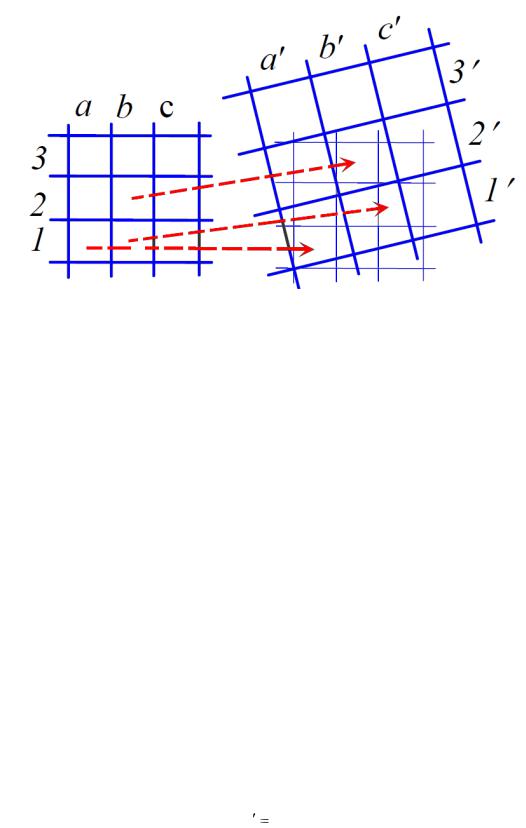
Рис. 3. Складні геометричні перетворення

Сумістимо ліві нижні кути зображень і згідно з рисунком побачимо, що елементу 1′a′ відповідними є фрагменти чотирьох елементів вхідного растру: 1a (45 %), 1b (35 %), 2a (15 %) та 2b (5 %). У такому випадку оптична щільність ρ′ створюваного елемента 1′a′ залежить від оптичних щільностей ρ1a, ρ1b, ρ2a, ρ2b елементів 1a, 1b, 2a, 2b. Причому

ρ′ = 0,45ρ1a + 0,35ρ1b + 0,15ρ2a + 0,05ρ2b.

Координати елемента створюваного зображення знаходять за координатами відповідного йому елемента вхідного зображення, підставляючи їх в потрібну формулу перетворення – трансформування координат точок нахиленого знімка, зв’язок координат точок знімка і місцевості, внутрішнього орієнтування знімка, або іншу.

ГЕОМЕТРИЧНІ ПЕРЕТВОРЕННЯ ЗОБРАЖЕНЬ

2.1. Геометричні перетворення на площині і в просторі

При вивченні геометричних перетворень плоских (тобто двомірних, або 2D) зображень, будемо вважати, что ми працюємо в евклідовому просторі, де існує ортонормована декартова система координат, в якій координатні осі взаємно ортогональні, а відповідні їм одиничні відрізки мають одинакову довжину. Тоді кожній точці зображення ставиться у відповідність впорядкована пара чисел (x,y) декартових координат: їх можна інтерпретувати як двовимірний вектор x, геометрично показаний відрізком прямої лінії з точки (0,0) в точку (x,y).

Вивчаючи двовимірні перетворення на площині нам особливо будуть цікавими лінійні перетворення, що представяються матрицями, тобто перетворення, при яких нові координати точки лінійно залежать від старих координат цієї точки наступним чином:

накладаються ті чи інші обмеження. Слід відразу зазначити, що кожному лінійному перетворенню (чи руху) на площині завжди знайдеться обернене, що переводить точки в

4

початкове положення, і любим двом послідовно виконаним перетворенням точок площини відповідає деяке третє перетворення, здійснююче аналогічну за результатом операцію. Прийнято говорити, що множина всіх лінійних перетворень формує загальну лінійну групу. Серед множини загальних лінійних перетворень нас цікавлять лиш деякі підгрупи. Перш за все, ми розглянемо матриці перетворення, пов’язані з найбільш важливими підгрупами загальної лінійної (чи проективної) групи, а саме евклідову підгрупу, а також підгрупи

подібності і афінну.

2.1.1. Точки і прямі лінії на площині - неоднозначності опису

Пряма лінія на площині, як відомо з аналітичної геометрії, складається з усіх точок, що задовольняють рівнянню

ax by 1 0

Нехай дві точки мають координати (x1 , y1 ) та (x2 , y2 ) відповідно. Яке рівняння лінії,

що їх з’єднує? Ясно, що оскільки лінія проходить через ці точки, то вона повинна задовільняти двом рівнянням

З іншого боку, якщо маємо дві лінії і потрібно знайти їх точку перетину (x, y) . Знову врахуємо відповідність рівнянням

Тут простежується важлива симетрія чи роздвоєність між проблемами перетину двох прямих і (з іншого боку) лінії, що проходить через дві задані точки. Параметри пари ліній і координати пари точок в обох випадках входять в формули одинаковим чином. Далі ми побачимо, що ця роздвоєність поширюється і на інші співвідношення між геометричними об’єктами.

Існує ряд проблем, пов’язаних із спеціальними співвідношеннями виділених пар точок і прямих. Вважатимемо, що координати двох точок відрізняються лиш скалярним множником: x2 x1 , y2 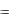y1 . Це означає, що x1 y2 x2 y1 0 і параметри прямої, з’єднуючої виділені

точки, визначити неможливо. Пряма лінія в даному випадку проходить через початок координат (0,0), что власне і створює проблему. Тут неможна безпосередньо використати рівняння прямої лінії (яка проходить через початок координат). Аналогічна проблема виникне, коли ми спробуємо з приведених вище рівнянь знайти точку перетину двох паралельних прямих, коли a2 a1 ,b2 b1 .

5

2.1.2. Однорідні координати

Для подолання відмічених проблем опису геометричних об’єктів, а також для вирішення задач перетворення 3D-простору і 2D-площини в одноманітному матричному виді вводиться формалізм так званих однорідних координат. Однорідними координатами служать

w 1

Очевидною властивістю однорідних координат є еквівалентність пари однорідних векторів, якщо один в інший переводяться посередництвом скалярного множника

Оскільки скалярний множник довільний, то однорідні координати в дійсності представляють лінію, що проходить через початок координат в евклідовому просторі. Прямі лінії на площині також можна представити 3-векторами в однорідних координатах:

, де c - довільний скалярний множник.

Видно, що як і для двох точок, однорідні координати двох ліній є еквівалентними, якщо відрізняються лиш спільним скалярним множником. Однорідні точки , що лежать

на однорідній лінії визначаються рівнянням або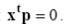 . Таким чином, точки і лінії мають тут одинакові представлення. Відмітимо, що прямим,

які проходять через початок в даному представленні відповідає значення с=0. Точка перетину двох паралельних прямих, що лежить в нескінченості, має множник w=0.

2.1.3. Евклідові перетворення

Сцену іноді можна розглядати як тверде тіло, коли взаємні деформації елементів сцени в тривимірному просторі не допускаються. Аналогічно і площину іноді можна вважати жорсткою (такою, що не деформується). Жорстким рухам площини відповідає евклідова підгрупа геометричних перетворень, яка містить лиш перетворення зсуву і повороту (рис.4), математично записуваних у векторно-матричній формі як

(3)

.

6

Рис.4. Дія евклідового перетворення на п’ять точок площини (зсув, поворот).

З допомогою трійок однорідних координат і матриць третього порядку можна описати будь-яке лінійне перетворення площини. Дійсно, введенням додаткової одиничної компоненти рівняння (3) можна переписати наступним чином:

(4)

відмітимо далі, що два послідовно проведені жерсткі рухи площини можуть бути представлені єдиним рухом:

переводить точки площини в початкове положення. Відміченою парою властивостей і характеризується група, а клас матриць із структурою виду (3) відомий як евклідова група перетворень. Матриці обертання R самі по собі формують так звану ортогональну підгрупу з важливою властивістю Rt R I , де І- одинична матриця.

2.1.4. Афінні перетворення

Якщо матрицю обертання в (2) замінити загальною невиродженою матрицею А , то отримаємо перетворення

x ax by c

або, в матричному виді

7

Рис.5. а) дія афінного перетворення на п’ять точок (зсув, поворот, зміна масштабів вздовж осей, косокутність із збереженням паралельних ліній);

б) вхідне зображення (ліворуч) і його афінно-перетворена копія (праворуч), отримана за рівнянням: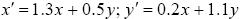

В однорідних координатах: (7)

Тут також передбачається, що визначник матриці перетворення не дорівнює нулю:

Рівняння (6),(7) визначають загальну форму запису афінного перетворення (див. рис.5). До будь-якого афінного перетворення існує зворотнє, яке також є афінним. Добуток прямого і зворотнього перетворень дає одиничне перетворення, яке залишає все на місці. Афінне перетворення є самим загальним взаємно однозначним відображенням площини на площину, при якому зберігаються прямі лінії. Зберігаються також відношення довжин відрізків, що лежать на одній прямій (або на паралельних прямих), і відношення площ фігур. Паралельні прямі переходять в паралельні.

В афінних перетвореннях площини особливу роль відіграють декілька важливих часткових випадків, які мають простий і наглядний геометричний смисл.

1.Розтягування (зтискання) вздовж координатних осей, задане у виді:

Розтягуванню вздовж відповідної осі відповідає значення масштабного множника, більшого за одиницю. В однорідних координатах матриця розтягу (стиску) має вид

8

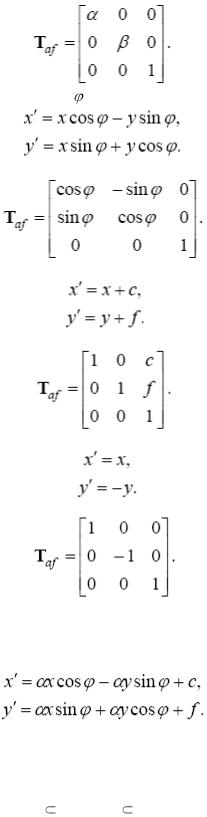
2.Поворот довкола початкової точки на кут , описується формулою:

Матриця обертання (для однорідних координат)

3.Перенос, який задається простими співвідношеннями:

Матриця переносу має вид

4.Відображення (відносно якоїсь з осей, наприклад осі абсцис) задається з допомогою формули:

Матриця відображення, відповідно

З аналітичної геометрії добре відомо, що будь-яке афінне перетворення (7) завжди можна представити у виді композиції послідовно виконуваних простіших перетворень означеного виду. Афінні перетворення утворюють афінну групу. Зокрема, підгрупою афінної групи перетворень є група подібності (містить перетворення зсуву, повороту і зміни масштабу):

В той же час афінна група є підгрупою загальної лінійної (проективної) групи, а евклідова група є частковим випадком афінної групи перетворень. Тому всі відмічені перетворення формують ієрархію згідно їх взаємної підлеглості

Евклідове перетвореня афінне проективне перетворення

Знаючи параметри афінного перетворення, можна розрахувати безпосередньо і параметри оберненого перетворення

9

розв’язавши систему рівнянь (5.5) відносно (x, y) :

Якщо параметри такі, що (1 a)(1 e) bd то дане афінне перетворення має нерухому точку (X 0 ,Y0 ) :

Зауважимо, що при x Ax, c 0 початок координат і буде нерухомою точкою.

2.1.5. Проективні перетворення

Як вже вище говорилось, загальними лінійними перетвореннями T (в представленні однорідними координатами)

(8)

формується група проективних перетворень (рис.6). При представленні в звичайних координатах, очевидно співвідношення (8) буде мати нелінійний вид, пов’язаний з перенормуванням

10