
ЛЕКЦІЯ_Моделі визначення координат за спостереженнями GNSS
.pdf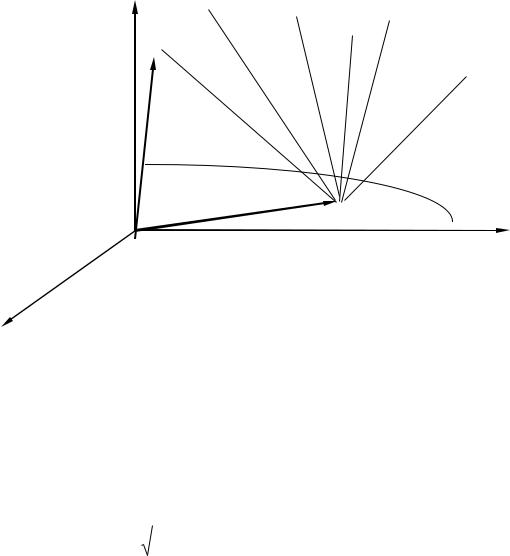
1
МОДЕЛІ ВИЗНАЧЕННЯ КООРДИНАТ ПУНКТІВ 2.1. Визначення координат пункту та поправки годинника приймача за виміряними псевдовідстанями (абсолютний спосіб)
З основного рівняння космічної геодезії для топоцентричного радіуса-вектора супутника r' запишемо:
r' = r - R , |
(2.1) |
де r і R - геоцентричні радіуси-вектори супутника і пункту спостереження, відповідно.
Z |
s2 |
s3 |
|
|
|
s5 |
|
|
s4 |
|
|
||
|
s1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
r3 |
r4 |
|
s6 |
|
|
|
|
|
|
r5 |
|
|
r1 |
|
|
|
|
r6 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
Y |
|
|
|
|
|
||
|
|
|
|
|
|
|
X Рис. 2.1. Схема абсолютного визначення координат пункту.
Відомо, що псевдовідстань - це модуль топоцентричного радіуса-вектора супутника |r'|, збільшений або зменшений (в залежності від знаку ) на величину добутку швидкості світла с та різниці поправок годинників супутників і приймача , а саме:
|
|
|
|
|
= r' + c , |
|
|
(2.2) |
|||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c . |
|
|
(2.3) |
||||
|
|
|
|
|
|
r R |
|
|
|||||
Через координати i-го супутника |
r, x , y , z та пункту R{X, Y, Z} вираз (2.3) прийме |
||||||||||||
|
|
|
|
i |
i i i |
|
|
|
|
|
|
||
наступний вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i |
|
xi X |
2 |
yi Y |
2 |
zi |
Z 2 c , |
(2.4) |
||||
Рівняння похибок для врівноважування координат пункту та поправки часу |
|
||||||||||||
запишемо як |
|
|
|
|
|
|
|
|
|
|
|
|
|
i X i Y |
i Z i |
i |
v |
, для i = 1, 2, ..., n , |
(2.5) |
||||||||
X |
Y |
Z |
|
|
i |
|
|
|
|||||
|
|
|
|
|
|
||||||||
де X, Y, Y i - відповідно поправки до координат пункту і до показів часу годинника приймача, vi - похибки, i - різниця між виміряною та обчисленою псевдовідстанню до i-го супутника, n - кількість виміряних псевдовідстаней (n 4). В рівнянні похибок (2.5) позначимо часткові похідні та вільний член рівняння відповідно через ai, bi, ci, di та li, і перепишемо його у звичному вигляді
ai X bi Y ci Z di li vi , для i = 1, 2, ..., n , (2.5')

2
Відзначимо, що в (2.5 ) порядок величин ai, bi, ci значно менший від порядку коефіцієнта di. При обчисленнях це приводить до великих похибок заокруглень і, відповідно, до зниження точності визначуваних параметрів, тобто поправок X, Y, Z i . Виходячи з цього, будемо шукати не саму поправку годинника приймача , а поправку її добутку на швидкість світла (c = 299792458 км/с), а саме t = c . Таким чином, визначаємо систематичну похибку геометричних відстаней від супутника до антени приймача, викликану похибкою годинника приймача, яка і перетворює відстані у псевдовідстані. Враховуючи вищезазначене, коефіцієнти та вільний член рівнянь похибок (2.5') будемо обчислювати за наступними формулами:
ai xi X 0
i
i обч.
; b |
yi Y 0 |
; |
c |
zi Z 0 |
||
i |
|
i |
|
i |
i |
|
|
|
|
|
|
||
|
li i вим. i обч. , |
|
||||

 xi X 0 2 yi Y 0 2 zi Z 0 2
xi X 0 2 yi Y 0 2 zi Z 0 2
;di 1 ,
c ,
(2.6)
(2.7)
(2.8)
де X0, Y0,Z0 - наближені координати пункту, ( i)вим. - виміряна псевдовiдстань.
Система нормальних рівнянь. У випадку, коли кількість виміряних псевдовідстаней (одночасно спостережених супутників) більше чотирьох (n>4) маємо перевизначену систему рівнянь. Щоб отримати однозначний розв'язок цієї системи, застосовують метод найменших квадратів, для цього систему рівнянь похибок виду
(2.5') перетворюють у систему нормальних рівнянь, яка має наступний вигляд: |
|
aa X ab Y ac Z ad t al 0 ; |
|
ab X bb Y bc Z bd t bl 0 ; |
(2.9) |
ac X bc Y cc Z cd t cl 0 ; |
|
ad X bd Y cd Z dd t dl 0 . |
|
У матричному записі система рівняннь похибок (2.5 ) матиме такий вид: |
|
AX L V . |
(2.10) |
Цій системі відповідатиме система нормальних рівнянь |
|
AT AX AT L 0 , |
(2.11) |
де А – матриця коефіцієнтів рівнянь похибок, X, L і V – вектори, відповідно, невідомих, вільних членів і похибок, символ Т – означає транспонування.
2.2. Визначення вектора між двома пунктами 2.2.1. Основні положення відносного способу визначення координат пункту
Мета визначення відносного місцеположення полягає у обчисленні координат невідомої точки відносно відомої, яка в переважній більшості застосувань залишається нерухомою. Іншими словами, визначення відносного місцеположення спрямоване на обчислення вектора між двома точками, який часто називають базою.
bAB
A B
Рис. 2.2. Визначення відносного місцеположення.
На рис. 2.2 точка А позначає опорну точку, точка В – невідому, а bAB – вектор бази. Вводячи відповідні вектори місцеположення ХА та ХВ , можна утворити співвідношення
X B X A b AB , |
(2.12) |
а формула для компонентів вектора бази bAB матиме вигляд
3
X B
b AB YB
Z B
X A |
X AB |
|
||||
Y |
|
|
|
Y |
. |
(2.13) |
|
A |
|
|
AB |
|
|
Z |
|
|
Z |
|
|
|
|
|
A |
|
|
AB |
|
Математичні моделі фазових відстаней можна застосувати в аналогічний спосіб з однією лише різницею, яка полягає у включенні відомих координат опорної точки. Ці координати повинні бути подані в системі WGS-84; досить часто вони є наближеним розв’язком на базі вимірів кодових відстаней.
Визначення відносного місцеположення найбільш ефективне, якщо здійснюється одночасні спостереження (супутників) як в опорній, так і в невідомій точці. Одночасність означає співпадання міток часу спостережень. Припустивши, що у двох точках А та В здійснюються такі одночасні спостереження супутників j та k. Тоді можна утворити лінійні комбінації – одиничні, подвійні, потрійні різниці тощо. Переважна більшість програм обробки застосовує ці різницеві методи, тому їх базові математичні моделі наведені в наступних підрозділах.
2.2.2. Рівняння фази
Частота електромагнітного сигналу f, яким є сигнал GPS, виражається через швидкість розповсюдження електромагнітних хвиль у вакуумі (c = 299792458 м c-1) і довжину хвилі сигналу як
f |
|
c |
. |
(2.14) |
||
|
||||||
|
|
|
|
|
||
Крім того, миттєва колова частота f є похідною від фази по часу |
|
|||||
f |
|
d |
. |
(2.15) |
||
|
||||||
|
|
dt |
|
|||
Звідси фазу можна отримати інтегруванням частоти в інтервалі часу від моменту t0 до t
:
t |
|
f dt . |
(2.16) |
t0
Якщо прийняти початкове значення фази t0 0 , то після подолання відстані від супутника до приймача рівняння фази прийнятого сигналу прийме вид
|
|
|
|
|
|
f t |
|
. |
(2.17) |
|
||||
|
|
c |
|
|
Під час спострежень приймач GPS генерує сигнал такої ж частоти, як і у прийнятого супутникового сигналу, і шляхом інтерференції утворює різницю фаз цих
електромагнітних хвиль, яка є виміряною фазою Rs t . З врахуванням похибок годиннників супутника s і приймача R рівнянням фази на основі виразу (2.15) буде
Rs t s t R t f |
|
f |
, |
(2.18) |
|
c |
|||||
|
|
|
|
де позначено s R . Зазначимо, що у приймачі вимірюється тільки дробова
частка миттєвої фази биття несучої хвилі, а початкове ціле число N повних коливань, які укладаються у відстань між супутником та приймачем, невідоме. Якщо спостереження від початкового моменту продовжуються безперервно, то число N, яке
4
називається цілочисловою невизначеністю, залишається незмінним, і фаза биття несучої хвилі в епоху t буде дорівнювати
Rs t f |
|
f N . |
(2.19) |
|
c |
||||
|
|
|
Підставляючи формулу (2.12) у рівняння (2.17) і позначаючи через отримаємо рівняння фазових псевдовідстаней
ij t |
1 |
ij (t) Nij f j i j (t) , |
|
|
|||
|
|
Фij Rs ,
(2.20)
де – вимірювана фаза несучої хвилі, в циклах, – довжина хвилі, а ij (t) – геометрична відстань між супутником та пунктом спостережень. Незалежна від часу фазова неоднозначність N ij є цілим числом, і тому її часто називають цілочисловою фазовою невизначеністю або цілочисловою невідомою. Величина f j позначає частоту
сигналу супутника в циклах за секунду (тобто виражену в герцах), а |
ij (t) – |
об’єднаний зсув годинників на супутнику та в приймачі. |
|
Величина об’єднаного зсуву ij (t) поділяється на дві частини за формулою |
|
ij (t) j (t) i (t) , |
(2.21) |
де та частина, що пов’язана з супутником відома з рівняння |
|
j (t) a0 a1 t t0 a2 t t0 2 , |
(2.22) |
де a0 , a1, a2 – три коефіцієнти полінома, які передаються за допомогою навігаційного повідомлення на опорну епоху t0 . Тому рівняння (2.22) дає можливість обчислити зсув супутникового годинника на епоху t . Невідомим в рівнянні (2.21) залишається член
i (t) , обумовлений приймачем.
Якщо рівняння (2.21) підставити у співвідношення (2.20), то модель фази набуває вигляду
ij (t) |
1 |
ij |
(t) Nij f j j |
(t) f j i (t) , |
(2.23) |
|
|
||||||
|
|
|
|
|
||
Припускаємо відомим зсув |
супутникового |
годинника j (t) |
(див. рівняння |
|||
(2.22)). Якщо кількість супутників становить n j , кількість епох – nt , то для окремого і кількість спостережень дорівнює n j nt . Кількості невідомих показані під відповідними членами правої частини наступного рівняння:
ij (t) f j j (t) |
1 |
ij |
(t) Nij f |
j i (t), |
||
|
||||||
|
|
|
|
(2.24) |
||
n j nt |
3 |
n j nt , |
||||
Розв’язання цього рівняння для окремої епохи (тобто nt 1) можливе лише за умови, що ми не звертаємо уваги на n j цілочислових невизначеностей. У цьому випадку
модель фазової відстані еквівалентна моделі кодової відстані і, отже, n j 4 . Отже
модель фази може бути використана для кінематичних застосувань, якщо неоднозначності отримати з початкових (наприклад, статичних) спостережень. Якщо знайти параметри неоднозначностей, то теоретично мінімальна кількість супутників
становить n j 2 . Це вимагає щонайменше nt 5 спостережних епох. Спостерігаючи
5
nt 4 супутників, можна отримати прийнятні результати. У цьому випадку потрібна кількість епох становить nt 3.
2.2.3. Обчислення різниць фаз.
Перші різниці. Розглянемо два пункти спостережень та один супутник. Позначаючи пункти як А та В, а супутник – як j і використовуючи рівняння (2.24), запишемо два рівняння фаз
Aj |
f |
j j (t) |
1 |
Aj |
(t) N Aj |
f j A (t), |
||||
|
||||||||||
|
|
|
|
|
|
|
|
(2.25) |
||
|
|
|
|
|
|
1 |
|
|
||
Bj f |
j j (t) |
|
Bj |
(t) N Bj |
f j B (t), |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
різниця між якими виражається формулою |
|
|
|
|||||||
Bj (t) Aj (t) |
1 |
Bj (t) Aj (t) N Bj N Aj f j B (t) A (t) , (2.26) |
||||||||
|
|
|||||||||
|
|
|||||||||
Рівняння (2.26) називається рівнянням перших різниць. З цього рівняння випливає один важливий аспект розв’язування відносно невідомих у правій частині. Система таких рівнянь призведе до дефіциту рангу навіть у випадках будь-якої надмірності вимірювань. Це можна побачити з коефіцієнтів неоднозначностей та зсувів годинників приймачів. В обох випадках однаковими є абсолютні значення коефіцієнтів для двох пунктів. Це означає, що твірна матриця вирівнювання містить лінійно пропорційні стовпчики і має дефіцит рангу. Тому введемо відносні величини
N ABj N Bj N Aj , (2.27)
AB (t) B (t) A (t).
Додатково використовуючи скорочені позначення
ABj |
(t) Bj (t) Aj (t), |
||
ABj |
(t) Bj |
(t) Aj |
(2.28) |
(t), |
|||
і підставляючи рівняння (2.27) та (2.28) у співвідношення (2.26), отримаємо остаточну форму рівняння перших різниць:
ABj |
(t) |
1 |
ABj |
(t) N ABj |
f |
j AB (t) . |
(2.29) |
|
|
||||||||
|
|
|
|
|
|
|
У порівнянні з рівнянням (2.24) зсув супутникового годинника у цьому випадку зникає. Другі різниці. Припустимо, що ми маємо два пункти (А та В) і два супутники (j,
k). Відповідно до рівняння (2.29) можна утворити два рівняння для перших різниць:
ABj |
(t) |
1 |
ABj (t) N ABj |
j AB (t), |
|
|
|||||
|
|
|
(2.30) |
||
|
|
1 |
|
||
kAB |
(t) |
kAB (t) N ABk |
k AB (t). |
||
|
|||||
|
|
|
|
Для того щоб отримати другі різниці, віднімемо ці перші різниці. Припускаючи рівність частот f j f k , дістанемо в результаті
kAB (t) ABj |
(t) |
1 |
kAB (t) ABj |
(t) N ABk |
N ABj . |
(2.31) |
|
|
|||||||
|
|
|
|
|
|
Використаємо скорочені позначення для супутників j та k, як у рівнянні (2.28), отримаємо кінцеву форму рівняння других різниць:
ABjk |
(t) |
1 |
kAB (t) N ABk . |
(2.32) |
|
|
|||||
|
|
|
|
6
Використовуючи другі різниці, досягаємо усунення зсувів годинників приймачів у випадку одночасності спостережень та еквівалентності частот сигналів супутників.
Введемо символічне позначення
ABjk |
kAB ABj , |
(2.33) |
де замість зірочки можна поставити параметри , , N . Зазначимо, що ці величини,
маючи два верхні та два нижні індекси, складаються в дійсності з чотирьох доданків. Символічне позначення
ABjk kB Bj kA Aj , |
(2.34) |
детально характеризує зв’язок величин у рівнянні подвійних різниць: |
|
ABjk (t) kB (t) Bj (t) kA (t) Aj (t), |
|
ABjk (t) kB (t) Bj (t) kA (t) Aj (t), |
(2.35) |
N ABjk N Bk N Bj N Ak N Aj . |
|
Треті різниці. До цього моменту ми розглядали лише одну епоху t. Для того щоб |
|
усунути незалежні від часу невизначеності, Remondi (1984) (див. [1]) запропонував утворювати різниці між другими різницями, сформованими для двох різних епох. При позначенні цих епох t1 і t2 рівняння двох других різниць матимуть вигляд
ABjk t1 |
1 |
ABjk t1 N ABjk , |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.36) |
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ABjk t2 |
ABjk t2 N ABjk , |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а їх різниця |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ABjk t2 ABjk |
t1 |
1 |
|
ABjk t2 ABjk |
t2 , |
(2.37) |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
є формулою третьої різниці. Її можна записати в спрощеному вигляді: |
|
||||||||||||||||||||||
ABjk t12 |
1 |
ABjk |
t12 , |
|
|
|
|
|
(2.38) |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
якщо використати для величин Ф і символічну формулу |
|
|
|
|
|
|
|
||||||||||||||||
t12 t2 t1 , |
|
|
|
|
|
|
(2.39) |
||||||||||||||||
Слід зазначити, що як ABjk t12 , так і ABjk |
t12 насправді містять вісім доданків кожна. |
||||||||||||||||||||||
Підставляючи рівняння (2.37) у вираз (2.34) чи (2.35), дістанемо в результаті |
|||||||||||||||||||||||
ABjk t12 kB t2 Bj t2 kA t2 Aj t2 |
|||||||||||||||||||||||
kB t1 Bj t1 |
kA t1 Aj t1 , |
|
(2.40) |
||||||||||||||||||||
|
|
||||||||||||||||||||||
та |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ABjk t12 kB t2 Bj t2 kA t2 Aj t2 |
|
||||||||||||||||||||||
k |
|
|
|
j |
|
|
|
|
|
k t |
|
|
j |
|
|
|
(2.41) |
||||||
t |
1 |
|
|
t |
1 |
1 |
t |
. |
|
||||||||||||||
B |
|
|
|
B |
|
|
A |
|
A |
|
1 |
|
|||||||||||
Треті різниці мають дві (пов’язані між собою) переваги, а саме: ефект усунення невизначеностей та несприйнятливість третіх різниць до змін невизначеностей, які називають стрибками фаз.
2.2.4. Кореляції комбінацій фаз.
Взагалі існують дві групи кореляцій: фізичні та математичні кореляції. Фази сигналу, який прямує від одного супутника, зареєстровані у двох точках, наприклад

7
ABj t і kAB t , фізично корелюють між собою, оскільки вони пов’язані з тим самим
супутником. Звичайно фізична кореляція не враховується. Тому головна увага приділяється математичним кореляціям, спричиненим утворенням різниць.
Можна припустити, що похибка фази є випадковою величиною, яка має
нормальний розподіл з нульовим математичним сподіванням і варіацією 2 . Тому виміряні (або необроблені) фази будуть лінійно незалежними чи некорельованими. Якщо ввести вектор , що містить фази, то коваріаційна матриця для фаз матиме вигляд
cov |
|
|
|
|
|
|
2 I |
, |
(2.42) |
||
де I – одинична матриця.
Перші різниці. Розглядаючи два пункти, А та В, та супутник j в епоху k, маємо
ABj (t) Bj (t) Aj (t) . (2.43)
Утворюючи другу першу різницю на ту саму епоху і для тих самих пунктів, але з іншим супутником k, отримаємо співвідношення
|
|
|
|
|
kAB (t) kB (t) kA (t) . |
|
|
|
|
|
|
|
|
(2.44) |
||||||||||||||||||||||||
Дві перші різниці можна обчислити з матрично-векторного співвідношення |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SD S , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.45) |
||||||||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
j |
(t) |
|
|
|
|
|
|
|
|
1 |
1 0 |
|
0 |
|
|
|
|
|
|
|
|
j |
|
|
|||||||||||
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
(t) |
|
|
|||||||||||||||
SD |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(2.46) |
|||||||||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
, |
k |
(t) |
|||||||||||||||||||||
|
|
k |
(t) |
|
|
|
|
|
|
|
0 |
|
0 1 |
1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
Закон перетворення коваріацій, застосований до рівняння (2.45), дає в результаті |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
cov |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
SD C cov C T . |
|
|
|
|
|
|
|
|
(2.47) |
|||||||||||||||||||||||
Підставляючи в рівняння (2.42), отримаємо коваріацію перших різниць у вигляді |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
cov |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
SD C 2 IC T 2 C C T . |
|
|
|
|
(2.48) |
|||||||||||||||||||||||||||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
cov |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
SD 2 2 I . |
|
|
|
|
|
|
|
|
(2.49) |
||||||||||||||||||
Це показує, що перші різниці не корелюють між собою. Слід зазначити, що розмір одиничної матриці у рівнянні (2.49) відповідає кількості перших різниць на епоху t, разом з тим множник 2 не залежить від кількості перших різниць. Якщо розглянути більш ніж одну епоху, то матриця коваріацій знову буде одиничною матрицею, розмір якої еквівалентний загальній кількості перших різниць.
Другі різниці. Тепер розглянемо три супутники j, k, l, серед яких j слугуватиме як опорний. Для двох пунктів А, В і епохи t з перших різниць можна утворити другі різниці
ABjk |
(t) kAB (t) ABj |
(t), |
||||||
ABjl |
(t) lAB (t) ABj |
(2.50) |
||||||
(t). |
||||||||
Ці два рівняння можна записати в матрично-векторній формі |
||||||||
|
|
|
|
|
|
|
|
|
|
DD C SD , |
(2.51) |
||||||
де введені позначення |
|
|
|
|
|
|
|
|

8
|
|
|
|
|
|
jk |
|
|
|
|
|
|
|
|
|
|
|
j |
(t) |
||
|
|
|
|
|
|
|
|
|
1 |
1 |
0 , |
|
|
|
|
AB |
|
|
|||
|
|
|
|
AB |
(t) |
|
|
|
|
|
|
|
k |
|
. |
||||||
DD |
, |
C |
SD |
(t) |
|||||||||||||||||
|
|
|
|
|
|
jl |
(t) |
|
|
|
|
|
0 |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
AB |
|
|
|
|
1 |
1 |
|
|
|
|
l |
(t) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матриця коваріацій других різниць виражається формулою cov DD C cov SD C T .
Підстановка рівняння (2.49) дає співвідношення
cov DD 2 2C C T ,
яке, використавши вираз для матриці C у формулі (2.52), запишемо у вигляді
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
cov DD 2 2 |
. |
|||||||
|
|
|||||||
|
|
|
|
|
1 |
2 |
||
Це показує, що другі різниці корелюють між собою. Вага, або матриця кореляцій отримується шляхом обернення матриць коваріацій за формулою
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
2 |
1 |
|
||
P(t) cov DD |
|
|
|
|
|
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
2 |
3 |
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
(2.52)
(2.53)
(2.54)
(2.55)
P(t) ,
(2.56)
в якій використані дві другі різниці на одну епоху.
Треті різниці. Рівняння третіх різниць дещо складніші, оскільки потрібно розглядати декілька різних випадків. Коваріацію окремої третьої різниці обчислимо шляхом застосування закону перетворення коваріацій до наступного рівняння:
ABjk t12 kAB t2 ABj |
t2 kAB t1 ABj |
t1 . |
(2.57) |
Тепер розглянемо дві треті різниці, утворені на одні і ті ж епохи та з одним супутником. Перша така різниця, що використовує супутники j, k, визначається за формулою (2.57). Друга третя різниця утворена відповідно для супутників j, l:
ABjk t12 kAB t2 ABj t2 kAB t1 ABj t1 ,
(2.58)
ABjl t12 lAB t2 ABj t2 lAB t1 ABj t1 .
Вводячи позначення
|
|
|
|
|
jk |
|
|
|
|
|
|
1 |
1 |
D D |
AB t12 |
|
, |
C |
|
|
|||||||
|
|
|
1 |
|
|||||||||
|
|
|
|
jk t |
12 |
|
|
|
|
|
0 |
||
|
|
|
|
|
AB |
|
|
|
|
|
|
||
0 |
1 |
1 |
1 |
|
|
|
|
ABj |
t1 |
|
|
|
|
|
|
kAB |
t1 |
|
|
|
|
|
|
|
|
||
1 0 |
|
|
|
lAB |
t1 |
|
|
SD |
|
||||||
, |
j |
t2 |
|
, |
|||
0 1 |
|
|
AB |
|
|
||
|
|
|
|
|
t2 |
|
|
|
|
|
kAB |
|
|
||
|
|
|
|
l |
|
|
|
|
|
|
AB |
t2 |
|
||
можна сформулювати векторно-матричне співвідношення
TD C SD .
Коваріацію третіх різниць отримаємо за допомогою перетворення cov TD C cov SD C T ,
яке шляхом підстановки рівняння (2.49) можна звести до вигляду cov TD 2 2C C T ,
(2.59)
(2.60)
(2.61)
(2.62)
Використовуючи формулу (2.59), дістанемо в результаті вираз матриці коваріацій для двох третіх різниць у вигляді (2.58):

9 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
cov TD 2 2 |
. |
(2.63) |
|||||
|
|
||||||
|
|
|
2 |
4 |
|
||
2.2.5. Статичний метод визначення відносного місцеположення пункту.
Під час геодезичної зйомки вектора окремої бази між пунктами А та В два приймачі повинні на протязі всієї спостережної сесії стояти стаціонарно. Нижче наводяться дослідження перших, других та третіх різниць щодо визначення кількості рівнянь спостережень та невідомих параметрів. Припустимо, що в пунктах А та В існує можливість спостерігати одні і ті самі супутники в одночасні епохи. Практична проблема затінення тих чи інших супутників тут не розглядаються. Кількість епох позначається як nt , а кількість супутників – як nj.
В рівнянні (2.24) (в якому супутниковий годинник за припущенням відомий), показано, що недиференційована фаза тут не включається, оскільки не існуватиме зв’язку між точками А та В. Можна отримати розв’язок для двох окремих наборів даних, що буде еквівалентно визначенню місцеположень окремого пункту.
Перші різниці можна виразити для кожної епохи та кожного супутника. Тому кількість вимірів становитиме nt nj. Кількість невідомих показана під відповідними доданками рівняння перших різниць (див. рівняння (2.29)):
j |
(t) |
1 |
j |
(t) N j |
f j |
(t), |
|
||||||
AB |
|
|
AB |
AB |
AB |
(2.64) |
|
|
|
|
|
n j nt 3 n j nt .
Відношення кількості рівнянь до кількості невідомих параметрів можна переписати відносно кількості епох у наступному вигляді:
nt |
n j 3 |
|
|
|
. |
(2.65) |
|
|
|||
|
n j 1 |
|
|
Якими є мінімальні теоретичні вимоги? Один супутник не забезпечує розв’язання, оскільки знаменник у формулі (2.65) стає нульовим. Для двох супутників дістанемо в
результаті nt 5 , а для нормального випадку чотирьох супутників – nt 73 , або відповідно після округлення до більшого цілого числа nt 3 .
Для других різниць відношення кількості вимірів та невідомих параметрів отримується з тих же міркувань. Слід зазначити, що для однієї другої різниці необхідно
два супутники. Тому для n j супутників кожної епохи утворюється n j 1 других різниць, так що загальна кількість других різниць становитиме n j 1 nt . Кількість невідомих знайдемо з рівняння (див. (2.32))
ABjk (t) |
1 |
ABjk (t) N ABjk , |
|
|||
|
(2.66) |
|||||
|
|
|
|
|||
n j 1 nt 3 n j 1 . |
|
|||||
або |
|
|
|
|
|
|
n |
n j |
2 |
|
|||
|
|
|
. |
(2.67) |
||
|
|
|
||||
t |
|
n j |
1 |
|
||
|
|
|
||||
Отже, мінімальна кількість супутників становить два, що дає в результаті nt 4 . У
випадку чотирьох супутників потрібно дві епохи. Для того щоб уникнути лінійної залежності рівнянь під час утворення других різниць, використовується опорний супутник, дані якого віднімаються від вимірів усіх інших супутників. Наприклад, візьмемо випадок коли спостерігаються супутники 6, 9, 11, 12, а 6-ий використовується
10
як опорний. Тоді для кожної епохи можна утворити наступні другі різниці: (9-6), (11-6), (12-6) тощо. Інші другі різниці будуть лінійними комбінаціями і тому лінійно залежними між собою.
Математична модель третіх різниць включає лише три невідомі координати пункту. Для утворення окремої третьої різниці потрібно дві епохи. Далі, у випадку
кількості nt епох можливе утворення |
|
n j 1 лінійно незалежних комбінацій епох. |
|||||||||||
Отже, в результаті дістанемо рівняння |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
jk t |
|
|
1 |
|
jk |
t |
, |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
AB |
12 |
|
|
|
AB |
12 |
|
(2.68) |
|||
|
|
n j 1 n j 1 3. |
|
|
|||||||||
Співвідношення між кількістю рівнянь та невідомих можна записати у вигляді |
|||||||||||||
|
|
|
|
n |
n j |
2 |
. |
|
(2.69) |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
t |
|
n j |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Ця |
нерівність дає |
nt 4 епох, якщо |
|
підставити |
мінімальну кількість |
супутників |
|||||||
n j |
2 . Для n j 4 |
супутників потрібна кількість епох становитиме nt 2 . |
|||||||||||
2.5. Виявлення та відновлення стрибків фази.
Означення стрибків фази.
Під час спостережень приймач реєструє дробову частину фази биття (тобто різницю між переданою супутником несучою хвилею та сигналом-копією, згенерованою приймачем), а лічильник цілих циклів розпочинає відлік. Лічильник збільшує показ на одиницю кожного разу, коли фаза змінюється від 2 до 0. Отже, на задану епоху спостережувана накопичена фаза є сумою показів відліків дробової
частини фази та цілочислового лічильника п. Початкова ціла кількість циклів N, яка
відповідає відстані між супутником та приймачем, невідома. Ця невизначеність фази N залишається сталою до того моменту, поки не буде перерви у стеженні. Якщо це станеться, то цілочисловий лічильник знову починає відлік, що спричиняє стрибок миттєвої накопиченої фази на цілу кількість циклів. Цей стрибок називається стрибком фази і, звичайно, має місце лише в фазових вимірах.
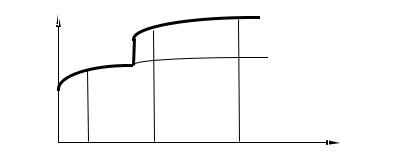
Фаза
Час
ti |
ti+1 |
ti+2 |
Рис.2.1. Графічне відображення стрибків фази.
Графічно сирибок фази відображений на рис. 2.1. Якщо накреслити залежність вимірюваної фази від часу, то ми повинні отримати досить гладку криву. У випадку стрибка фази на кривій графіка з’являється несподіваний різкий розрив.
Розрізняють три джерела стрибків фази, а саме:
Перешкоди на шляху розповсюдження супутникового сигналу через дерева, будинки, мости, гори тощо.
