
Дульцев Форма орбіти та рух ШСЗ за законами Кеплера
..pdfМIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНIВЕРСИТЕТ "ЛЬВIВСЬКА ПОЛIТЕХНIКА"
ФОРМА ОРБІТИ ТА РУХ ШСЗ ЗА ЗАКОНАМИ КЕПЛЕРА
МЕТОДИЧНI ВКАЗIВКИ
до лабораторної роботи з курсу “Супутникова геодезія” для студентів базових напрямів „Геодезія, картографія та землевпорядкування”
Затверджено на засіданні кафедри вищої геодезії та астрономії, протокол № 6-02/03 від 15.01.2003 р.
Львів 2003
Форма орбіти та рух ШСЗ за законами Кеплера: Методичні вказівки до лабораторної роботи з курсу “Супутникова геодезія” для студентів базових напрямів: „Геодезія, землевпорядкування та кадастр” і „Фотограмметрія” інституту геодезії та геоінформатики /Автори: А.Т. Дульцев, I.М. Цюпак, Л.М. Янків-Вітковська.- Львів: Видавництво Національного університету “Львівська політехніка”, 2003.- 16 с.
Автори |
Дульцев А.Т., канд.техн.наук, доц. |
|
Цюпак І.М., канд.техн.наук, доц. |
|
Янків-Вітковська Л.М., канд.фіз.-матем.наук, доц. |
Відповідальний за випуск |
Заблоцький Ф.Д., д-р техн.наук, доц. |
Рецензенти |
Двуліт П.Д., д-р техн.наук, проф. |
|
Костецька Я.М., д-р техн.наук, проф. |
Мета роботи: ознайомити студентів з теоретичними основами руху ШСЗ за законами Кеплера; навчити їх виконувати обчислення основних параметрів, що характеризують орбіту ШСЗ.
Лабораторна робота виконується індивідуально за вихідними даними свого варіанту завдання, виданого викладачем. До роботи необхідно зробити рисунки, записати робочі формули, результати обчислень навести після підстановки значень у формули.
1. Теоретичні відомості
Використання штучних супутників Землі (ШСЗ) (з 4 жовтня 1957 року) для наукових і науково-технічних задач геодезії стало початком створення космічної геодезії. Космічна геодезія дає можливість в короткі терміни і з більшою точністю, ніж традиційні методи, розв’язувати задачі геодезії.
Якщо розглядати методи космічної геодезії в послідовності їх розвитку, то першим вважається геометричний метод, суть якого у синхронному фотографуванні ШСЗ на фоні зоряного неба мінімум із двох пунктів на поверхні Землі. Така організація спостережень дозволяє визначити напрям вектора, що з’єднує ці пункти. Множина таких векторів утворює векторну просторову мережу – космічну тріангуляцію. Наступний, найбільш загальний метод – динамічний, який базується на вивченні еволюції орбіти ШСЗ в часі для визначення динамічних параметрів, якими є параметри гравітаційного поля Землі (геопотенціалу). При цьому одночасно визначаються координати пунктів спостереження у єдиній геоцентричній системі координат (земній або гринвіцькій). В орбітальному методі за допомогою вимірів, зроблених на наземних пунктах чи безпосередньо із супутника, визначаються координати пунктів і елементи орбіт.
Рух супутника в просторі визначається такими факторами: притяганням гравітаційних полів Землі, Місяця, Сонця та інших планет Сонячної системи, місячно-сонячними припливами, тиском сонячного світла, гальмуванням в атмосфері, дією магнітного поля Землі та іншими. З перелічених факторів вплив гравітаційного поля Землі є домінуючим, тому у першому наближенні, розглядаючи рух ШСЗ, дією інших факторів можна знехтувати.
Якщо ж прийняти, що тіло Землі має сферичну форму з рівномірним розподілом масс в сереюдині, то у цьому випадку притягання Землі відповідає притяганню матеріальної точки, масса якої дорівнює масі Землі. Рух супутника довкола такої планети, при відсутності інших факторів, відбувається за законами Кеплера, і його називають незбуреним або кеплеровим.
Нехай маємо геоцентричну інерціальну систему координат: початок – у центрі масс Землі, вісь Oz співпадає із середньою віссю обертання Землі у просторі, вісь Ox – у напрямку середньої точки весняного рівнодення , вісь Oy – лежить у площині середнього екватора на 90 на схід від осі Ox. Нагадаємо, що точка весняного рівнодення є точкою перетину небесного меридіана з екліптикою. Екліптика – це видимий річний рух Сонця по небесній сфері, тобто це приблизно осереднена орбіта Землі навколо Сонця.
Диференціальні рівняння незбуреного руху ШСЗ на основі законів ньютонівської механіки. На основі другого закону Ньютона вектор сили F дорівнює
F m r , |
(1) |
де r - вектор прискорення супутника, m – його маса. Модуль сили F згідно із законом всесвітнього тяжіння буде
|
F |
|
f |
M m |
, |
(2) |
|
|
|||||
|
|
r 2 |
||||
|
|
|
|
|
|
де f – гравітаційна стала, r – відстань від центра маси Землі M до супутника m. Вектор сили взаємодії Землі і супутника, виходячи із закону (2), виразиться так:
F f |
M m |
|
r |
. |
(3) |
r 2 |
|
||||
|
|
r |
|
||
Тут r – вектор положення супутника, а його складовими у прийнятій геоцентричній системі - є координати ШСЗ, тобто
x
r y . (4)
z
Прирівнюючи праві частини формул (1) і (3), отримаємо диференціальні рівняння
незбуреного руху ШСЗ у векторній формі: |
|
|
||
r |
|
r , |
(5) |
|
r 3 |
||||
|
|
|
||
де fM – гравітаційний параметр Землі. Диференціальні рівняння (5) в координатній формі мають вид
|
|
x |
|
d |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||
|
|
|
dt 2 |
r 3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
d |
2 |
y |
|
|
|
|
|
|
|
||
|
|
y |
|
|
|
y , |
|
(6) |
||||||||
|
|
dt 2 |
|
r 3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
z |
d |
2 |
z |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z |
|
|
||||||||
|
|
|
|
|
|
|
r 3 |
|
|
|||||||
|
|
|
|
|
dt 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де x , |
y |
|
|
|
|
|
|
|
|
|
супутника. Інтегруванням диференціальних |
|||||
і z – складові вектора прискорення r |
|
|||||||||||||||
рівнянь руху ШСЗ прогнозується його положення, |
вектор r (див. (4)), і складові x , |
y , |
z |
|||||||||||||
|
на інші моменти часу відносно початкового моменту t0. |
|
||||||||||||||||||||||
вектора швидкості r |
|
|||||||||||||||||||||||
Інтегрування диференціальних рівнянь руху. Інтегрування системи трьох рівнянь |
||||||||||||||||||||||||
другого порядку дає наступний загальний розв’язок: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x x t, c1, c2 , c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, c2 , c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y y t, c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
, c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
z t, c1, c2 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
(7) |
||||||||
|
x x t, c , c |
|
|
, c |
|
|
, c |
|
|
|
, c |
|
|
, c |
|
|
|
|
||||||
|
2 |
3 |
4 |
|
5 |
6 |
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y y t, c , c |
|
, c |
|
|
, c |
|
|
, c |
|
|
, c |
|
|
|
|
|
|||||||
|
2 |
3 |
4 |
5 |
6 |
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
z z t, c , c |
2 |
, c |
3 |
, c |
4 |
, c |
5 |
, c |
6 |
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
де t – час, с1, с2, с3, с4, с5, с6 – довільні сталі, які визначаються початковими умовами руху. Ними є параметри орбіти ШСЗ x0 , y0 , z0 , x0 , y0 , z0 на початковий момент t0.
Інтегрування диференціальних рівнянь(5) або (6) виконують різними способами [ ].
Інтеграли площ. Якщо рівняння руху (5) помножити векторно на r, отримаємо
|
|
|
|
r r 0 . |
(8) |
||
|
|
|
|||||
r 3 |
|||||||
r r |
|||||||
Це рівняння тотожне наступному: |
|
|
|
|
|
||
|
d |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
dt r r 0 . |
(9) |
|||||
Інтегруючи рівняння (9) отримаємо |
|
|
|
|
|
||
|
|
|
r r c , |
(10) |
|||
де стала інтегрування с є інтегралом площ у векторній формі. Векторний добуток (10) у матричній формі має такий вид:
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
x |
y |
z |
|
ic1 |
jc2 kc3 , |
(11) |
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
де с1, с2, с3 – складові вектора с, а |
i, |
j, |
|
k – |
одиничні вектори – |
орти відповідних осей |
координат. Викреслюючи перший рядок матриці в (11) і стовпчик відповідного орта, отримаємо визначники другого порядку, обчислюючи котрі, маємо три інтеграли площ в координатній формі
yz zy c1 , |
zx xz c2 , |
xy yx c3 . |
(12) |
||||||
Назва інтеграла площ походить від сутності векторного добутку, результатом котрого є |
|||||||||
|
|
і |
|
r |
|
. Напрям вектора с |
|||
вектор с, модуль якого дорівнює площі паралелограма зі сторонами |
r |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
перпендикулярний до площини, в якій лежать вектори r і r .
Інтеграл енергії. Векторне диференціальне рівняння незбуреного руху (5) помножимо
скалярно на 2r , маємо
2r r |
2 |
r r . |
|||||||||||||
r 3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ліва частина рівняння (13) тотожна виразові |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
d |
|
|
|
2 |
|
|
|||
|
|
dt V |
|
. |
|||||||||||
|
2r |
r |
|
||||||||||||
Крім того, має місце тотожність |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r r r r . |
||||||||||||
Підставляючи (14) і (15) у (13), отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
|
2 |
|
|
|
|
|
2 |
|
|
|||
|
dt V |
|
r 2 |
||||||||||||
|
|
|
r . |
||||||||||||
Відомо, що |
d 1 |
|
|
r |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
r 2 |
|
|||||||
|
|
|
dt r |
|
|
|
|
|
|||||||
Підставивши тотожність (17) в рівняння (16) і про інтегрувавши, маємо
(13)
(14)
(15)
(16)
(17)

V 2 |
2 |
h , |
(18) |
|
r |
||||
|
|
|
||
де h – стала інтегрування. |
|
|
|
|
Величина V2 пропорціональна кінетичній |
енергії системи, а 2 r |
характеризує |
||
потенціальну енергію. Таким чином, V 2 2 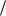 r h характеризує сталість алгебраїчної суми кінетичної і потенціальної енергій для даної системи.
r h характеризує сталість алгебраїчної суми кінетичної і потенціальної енергій для даної системи.
Інтеграли Лапласа. Диференціальні рівняння незбуреного руху помножимо векторно на вектор інтеграла площ с
|
|
r c . |
(19) |
|
c r 3 |
||||
r |
Інтеграл площ с згідно з (10) є результатом векторного добутку векторів r і r . У правій частині виразу (19) замінимо вектор с, отримаємо
|
|
r r r 0 . |
(20) |
r c r 3 |
|||
|
|
|
|
Векторний добуток трьох векторів можна замінити на скалярний відповідно до правила a b c b a c c a b .
Зробимо таку заміну в рівнянні (20), маємо
|
r 3 |
r r r |
r r r r c 0 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Після перетворень запишемо |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
r r r r |
r c 0 . |
|||||||
|
|
|
r 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Отриманий вираз тотожний наступному: |
|
|
|
|||||||||
|
|
|
|
d |
|
|
r |
|
|
0 . |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
r c |
||||||
|
|
|
|
|
dt |
|
r |
|
|
|
||
Інтегруючи вираз (21), отримаємо інтеграл Лапласа у векторній формі
|
r |
r c f , |
|
r |
|||
|
|
(21)
(22)
де f – стала інтегрування. Вираз (22) можна записати у виді, що розкриває векторний добуток
|
|
i |
j |
k |
|
|||
|
|
|
|
|
|
|
|
|
|
xi yj zk x |
y |
z |
|
f1i f 2 j f3k . |
|||
|
r |
c |
c |
|
c |
|
|
|
|
|
2 |
3 |
|
||||
|
|
1 |
|
|
|
|
||
Записуючи векторний добуток через визначники і прирівнюючи вирази при однакових ортах, отримаємо рівняння для вектора Лапласа в координатній формі
r x c3 y c2 z f1 ,

|
y c z c |
3 |
x |
f |
2 |
, |
(23) |
||||
|
r |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z c |
2 |
x c y |
f |
3 |
. |
|
||||
|
r |
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Формулами (12), (18) і (23) записані сім перших інтегралів рівнянь незбуреного руху ШСЗ – три інтеграли площ, три інтеграли Лапласа та інтеграл енергії. Вони не можуть бути загальним розв’язком тому, що не містять явно час і не є незалежними.
Існує залежність між інтегралами площ і Лапласа, яка виражається наступним рівнянням:
f c 0 , |
(24) |
яке свідчить про ортогональність (перпендикулярність) цих двох векторів. Усі сім сталих зв’язує інше рівняння
|
|
|
f 2 2 |
hc2 , |
|
(25) |
|||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f f 2 |
f 2 |
f 2 |
; |
c c2 |
c2 |
c2 . |
|||
1 |
2 |
3 |
|
1 |
2 |
3 |
|
||
Дослідження незбуреного руху. Якщо векторне рівняння інтегралу площ (10) скалярно
помножити на вектор r і здійснити перетворення, отримаємо вираз |
|
r c 0 , |
(26) |
яке виявляється рівнянням площини, що проходить через початок координат. В координатній формі воно має такий вид:
c1x c2 y c3 z 0 . |
(27) |
Рівняння (26) або (27) показує, що незбурений рух супутника відбувається у незмінній площині, яка визначається тільки початковими умовами задачі і, як наслідок, орбіта ШСЗ є плоскою кривою. Звідси, незбурений рух відбувається у площині, яка перпендикулярна (ортогональна) до вектора площ с. З математики відомо, що положення площини у просторі визначається перпендикулярним (ортогональним) до неї вектором. Таким чином, вектор площ с визначає орієнтацію площини орбіти супутника у просторі.
Тепер на вектор r помножимо скалярно вектор Лапласа (22), зробимо перетворення і отримаємо таке рівняння:
r c2 f r , |
(28) |
|
а у координатній формі воно має такий вид: |
|
|
r c2 |
f1x f2 y f3 z . |
(28 ) |
Рівняння (28) або (28 ) описує поверхню, на якій знаходиться супутник під час руху. Ця поверхня є поверхнею другого порядку, утвореною обертанням навколо осі, яка задана вектором f, один з фокусів якої співпадає з початком координат. Це може бути еліпсоїд, параболоїд або гіперболоїд обертання. Розв’язок системи складеної з рівнянь (27) і (28 )
c1x c2 y c3 z 0
(29)
r c 2 f1x f 2 y f3 z 0
геометрично є січення поверхні обертання площиною. В результаті січення виходить плоска крива другого порядку.
Згідно з першим законом Кеплера, незбурена орбіта супутника є плоскою кривою другого порядку, в одному з фокусів якої знаходиться центральне тіло (для штучних супутників Землі центральним тілом є Земля). В залежності від ексцентриситету орбіта супутника може приймати форму однієї з наступних плоских кривих другого порядку:
- кола, якщо ексцентриситет |
е = 0; |
|||
- еліпса, |
- « - |
0 |
< е < 1; |
|
- параболи |
- « - |
|
е = 1; |
|
- гіперболи |
- « - |
|
е > 1. |
|
Найчастіше орбіта ШСЗ є еліпсом. У цьому випадку форма, розміри, орієнтація орбіти |
||||
супутника визначається 6-ма параметрами (елементами орбіти ), а саме : |
||||
a |
- велика піввісь орбіти, |
|
|
|
e |
- ексцентриситет орбіти, |
|
||
Ω - довгота висхідного вузла орбіти, |
||||
i |
- кут нахилу орбіти, |
|
|
|
ω - аргумент перицентру, |
|
|
||
- момент проходження через перицентр.
|
|
|
|
|
|
A |
|
v |
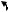
 П
П
x J2000.0 |
|
Рис. 1. Елементи орбіти.
Розміри і форма орбіти задаються великою піввіссю а та ексцентриситетом е орбіти. Орієнтація площини орбіти в просторі визначається довготою висхідного вузла орбіти Ω і кутом нахилу i.
Орбіта супутника перетинає небесний екватор у двох точках. Ці точки називаються вузлами:
-висхідний, в якому супутник перетинає екватор рухаючись з південної півкулі в північну;
-низхідний, в якому ШСЗ перетинає екватор рухаючись з північної півкулі в південну. Довгота висхідного вузла орбіти вимірюється від точки весняного рівнодення по екватору
від 0 до 360 , а кут нахилу і від площини екватора зі сходу на захід через точку півночі від 0
до 180 .
Аргумент перицентру (для ШСЗ - перигею) ω орієнтує велику вісь орбіти (лінію апсид, що з’єднує точки а п о г е ю і п е р и г е ю) в її площині, і вимірюється від точки висхідного вузла по орбіті від 0 до 360 . Апогей є найвіддаленішою точкою орбіти від Землі, а перигей – найближчою.
Положення супутника на орбіті визначається кутовим параметром v - істинною аномалією – кутом між напрямом на перигей і на положення супутника (див. рис. 1).
Пряма, що з’єднує фокуси, тобто лінія апсид, співпадає з напрямком вектора Лапласа, а вектор площ перпендикулярний до площини орбіти (рис. 2).
|
|
c |
|
|
A |
F2 |
F1 |
|
П |
|
|
f |
||
|
|
|
|
r
m
Рис. 2. Орбіта ШСЗ із взаємним розміщенням векторів r, c і f.
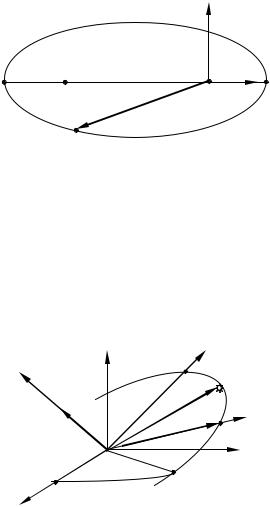
Рух супутника на орбіті визначається другим і третім законами Кеплера. У другому законі Кеплера зазначається, що за рівні проміжки часу радіус-вектор супутника описує площі рівних секторів. Інакше кажучи, що секторіальна швидкість супутника є стала. Це можна довести, якщо розглядати рух ШСЗ у системі координат O , жорстко скріпленій з площиною орбіти (рис. 3). Дві осі, О і O лежать у площині орбіти, тоді третя O – направлена перпендикулярно до площини орбіти по вектору інтеграла площ с. Вісь О направлена у точку перигею.
|
z |
|
|
|
|
|
|
|
|
|
|
c |
r |
|
|
|
f |
|
|
|
|
П |
|
|
|
|
|
|
O |
|
y |
|
|
N |
|
x |
|
|
|
Рис. 3. Зв’язок систем координат O і Oxyz.
У вибраній орбітальній системі координат (рис. 3) інтеграли площ отримаємо з виразу
i |
|
|
|
|
|
|
|
|
j |
k |
|
|
|||
|
|
|
|
|
|
|
|
r r |
|
|
0 |
|
i 0 j 0 k c , |
(30) |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
де i , j , k - орти відповідних осей орбітальної системи координат. Розкриваючи визначник і прирівнюючи вирази при однакових ортах, отримаємо
|
(31) |
c . |

Введемо полярну систему координат у площині орбіти через радіус-вектор r і кут v, і в цій системі координат виразимо інтеграл площ (31). Для цього знайдемо вирази для координат, і складових вектора швидкості , супутника у площині орбіти
r cosv , |
|
|
r cos v r sin v v , |
|
|
r sin v , |
r sin v r cosv v . |
(32) |
Тепер підставимо вирази (32) у формулу (31) для вектора площ і після перетворень отримаємо
r 2 v c . |
(33) |
||||||||
Нехай положення супутника за невеликий проміжок часу t зміниться на кут |
v. Тоді |
||||||||
площа, яку опише радіус-вектор супутника, буде площею сектора |
|
||||||||
|
|
|
r 2 |
|
|||||
s |
|
|
|
v . |
|
||||
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
||
Похідну від площі по часу t називають секторіальною швидкістю, яка запишеться так |
|||||||||
s |
ds |
|
|
1 |
r 2v . |
(34) |
|||
|
|
|
|||||||
|
dt |
2 |
|
|
|||||
Порівнюючи формули (33) і (34), маємо |
|
|
|
|
|
|
|
||
|
s |
c |
, |
(35) |
|||||
|
|
||||||||
|
|
|
2 |
|
|
|
|||
що виражає другий закон Кеплера.
Рівняння орбіти в полярних координатах. Розв’язок системи рівнянь (29) є рівнянням орбіти. В орбітальній системі координат система (29) перетворюється у таку:
0 |
|
|
r c 2 |
. |
(36) |
f 0 |
|
|
|
|
|
В полярних координатах друге рівняння системи (36) після |
підстановки r cosv |
||||||
прийме вид |
|
|
|
|
|
||
|
|
c2 |
|
|
|
||
r |
|
|
|
|
. |
|
|
1 f |
cos v |
|
|
||||
Якщо позначити |
|
|
|
|
|
||
c2 p ; |
f e |
, |
(37) |
||||
отримаємо рівняння кривої другого порядку у полярних координатах |
|
||||||
|
|
|
p |
|
|
||
r |
|
, |
|
(38) |
|||
1 e cos v |
|
||||||
де p – параметр кривої, е – ексцентриситет. Параметр |
орбіти |
(для еліптичного руху – |
|||||
фокальний параметр) можна виразити через велику піввісь орбіти |
|
||||||
p a 1 e2 . |
|
(39) |
|||||
В залежності від ексцентриситету е плоска крива другого порядку може приймати різну форму і значення інтегралів c, f i h при цьому також змінюються. Дослідимо, які значення
