Тема 2 Похибки вимірювань

рис. 8. Похибка має такий закон розподілу, якщо вона утворюється з двох незалежних складових, кожна із яких має рівномірний закон розподілу, але з різною шириною своїх інтервалів. При послідовному з'єднанні двох вимірювальних перетворювачів, один із котрих має похибку, рівномірно розподілену в інтервалі ±Δх1, а інший – похибку, рівномірно розподілену в інтервалі ±Δх2, загальна похибка перетворення буде описуватись трапецієподібним законом розподілу. Трикутний закон розподілу є частковим випадком трапецієподібного, коли х1 = х2.

Рисунок 8 – Диференційна функція трапецієподібного закону розподілу похибок

Ці три закони розподілу мають обмежене застосування при оцінюванні результатів вимірювань, оскільки переважно похибки виникають через вплив великої кількості причин. У таких умовах розподіл похибок найкраще узгоджується з нормальним законом розподілу.

Нормальний закон розподілу (закон розподілу Гаусса). Цей закон є одним із найпоширеніших законів розподілу похибок, що пояснюється центральною граничною теоремою теорії ймовірностей, яка твердить, що розподіл випадкових похибок буде близьким до нормального, якщо результати спостереження формуються під впливом великої кількості незалежних факторів впливу, кожний із котрих створює лише незначну дію порівняно з сумарною дією всієї решти.

Нормальний закон має такий вираз для диференційної функції розподілу:

із рівняння можна зробити висновок:

1.Густина ймовірностей має максимум при х = М[х];

2.Із збільшенням похибки = х – М[х] незалежно від знака (функція парна) густина ймовірності прямує до нуля;

3.Із збільшенням середнього квадратичного відхилення ймовірність більших відхилень зростає, тобто розміри розсіюються в ширшому інтервалі.

Необхідно зауважити, що незважаючи на широке застосування нормального розподілу, він все-таки є лише моделлю реальних розподілів. До речі, він відмінний від нуля вздовж всієї нескінченності осі. Тому нормально розподілена випадкова величина, хоч із малими ймовірностями, але може приймати які завгодно великі значення. Хоча очевидно, що всі вимірювані фізичні величини завжди обмежені за абсолютним значенням.

Розподіл Релея. Цей розподіл має модуль двовимірного вектора, координати котрого розподілені нормально відносно нульових математичних сподівань і однакових дисперсій

M x M y 0; r x2 y2 ; x y

Розподіл Релея зручний для апроксимації розподілу контрольованих показників, котрі можуть бути лише з однаковим знаком. Наприклад, при контролі відхилення форми і розміщення осей та поверхонь деталей, як овальність, конусність, радіальне биття, відхилення від співосності, паралельності, перпендикулярності тощо можна описати тільки таким розподілом.

6. ОБРОБКА РЕЗУЛЬТАТІВ ВИМІРІВ

Точкові оцінки результатів вимірювання.

Точковими називаються оцінки, що виражаються одним числом. До таких оцінок відносяться: середнє арифметичне або середнє зважене, дисперсія, середня квадратична похибка. У практиці товарознавчих вимірювань, як правило, обмежуються точковими оцінками, оскільки ряд вимірювань (вибірка) містить невелике число результатів (n ≤ 10). Розглянемо спосіб розрахунку точкових оцінок для результатів вимірювання, що найчастіше використовуються в товарознавстві продовольчих товарів. Спочатку визначається середнє арифметичне значення із сукупності значень в ряду:

статистичною оцінкою дійсного значення величини. Із збільшенням числа вимірювання середнє значення прагне до чисельного значення дійсної величини. Якщо n > 40, то Xср→ ХД. .

Для оцінки розсіяння результатів в межах ряду використовують або середню арифметичну, або середню квадратичну похибку одиничного вимірювання (у ряді рівноточних вимірювань)

Середню арифметичну похибку r розраховують, за виразом:

Хоча середня арифметична похибка дуже просто і легко розраховується, проте найбільш поширеною оцінкою розсіяння при прямих вимірюваннях є середня квадратична похибка одиничного вимірювання Sxi. Нею називають узагальнену характеристику розсіяння результатів, отриманих у ряду рівноточних вимірювань тієї самої величини внаслідок впливу випадкових похибок

Для великого ряду вимірювань при n → ∞ Sxi → σ.

Інтервальні оцінки результатів вимірювань

Інтервальною називається оцінка, що виражається у вигляді інтервалу значень, між межами якого з певною вірогідністю знаходиться істинне (або дійсне) значення вимірюваної величини. До неї відноситься довірча межа результату і довірчий інтервал.

Правило трьох сигм: якщо при багатократному вимірюванні однієї фізичної величини постійного розміру сумнівний результат окремого вимірювання відрізняється від середнього значення більш ніж на 3σ, то з вірогідністю 0,997 він є помилковим і його слід відкинути. Довірчою межею Е називається половина довірчого інтервалу:

ε = ± tpSXср.

Значення вимірюваної величини знаходиться між межами інтервалу, розрізняють верхню границю Ев=+tpSXср і нижню границю Ен=-tpSXср.

На підставі цього довірчий інтервал вимірюваної величини можна

представити у вигляді: ХД=Xср±ε=Xср±tpSXср або Xср-ε≤ХД≤Xср+ε. При точковій оцінці: Хвим = Xср ± SXср, при n = .

При інтервальному способі оцінки: Хвим = Xср ± ε, при n =, Р = .

Похибки, які впливають на точність вимірювання горизонтальних кутів теодалітами

1.Приладові похибки – виникають при виготовленні та юстуванні.

2.Похибки центрування теодоліта.

3.Похибка центрування візирних цілей (редукції).

4.Похибки власне виміряного кута (візування зорової труби та відлічування горизонтального круга).

5.Похибки за вплив зовнішніх умов.

Похибки можуть бути спричинені:

-неперпендикулярністю візирної вісі до осі обертання зорової труби (колімаційна похибка);

-нахилом обертання зорової труби (горизонтальної вісі);

-нахилом обертання теодоліта (вертикальної вісі);

-нахилом (негоризонтальністю) площини лімба;

-ексцентриситетом алідади відносно лімба;

-похибками нанесення поділок лімбу;

-реном шкалового мікроскопа.

Похибка центрування теодоліта

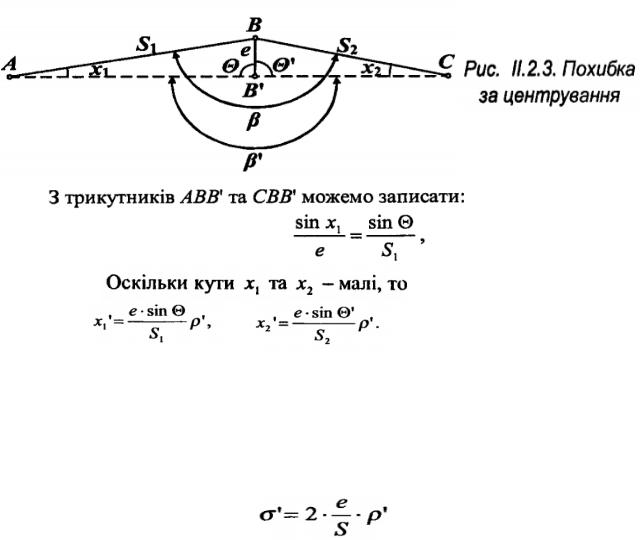
Величини е і називаються лінійним і кутовим елементами центрування відповідно. З рис. II. 2.3 очевидно, що = '-(xl + x2 ) . За однакового значення е максимальна різниця між та ' буде, коли = '=90°. Тоді, якщо рівні сторони Sl=S2=S, матимемо xl=x2=х, а похибка в кутових мінутах у куті становитиме

σ'<2х' :

Похибка за центрування теодоліта прямо пропорційна до величини е і обернено пропорційна до S. Відомо, що похибку центрування нитковим виском можна прийняти такою, що дорівнює 1 см. Якщо S=200 м, ρ'= 3437', σ=0,34' 20". За малих довжин S ця похибка буде значно більшою. При S=20м, σ 200". Для її зменшення центрують прилади оптичними центрирами.

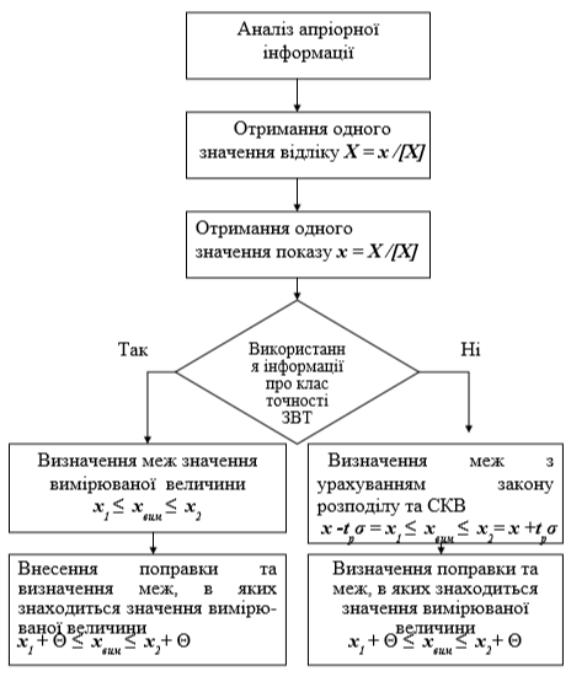
Порядок виконання операцій при однократному вимірюванні зводиться до наступних дій

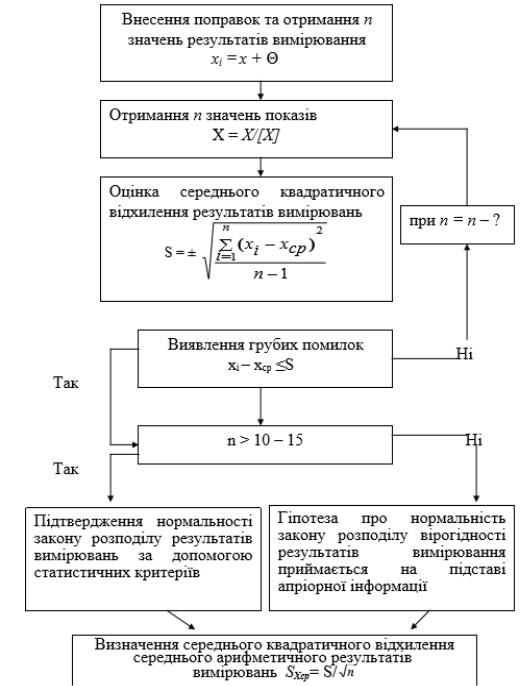
7. АЛГОРИТМИ ВИМІРЮВАННЯ ТА СПОСОБИ ПОДАННЯ ЇХ РЕЗУЛЬТАТІВ