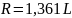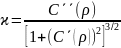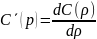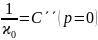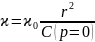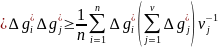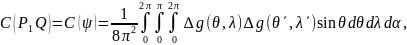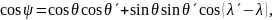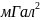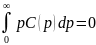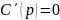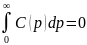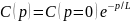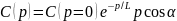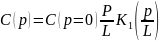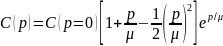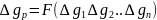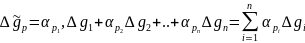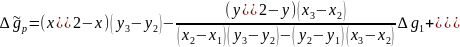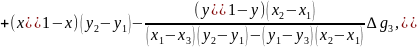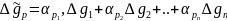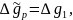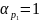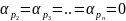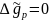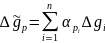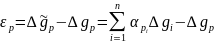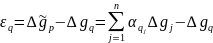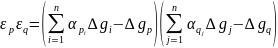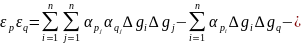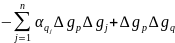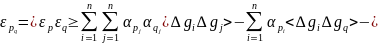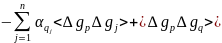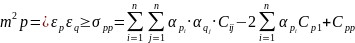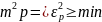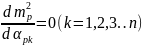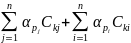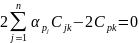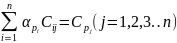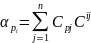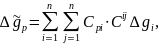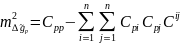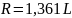
|
(8.88)
|
Параметри 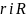 використовують лише для порівняння різних коваріацій міжсобою. Для коваріаційної функції аномалій існує нерівність:
використовують лише для порівняння різних коваріацій міжсобою. Для коваріаційної функції аномалій існує нерівність:

|
(8.89)
|
Така нерівність є справедливою і для коваріаційних функцій аномальногопотенціалу 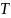 , складових відхилень прямовисних ліній
, складових відхилень прямовисних ліній 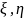 і висот квазігеоїда ζ.Кривина коваріаційної функції визначається із співвідношення:
і висот квазігеоїда ζ.Кривина коваріаційної функції визначається із співвідношення:
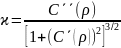
|
(8.90)
|
де:
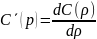

|
(8.91)
|
Радіус кривини для пункту з відомою дисперсією 
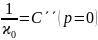
|
(8.92)
|
Параметр кривини 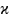 є безрозмірною величиною, який зв’язаний з кривиною
є безрозмірною величиною, який зв’язаний з кривиною 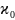 коваріаційної кривої при
коваріаційної кривої при 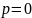 .
.
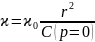
|
(8.93)
|
Для визначення величини коваріації в досліджуваному районі повинні бути заданіцентрованіаномалії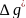 як функції координат. Для аномалії
як функції координат. Для аномалії 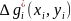 знаходять всі інші
знаходять всі інші 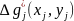 , які перебувають від неї на віддалі
, які перебувають від неї на віддалі 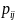 утворюють суми добутків
утворюють суми добутків 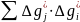 . Потім переходять до точки
. Потім переходять до точки 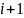 і все повторюють. Перебравши всі точки
і все повторюють. Перебравши всі точки 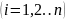 утворюють коваріації для віддалі
.
утворюють коваріації для віддалі
.
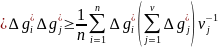
|
(8.94)
|
Так обчислення повторюють і для іншихвіддалей і в результаті знаходятьзначення коваріації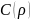 для досліджуваних віддалей. Коваріації дуже частодиференціюють або інтегрують при переході до коваріацій інших дериват гравітаційногополя, щоб вони між собою були добре узгоджені. Одержану експериментальну коваріаційну функціюапроксимують аналітичним виразом.
У залежності від застосування складають глобальну або локальну коваріаційні функції. Глобальна коваріаційна функція
для досліджуваних віддалей. Коваріації дуже частодиференціюють або інтегрують при переході до коваріацій інших дериват гравітаційногополя, щоб вони між собою були добре узгоджені. Одержану експериментальну коваріаційну функціюапроксимують аналітичним виразом.
У залежності від застосування складають глобальну або локальну коваріаційні функції. Глобальна коваріаційна функція 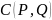 залежить тільки від сферичної віддалі
залежить тільки від сферичної віддалі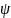 між пунктами
між пунктами 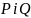 (див. рис. 42).
(див. рис. 42).
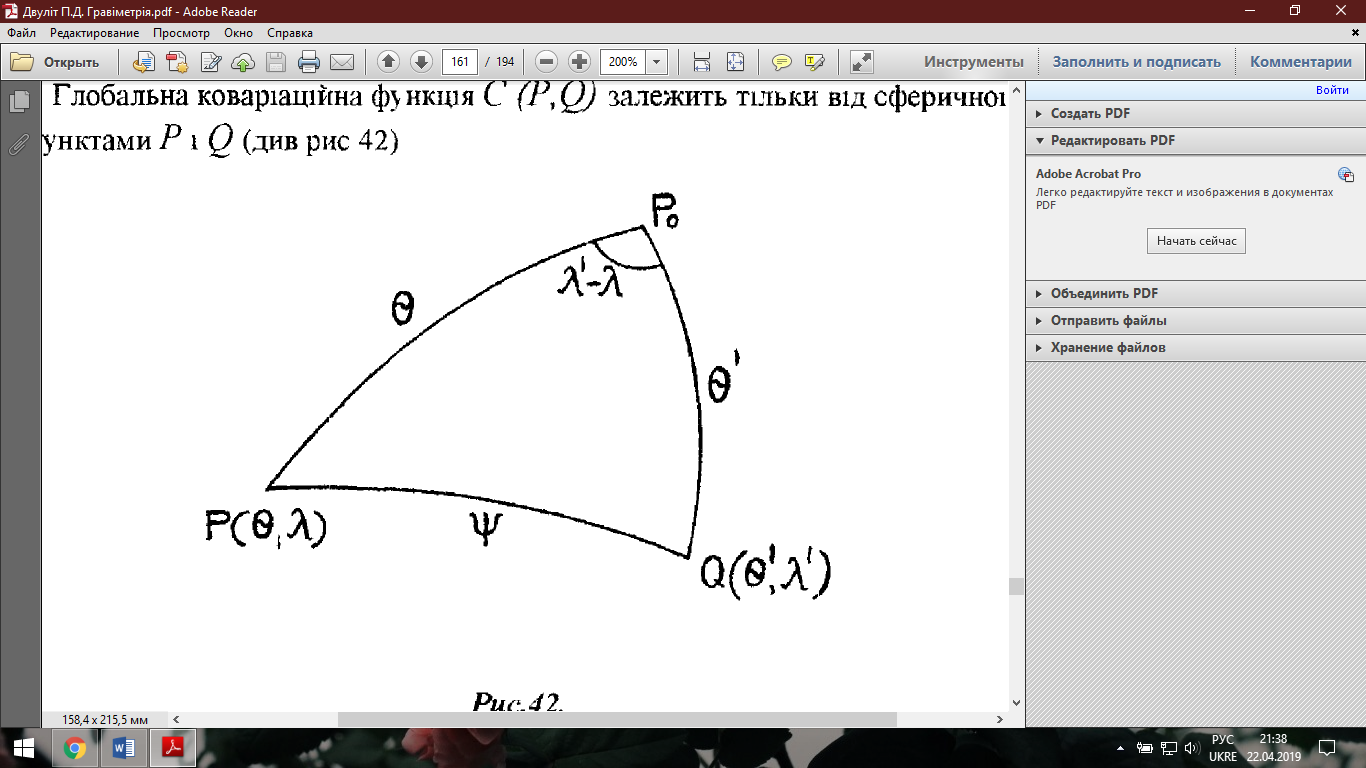 Рис.42.
Рис.42.
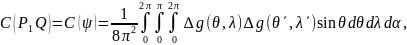
|
(8.95)
|
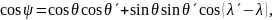
|
(8.96)
|
де:
θ, λ – сферичні координати точок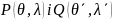 ;
;
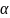 – азимут.
У таблиці 12 наведені значення глобальної коваріаційної функції аномалій Фая,яку одержав Каула в 1959 році на основі середніх даних
– азимут.
У таблиці 12 наведені значення глобальної коваріаційної функції аномалій Фая,яку одержав Каула в 1959 році на основі середніх даних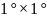 , а також значенняковаріацій із досліджень Раппа і Черніга (1974 р.) на основі гармонічних коефіцієнта
розкладу потенціалу Землі в ряд за сферичними функціями до 20 порядку.
Значення коваріаційної функції аномалій Фая
Каула і Раппа-Черніга
Таблиця 12
, а також значенняковаріацій із досліджень Раппа і Черніга (1974 р.) на основі гармонічних коефіцієнта
розкладу потенціалу Землі в ряд за сферичними функціями до 20 порядку.
Значення коваріаційної функції аномалій Фая
Каула і Раппа-Черніга
Таблиця 12
Ψ, °
|
С(ψ)
|
Каула, 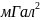
|
Раппа-Черніга,
|
0,0
0,5
1,0
1,5
2,0
2,5
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
13,0
15,0
17,0
19,0
21,0
23,0
25,0
27,0
29,0
31,0
33,0
35,0
40,0
50,0
60,0
90,0
120,0
150,0
|
+12010
+7510
+4680
+3560
+3320
+3060
+2960
+2720
+2460
+2140
+1740
+1240
+1040
+820
+760
+540
+470
+450
+340
+350
+100
+200
+180
+60
+80
+50
-80
-120
-200
-300
-40
+120
-210
|
+17950
+8020
+5730
+4530
+3760
+3210
+2800
+2220
+1820
+1530
+1310
+1130
+980
+860
+760
+590
+460
+360
+270
+200
+140
+80
+40
0
-30
-90
-130
-160
-150
-150
+20
+70
-40
|
Локальні коваріаційні функції аномалій сили ваги складають для обмеженогопростору (держава, континент, регіон). Таку поверхню можна прийняти за площину, наякій є задані аномалії.
Найважливішою умовою для коваріаційної функції є 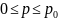 . У випадку
дослідження коваріаційної функції аналітичиий вираз повинен задовольняти умови
. У випадку
дослідження коваріаційної функції аналітичиий вираз повинен задовольняти умови
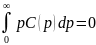
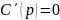
|
(8.97)
|
а для локальноїковаріаційної функції перша умова може бути слабкішою
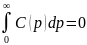
|
(8.98)
|
Найбільше застосування одержали модельніковаріаційні функції аномалії сили
ваги які наводяться нижче.
Модель експотенціалуКаула
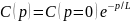
|
(8.99)
|
Модель 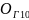 , запропонована Хірвоненом
, запропонована Хірвоненом
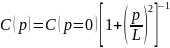
|
(8.100)
|
Модель Віскочіла
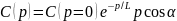
|
(8.101)
|
де:
- довжина хвилі відкорельованої аномалії.
Модель Бесселя
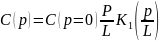
|
(8.102)
|
де:
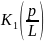 - модифікована функція Бесселя другого порядку першого степеня.
- модифікована функція Бесселя другого порядку першого степеня.
Модель Маркова другого порядку

|
(8.103)
|
Двопараметрична формула Джордана
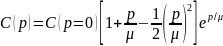
|
(8.104)
|
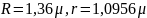 Для рівнинних районів дисперсія
Для рівнинних районів дисперсія  і відповіднорадіус кореляції
і відповіднорадіус кореляції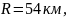 а інтервал кореляції
а інтервал кореляції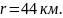 Ці аналітичні модельні функції використовують для апроксимації емпіричних
коваріаційних функцій.
8.9. Прогнозування гравіметричних аномалій
Аномалії сили ваги необхідно знати в будь-якій точці земної поверхні.Їхвикористовують для розв’язування задач гравіметрії і фізичної геодезії. Але фактичноприскорення сили ваги, яке одержують із вимірювань, визначається для обмеженої кількості пунктів. Значення величини сили ваги між цими пунктами отримують шляхомінтерполяції. Крім цього, невивченими залишаються значні території акваторій морів,океанів(більша частина Тихого океану, на півдні Атлантичного і Індійського океанів) і недостатньо вивчені території Антарктиди, Північного Льодовитого океануі Африки.
Очевидно вибір методу прогнозування (передбачення) аномалій сили ваги між пунктами спостереження є дуже важливим у задачах, які розв'язуєгравіметріяі фізичнагеодезія. Значення величин гравіметричних аномалій інтерполюють або екстраполюють. Для прогнозування аномалій в пункті
Ці аналітичні модельні функції використовують для апроксимації емпіричних
коваріаційних функцій.
8.9. Прогнозування гравіметричних аномалій
Аномалії сили ваги необхідно знати в будь-якій точці земної поверхні.Їхвикористовують для розв’язування задач гравіметрії і фізичної геодезії. Але фактичноприскорення сили ваги, яке одержують із вимірювань, визначається для обмеженої кількості пунктів. Значення величини сили ваги між цими пунктами отримують шляхомінтерполяції. Крім цього, невивченими залишаються значні території акваторій морів,океанів(більша частина Тихого океану, на півдні Атлантичного і Індійського океанів) і недостатньо вивчені території Антарктиди, Північного Льодовитого океануі Африки.
Очевидно вибір методу прогнозування (передбачення) аномалій сили ваги між пунктами спостереження є дуже важливим у задачах, які розв'язуєгравіметріяі фізичнагеодезія. Значення величин гравіметричних аномалій інтерполюють або екстраполюють. Для прогнозування аномалій в пункті 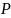 необхідно мати інформацію про функцію розкладу аномалій на даному просторі і величинами аномалій в сусідніх пунктах. Лінійну інтерполяцію використовують, коли гравіметричне знімання виконано з достатньовеликою густотою пунктів. В інших випадках використовується інформація простатистичний розклад гравіметричних аномалій або коваріаційні функції аномалій. Метою прогнозування є знаходження виразу шуканого значення аномалій в пункті
або
через функції спостережуваних аномалій
необхідно мати інформацію про функцію розкладу аномалій на даному просторі і величинами аномалій в сусідніх пунктах. Лінійну інтерполяцію використовують, коли гравіметричне знімання виконано з достатньовеликою густотою пунктів. В інших випадках використовується інформація простатистичний розклад гравіметричних аномалій або коваріаційні функції аномалій. Метою прогнозування є знаходження виразу шуканого значення аномалій в пункті
або
через функції спостережуваних аномалій 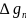 в пунктах
в пунктах 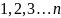 або звикористанням залежності
або звикористанням залежності
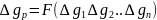
|
(8.105)
|
Якщо прогнозовану величину
позначити через  , то загальна лінійна функція
, то загальна лінійна функція 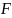 буде мати вираз
буде мати вираз
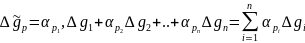
|
(8.106)
|
Коефіцієнти 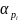 залежать тільки від взаємного положення пунктів
і пункту
. В залежності від вибору цих коефіцієнтів можна одержати різні методипрогнозування Розглянемо декілька прикладів прогнозування.
Геометрична інтерполяція. Аналітичний вираз для геометричної інтерполяції має
такий вигляд:
залежать тільки від взаємного положення пунктів
і пункту
. В залежності від вибору цих коефіцієнтів можна одержати різні методипрогнозування Розглянемо декілька прикладів прогнозування.
Геометрична інтерполяція. Аналітичний вираз для геометричної інтерполяції має
такий вигляд:
де:
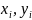 – плоскі прямокутні координати пунктів
– плоскі прямокутні координати пунктів 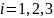 , для яких відомі величини аномалії сили ваги
, для яких відомі величини аномалії сили ваги  .
.
 – плоскі координати пункту
для якого прогнозують (інтерполюють) аномалію
– плоскі координати пункту
для якого прогнозують (інтерполюють) аномалію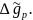 Рівняння (8.107) є рівнянням площини, яка визначена через координати трьохпунктів
Рівняння (8.107) є рівнянням площини, яка визначена через координати трьохпунктів 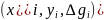 . Тут слід відзначити, що роль аплікати
. Тут слід відзначити, що роль аплікати 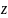 відіграє величина аномалії в пункті
відіграє величина аномалії в пункті 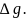 Загальний вираз для інтерпольованого значення аномалії в цьому випадку буде
Загальний вираз для інтерпольованого значення аномалії в цьому випадку буде
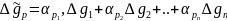
|
(8.108)
|
Представництво. У цьому методі приймають, що визначена величина аномалії в
одномупункті може бути представленою для певного оточення навколо цього пункту
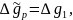
|
(8.109)
|
якщо пункт
знаходиться в околиці пункту 1, тоді коефіцієнти в загальному виразі (8.108) будуть дорівнювати
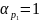
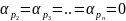
|
(8.110)
|
Нульові аномалії.Якщо на великій поверхні відсутнігравіметричні вимірювання (це передовсім поверхня океанів), то приймають
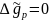
|
(8.111)
|
а всі коефіцієнти 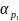 будуть дорівнювати нулю.
Жоден в представлених трьох методів прогнозування не дає максимальної точності. Щоб знайти такий метод, необхідно розв'язати загальний вираз (8.106) із застосуванням критерію мінімуму суми квадратів похибок.
Інтерполяція аномалій з найменшою дисперсією методом Г. Моріца
Інтерпольована аномалія
в будь-якій точці
представляється як лінійна функція всіх
будуть дорівнювати нулю.
Жоден в представлених трьох методів прогнозування не дає максимальної точності. Щоб знайти такий метод, необхідно розв'язати загальний вираз (8.106) із застосуванням критерію мінімуму суми квадратів похибок.
Інтерполяція аномалій з найменшою дисперсією методом Г. Моріца
Інтерпольована аномалія
в будь-якій точці
представляється як лінійна функція всіх 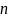 виміряних аномалій
виміряних аномалій
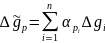
|
(8.112)
|
де:
– невідомі поки що коефіцієнти. В точці
розглянемо також істинне значення аномалії 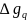 . Похибку інтерполяції можна визначити із співвідношення
. Похибку інтерполяції можна визначити із співвідношення
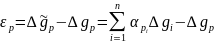
|
(8.113)
|
для похибки 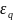 , в точці
, в точці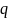 будемо мати
будемо мати
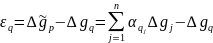
|
(8.114)
|
а добуток похибок буде
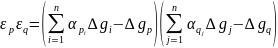
|
(8.115)
|
або:
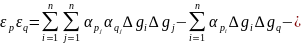
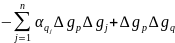
|
(8.116)
|
Добуток виміряних і інтерпольованих аномалій замінимо відповідними середніми
Величинами – коваріаціями. Тодіодержимо коваріацію похибок інтерполювання:
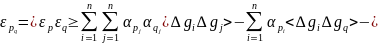
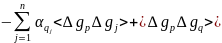
|
(8.117)
|
В виразі (8.117) фактично фігурує одна і та ж коваріація аномалій, але для різних
точок. Тобто:
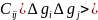 –коваріаціявиміряних аномалій
–коваріаціявиміряних аномалій
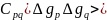 –коваріація інтерпольованих аномалій
–коваріація інтерпольованих аномалій
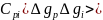 –взаємна коваріація виміряних і інтерпольованих аномалій.
Розглянемо частковий випадок формули (8.117), коли точки
–взаємна коваріація виміряних і інтерпольованих аномалій.
Розглянемо частковий випадок формули (8.117), коли точки 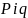 збігаються:
збігаються:
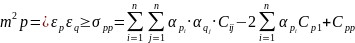
|
(8.118)
|
Ця формула визначає дисперсію інтерполювання. Крім вказаних вище коваріацій,
вона включає коефіцієнти
. Щоб їх визначити, ставимо вимогу про мінімізацію дисперсії.
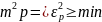
|
(8.119)
|
А це є еквівалентно системі нормальних рівнянь типу
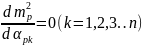
|
(8.120)
|
Похідна від першого члена формули (8.118) є сумою двох рівних членів
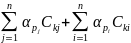
|
(8.121)
|
У розгорнутому вигляді одержимо нормальне рівняння
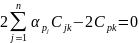
|
(8.122)
|
В цьому рівнянні немає виміряних аномалій. Після заміни індексів 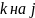 ,знаходимо систему нормальних рівнянь
,знаходимо систему нормальних рівнянь
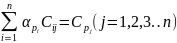
|
(8.123)
|
Значення 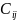 в цій системі можна розглядати як елементи симетричної матриці
в цій системі можна розглядати як елементи симетричної матриці 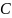 ,визначник якоїзавжди додатний. Тому матриця має обернену
,визначник якоїзавжди додатний. Тому матриця має обернену 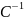 і коефіцієнти
,виражають у явному вигляді:
і коефіцієнти
,виражають у явному вигляді:
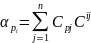
|
(8.124)
|
де:
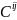 - елементи матриці
, оберненої до коваріаційної матриці
з елементами
.
Підставляючи це значення
в (8.112) і (8.118) знаходимо:
- елементи матриці
, оберненої до коваріаційної матриці
з елементами
.
Підставляючи це значення
в (8.112) і (8.118) знаходимо:
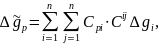
|
(8.125)
|
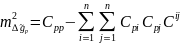
|
(8.126)
|
Отже, задача інтерполювання аномалій з найменшою дисперсією розв'язана.

використовують лише для порівняння різних коваріацій міжсобою. Для коваріаційної функції аномалій існує нерівність:
, складових відхилень прямовисних ліній
і висот квазігеоїда ζ.Кривина коваріаційної функції визначається із співвідношення:

є безрозмірною величиною, який зв’язаний з кривиною
коваріаційної кривої при
.
як функції координат. Для аномалії
знаходять всі інші
, які перебувають від неї на віддалі
утворюють суми добутків
. Потім переходять до точки
і все повторюють. Перебравши всі точки
утворюють коваріації для віддалі .
для досліджуваних віддалей. Коваріації дуже частодиференціюють або інтегрують при переході до коваріацій інших дериват гравітаційногополя, щоб вони між собою були добре узгоджені. Одержану експериментальну коваріаційну функціюапроксимують аналітичним виразом. У залежності від застосування складають глобальну або локальну коваріаційні функції. Глобальна коваріаційна функція
залежить тільки від сферичної віддалі
між пунктами
(див. рис. 42).
Рис.42.
;
– азимут. У таблиці 12 наведені значення глобальної коваріаційної функції аномалій Фая,яку одержав Каула в 1959 році на основі середніх даних
, а також значенняковаріацій із досліджень Раппа і Черніга (1974 р.) на основі гармонічних коефіцієнта розкладу потенціалу Землі в ряд за сферичними функціями до 20 порядку. Значення коваріаційної функції аномалій Фая Каула і Раппа-Черніга Таблиця 12
. У випадку дослідження коваріаційної функції аналітичиий вираз повинен задовольняти умови
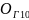 , запропонована Хірвоненом
, запропонована Хірвоненом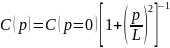
- модифікована функція Бесселя другого порядку першого степеня.
Для рівнинних районів дисперсія
і відповіднорадіус кореляції
а інтервал кореляції
Ці аналітичні модельні функції використовують для апроксимації емпіричних коваріаційних функцій. 8.9. Прогнозування гравіметричних аномалій Аномалії сили ваги необхідно знати в будь-якій точці земної поверхні.Їхвикористовують для розв’язування задач гравіметрії і фізичної геодезії. Але фактичноприскорення сили ваги, яке одержують із вимірювань, визначається для обмеженої кількості пунктів. Значення величини сили ваги між цими пунктами отримують шляхомінтерполяції. Крім цього, невивченими залишаються значні території акваторій морів,океанів(більша частина Тихого океану, на півдні Атлантичного і Індійського океанів) і недостатньо вивчені території Антарктиди, Північного Льодовитого океануі Африки. Очевидно вибір методу прогнозування (передбачення) аномалій сили ваги між пунктами спостереження є дуже важливим у задачах, які розв'язуєгравіметріяі фізичнагеодезія. Значення величин гравіметричних аномалій інтерполюють або екстраполюють. Для прогнозування аномалій в пункті
необхідно мати інформацію про функцію розкладу аномалій на даному просторі і величинами аномалій в сусідніх пунктах. Лінійну інтерполяцію використовують, коли гравіметричне знімання виконано з достатньовеликою густотою пунктів. В інших випадках використовується інформація простатистичний розклад гравіметричних аномалій або коваріаційні функції аномалій. Метою прогнозування є знаходження виразу шуканого значення аномалій в пункті або через функції спостережуваних аномалій
в пунктах
або звикористанням залежності
, то загальна лінійна функція
буде мати вираз
залежать тільки від взаємного положення пунктів і пункту . В залежності від вибору цих коефіцієнтів можна одержати різні методипрогнозування Розглянемо декілька прикладів прогнозування. Геометрична інтерполяція. Аналітичний вираз для геометричної інтерполяції має такий вигляд:
– плоскі прямокутні координати пунктів
, для яких відомі величини аномалії сили ваги
.
– плоскі координати пункту для якого прогнозують (інтерполюють) аномалію
Рівняння (8.107) є рівнянням площини, яка визначена через координати трьохпунктів
. Тут слід відзначити, що роль аплікати
відіграє величина аномалії в пункті
Загальний вираз для інтерпольованого значення аномалії в цьому випадку буде
будуть дорівнювати нулю. Жоден в представлених трьох методів прогнозування не дає максимальної точності. Щоб знайти такий метод, необхідно розв'язати загальний вираз (8.106) із застосуванням критерію мінімуму суми квадратів похибок. Інтерполяція аномалій з найменшою дисперсією методом Г. Моріца Інтерпольована аномалія в будь-якій точці представляється як лінійна функція всіх
виміряних аномалій
. Похибку інтерполяції можна визначити із співвідношення
, в точці
будемо мати
–коваріаціявиміряних аномалій
–коваріація інтерпольованих аномалій
–взаємна коваріація виміряних і інтерпольованих аномалій. Розглянемо частковий випадок формули (8.117), коли точки
збігаються:
,знаходимо систему нормальних рівнянь
в цій системі можна розглядати як елементи симетричної матриці
,визначник якоїзавжди додатний. Тому матриця має обернену
і коефіцієнти ,виражають у явному вигляді:
- елементи матриці , оберненої до коваріаційної матриці з елементами . Підставляючи це значення в (8.112) і (8.118) знаходимо: