
Алгебра
.docБ1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
Систему уравнений
вида
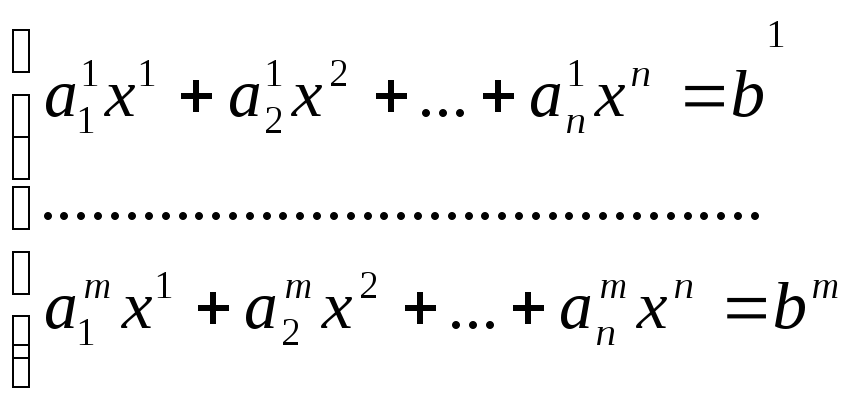
![]() (*)
(*)
будем наз-ть сист-ой
m-линейных
ур-й с n
неизвестными
![]() .
Коэф-ты этих ур-ий будем записывать в
виде матрицы
.
Коэф-ты этих ур-ий будем записывать в
виде матрицы
 ,
назыв матрицей системы.
,
назыв матрицей системы.
Числа, стоящие в
пр частях уравнений, обр-т столбец
![]() ,
наз столб своб членов.Матр сист,
дополненная спр столбцом свободны
членов, наз
расшир матрицей системы
и обозн
,
наз столб своб членов.Матр сист,
дополненная спр столбцом свободны
членов, наз
расшир матрицей системы
и обозн
![]() .Опред
матрицы – число, соотв-ее квадратичной
матрице и полученные путем ее преобр-ия
по определ правилу обозн
.Опред
матрицы – число, соотв-ее квадратичной
матрице и полученные путем ее преобр-ия
по определ правилу обозн
![]() Опред
матр, в кот вычеркнуты произвольная
строка и произвольный столбец, наз
минором. Он имеет порядок на 1 меньше,
чем исходный опред.Ранг матр - наивысший
из порядков отличных от 0 миноров этой
матрицы. Ранг неизменен при простых
преобразованиях матрицы.
Опред
матр, в кот вычеркнуты произвольная
строка и произвольный столбец, наз
минором. Он имеет порядок на 1 меньше,
чем исходный опред.Ранг матр - наивысший
из порядков отличных от 0 миноров этой
матрицы. Ранг неизменен при простых
преобразованиях матрицы.
Т.Кронекера-Капелли. Сист совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Сост СЛУ (*) однор
систему с той же матрицей коэф-ов
![]() .
По отношению к (*) она наз приведенной.
Матрица
.
По отношению к (*) она наз приведенной.
Матрица
![]() ,
сост из столбцов высоты
,
сост из столбцов высоты
![]() наз фундаментальной матрицей для
однородной системы с матрицей А, если
а)
наз фундаментальной матрицей для
однородной системы с матрицей А, если
а)
![]() ;
б)столбцы
;
б)столбцы
![]() линейно независимы; в) ранг
линейно независимы; в) ранг
![]() максимален среди рангов матрицы, удовл
усл а). столбцы
максимален среди рангов матрицы, удовл
усл а). столбцы
![]() -
ФСР.
-
ФСР.
Если
![]() -
некоторое решение системы (*), а
-
некоторое решение системы (*), а
![]() -
фундаментальная матрица ее приведенной
системы, то столбец
-
фундаментальная матрица ее приведенной
системы, то столбец
![]() (**) при любом
(**) при любом
![]() является решением (*). Наоборот, для
любого ее решения
является решением (*). Наоборот, для
любого ее решения
![]() существует такой столбец
существует такой столбец
![]() ,
что оно будет представлено (**). Выражение
,
что оно будет представлено (**). Выражение
![]() -
общее решение СЛУ
-
общее решение СЛУ
Б1 2. Линейный оператор в конечномероном пространстве, его матрица. Характеристический многочлен линейного оператора. Собственные числа и собств векторы.
Пусть
![]() и
и
![]() -
лин пр-ва с размерностями
-
лин пр-ва с размерностями
![]() и
и
![]() соотв. Будем наз опер-ом
соотв. Будем наз опер-ом
![]() ,
действующим из
,
действующим из
![]() в
в
![]() отображение вида
отображение вида![]() ,
сопоставляющее каждому элементу
,
сопоставляющее каждому элементу
![]() пространства
пространства
![]() некоторый элемент
некоторый элемент
![]() пространства
пространства
![]() .
При этом используют обозначения
.
При этом используют обозначения
![]() или
или
![]() .
.
Опер
![]() ,
действующий из
,
действующий из
![]() в
в
![]() ,
наз линейным если для любых эл-ов
,
наз линейным если для любых эл-ов
![]() ,
,
![]() и для любого компл числа
и для любого компл числа
![]() выполняется соотн:1)
выполняется соотн:1)![]() - аддитивность опер;2)
- аддитивность опер;2)![]() - однородность опер.
- однородность опер.
В мн-ве лин операторв,
действующих из
![]() в
в
![]() ,
определены операции суммы и умножения
опер-ра на скаляр.
,
определены операции суммы и умножения
опер-ра на скаляр.
Квадр матрицу
![]() с элементами
с элементами
![]() .
Это матрица наз матрицей лин опер-ра в
заданном базисе
.
Это матрица наз матрицей лин опер-ра в
заданном базисе
![]() .
.
Пусть
![]() - лин опер-р,
- лин опер-р,
![]() -
тождеств опер-р из
-
тождеств опер-р из
![]() .
Тогда мн-н относительно
.
Тогда мн-н относительно
![]()
![]() назыв характеристич мн-ом опер-ра
назыв характеристич мн-ом опер-ра
![]() .
Ур-ие
.
Ур-ие
![]() назыв характеристич ур-ем опер-ра
назыв характеристич ур-ем опер-ра
![]() .
.
Число
![]() наз собственным значением опер-ра
наз собственным значением опер-ра
![]() ,
если сущ-т некоторый ненулевой вектор
,
если сущ-т некоторый ненулевой вектор
![]() такой, что
такой, что
![]() .
При этом вектор
.
При этом вектор
![]() наз собств вектором опер-ра
наз собств вектором опер-ра
![]() ,
отвечающий собств значению
,
отвечающий собств значению
![]() .
Для того, чтобы число
.
Для того, чтобы число
![]() было собств значением опер-ра
было собств значением опер-ра
![]() н.и д., чтобы это число было корнем хар-ого
ур-ия
н.и д., чтобы это число было корнем хар-ого
ур-ия
![]() опер-ра
опер-ра
![]() .
.
Б2 3.Билинейные и квадратичные формы. Приведение их к каноническому виду. акон инерции.
Билинейной ф-ей
или бил-ой формой на лин пространстве
![]() наз ф-ия
наз ф-ия
![]() от 2-х векторов из
от 2-х векторов из
![]() ,
линейная по каждому из своих аргументов,
т.е.удовлетворяющая рав-ам:
,
линейная по каждому из своих аргументов,
т.е.удовлетворяющая рав-ам:
![]() ,
,
![]()
![]() ,
,
![]()
Квадратичной формой
или квадратичной ф-ей на лин пр-ве
![]() наз функция
наз функция
![]() ,
значение которой на любом векторе
,
значение которой на любом векторе
![]() определяется рав-ом
определяется рав-ом
![]() ,
где
,
где
![]() -
симметричная билинейная форма.
-
симметричная билинейная форма.
Паре векторов на
пл-ти сопоставим скаляр пр-ние. В силу
известных св-в скаляр-го произв это –
билинейная форма. Пусть
![]() - базис в
- базис в
![]() .
Если
.
Если
![]() и
и
![]()
![]() -
координаты векторов
-
координаты векторов
![]() и
и
![]() ,
то значение БФ
,
то значение БФ
![]() на этой паре векторов может быть вычислено
так
на этой паре векторов может быть вычислено
так
![]() или
или
![]() .
.
Здесь
![]() чисел
чисел
![]() называется ее коэффициентами в базисе.
Их запис в в квадр матрицы порядка
называется ее коэффициентами в базисе.
Их запис в в квадр матрицы порядка
![]()
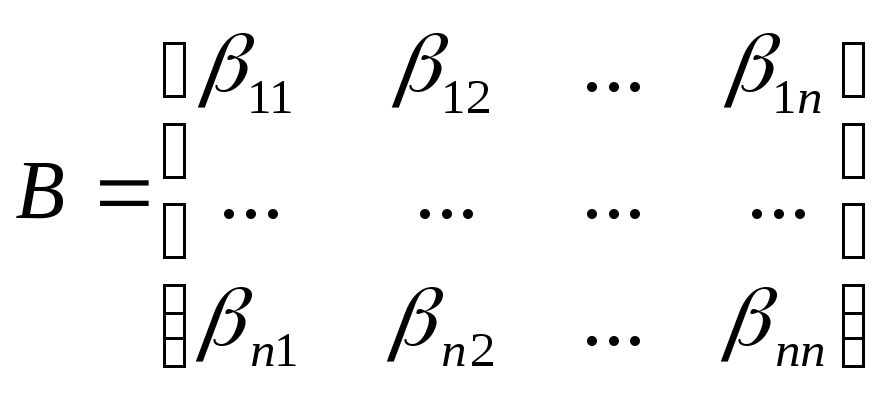 ,
,
![]() .
.
Эта матрица наз матрицей билинейной формы в данном базисе. Матрицей квадратич формы наз матрица соответ БФ.
Квадр форма
![]() ,
,
![]() ,
,
![]() ,
не имеющую попарных произведений
переменных наз квадратич формой канонич
вида. Переменные
,
не имеющую попарных произведений
переменных наз квадратич формой канонич
вида. Переменные
![]() ,
в которых квадр форма имеет канонич
вид, наз канонич переменными.
,
в которых квадр форма имеет канонич
вид, наз канонич переменными.
Один из методов преобразования квадр формы к канонич виду путем замены переменных состоит в последоват-м выделении полных квадратов. Такой м-д наз м-дом Лагранжа.
Квадр форму можно привести к канонич виду ортогонал преобразованием. При этом коэф-ты квадр формы канонич вида будут соотв знач матрицы исход квадр формы.
Закон инерции.
Теорема. Число отрицат и число положит коэф-ов в канонич виде квадр формы не завис от базиса, в котор она приведена к канонич виду.
Доказательство:
Докажем, что если
в каком-либо базисе форма
![]() приведена к канонич виду, то число
коэф-ов =-1 равно отрацат индексу формы
приведена к канонич виду, то число
коэф-ов =-1 равно отрацат индексу формы
![]() .
Пусть в базисе
.
Пусть в базисе
![]() форма
форма
![]() ранга
ранга
![]() с индексом
с индексом
![]() имеет канонич вид :
имеет канонич вид :
![]() .
.
Обозн через
![]() линейную оболочку векторов
линейную оболочку векторов
![]() ,
а через
,
а через
![]() лин оболочку остальных базисных векторов.
Для любого
лин оболочку остальных базисных векторов.
Для любого
![]() имеем:
имеем:
![]() ,
и
,
и
![]() ,
если только
,
если только
![]() .
Значит,
.
Значит,
![]() отрицательно определена на
отрицательно определена на
![]() и
и
![]() .
.
На
![]() форма
форма
![]() положит-но полуопределенная, потому
что
положит-но полуопределенная, потому
что
![]() для любого
для любого
![]() и
и
![]() .
(форма может быть =0 на ненулевом векторе,
если
.
(форма может быть =0 на ненулевом векторе,
если
![]() ).
).
![]() .
Пусть сущ-т подпр-во
.
Пусть сущ-т подпр-во
![]() размерности
размерности
![]() ,
на которм
,
на которм
![]() отриц определена. Тогда, т.к.сумма
размерностей
отриц определена. Тогда, т.к.сумма
размерностей
![]() и
и
![]() больше
больше
![]() ,
эти подпр-ва имеют ненулевой вектор
,
эти подпр-ва имеют ненулевой вектор
![]() в пересечении. Имеем
в пересечении. Имеем
![]() т.к.
т.к.
![]() и
и
![]() ,
т.к.
,
т.к.
![]() .
Получ противоречие, показывает, что
.
Получ противоречие, показывает, что
![]() .
Число коэф-ов, равных -1, равно отрицат
индексу и поэтому не зависит от базиса.
Число коэф-ов , = +1, также не зависит от
базиса, т.к.оно равно
.
Число коэф-ов, равных -1, равно отрицат
индексу и поэтому не зависит от базиса.
Число коэф-ов , = +1, также не зависит от
базиса, т.к.оно равно
![]() а ранг
а ранг
![]() и индекс
и индекс
![]() от базиса не зависят. Ч.т.д.
от базиса не зависят. Ч.т.д.
Следствие: число положит и число отрицат коэф-ов в любом диагонал виде квадр формы не зависят от базиса.
Б2 1.1 Решим систему методом Гаусса
![]()
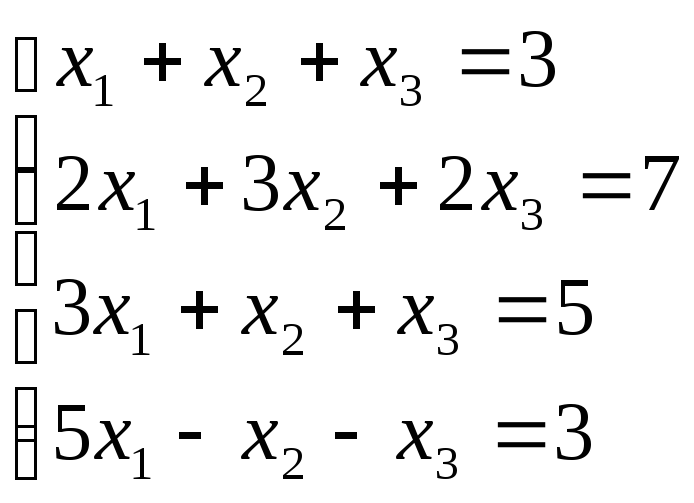
Решение.
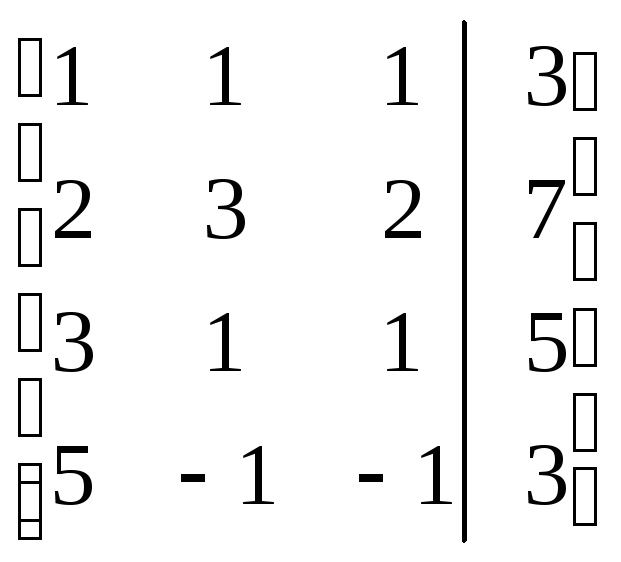 =
=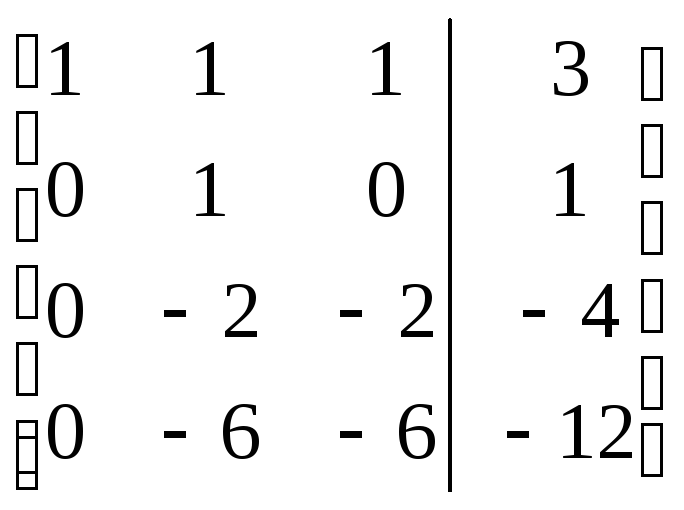 =
=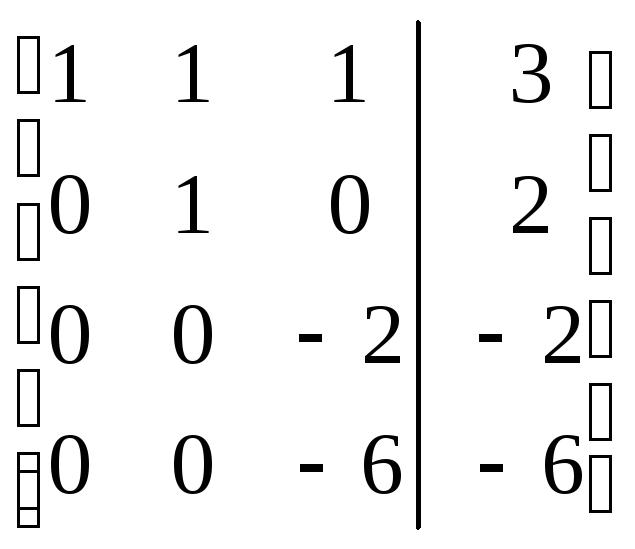 =
=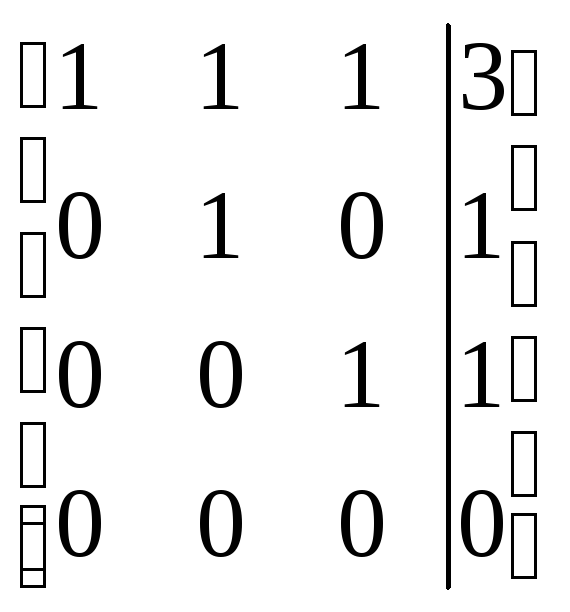 =
=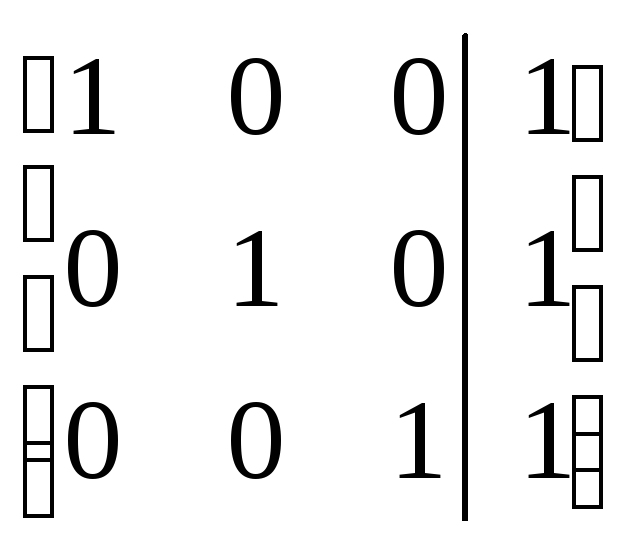
Имеем ранг матрицы
![]() -число
ненулевых строк
-число
ненулевых строк
![]() 2 ур-ия исходной системы линейно независ.
2 ур-ия исходной системы линейно независ.
Ответ:
![]()
![]() ,
,
![]()
Б2 1.2 Решить систему, пользуясь формулами Крамера.
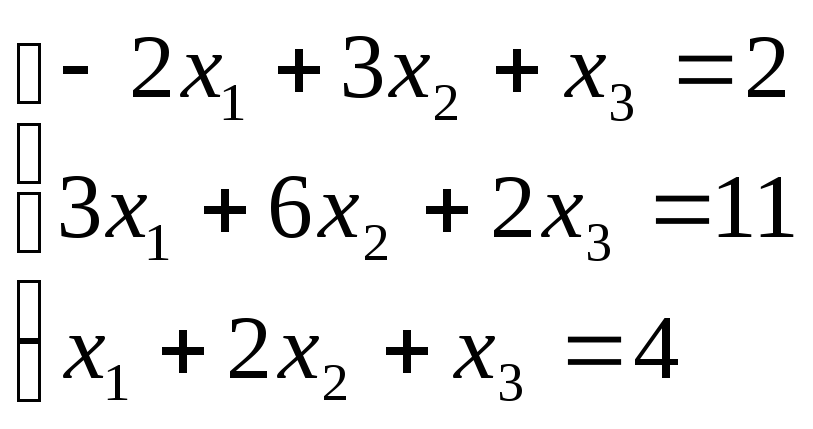
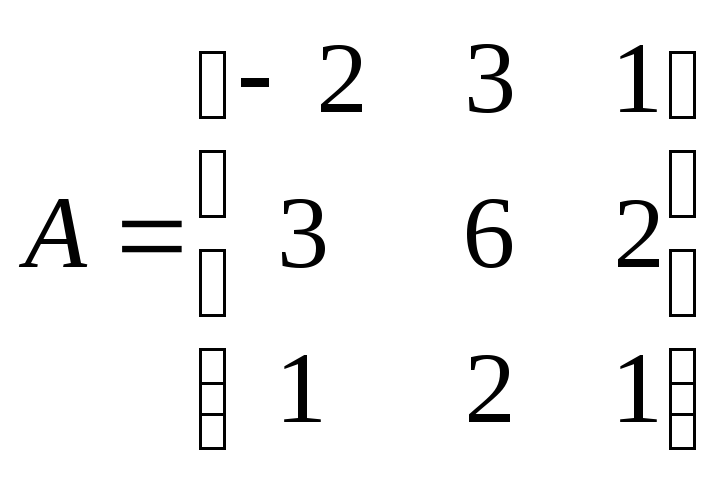
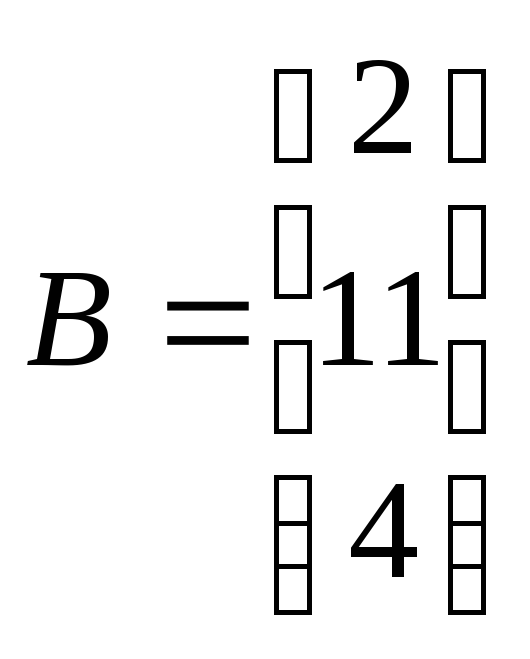
Итак,
![]() ,
,
![]() ,
,
![]()
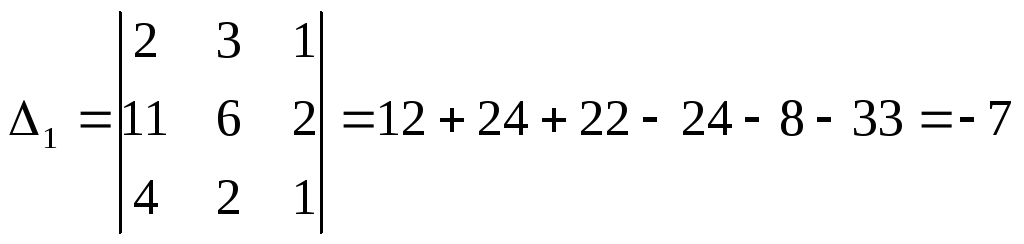

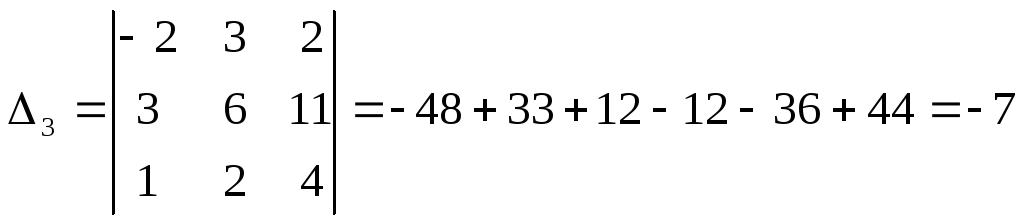
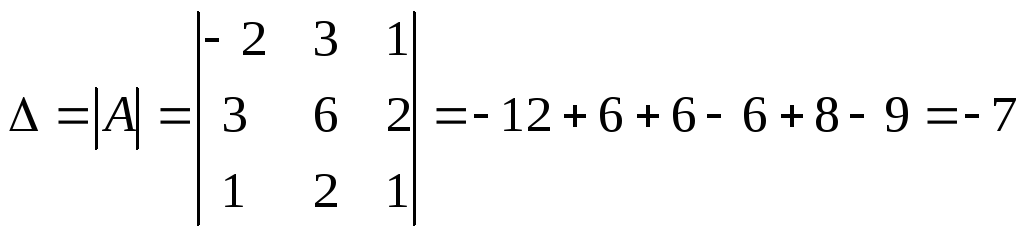
![]()
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
![]()
Б2 1.3 Решить систему лин однор ур-ий
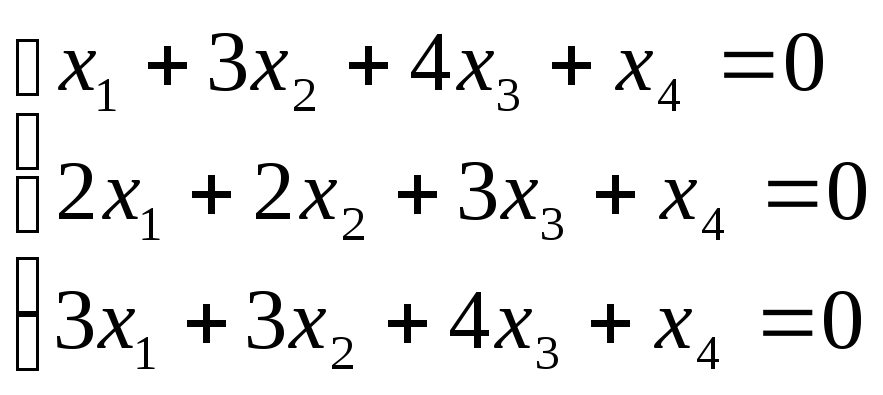
Решаем с помощью метода Гаусса
 =
= =
= =
= =
= =
= =
=

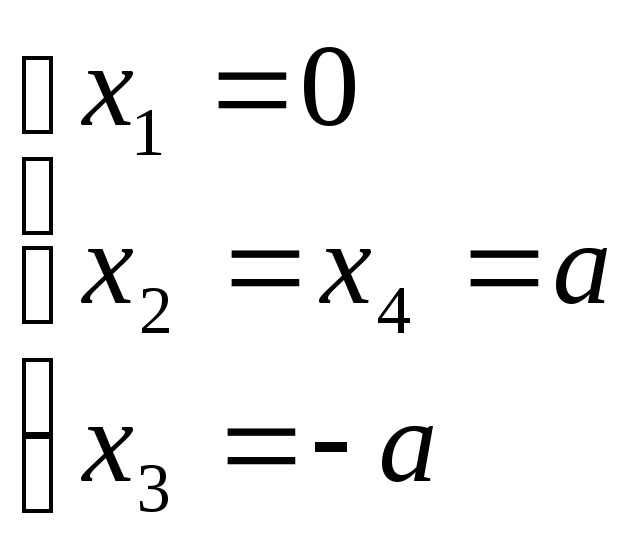
![]() -
любое действительное число
-
любое действительное число
Ответ :
![]()
Б2 2.1 Лин
преобразование
![]() лин пр-ва
лин пр-ва
![]() имеет в базисе
имеет в базисе
![]() ,
,
![]() ,
,
![]() матрицу
матрицу
 .
Найти матрицу
.
Найти матрицу
![]() того же преобраз в базисе
того же преобраз в базисе
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() -матрица
перехода от1 базиса ко 2-ому
-матрица
перехода от1 базиса ко 2-ому
![]()
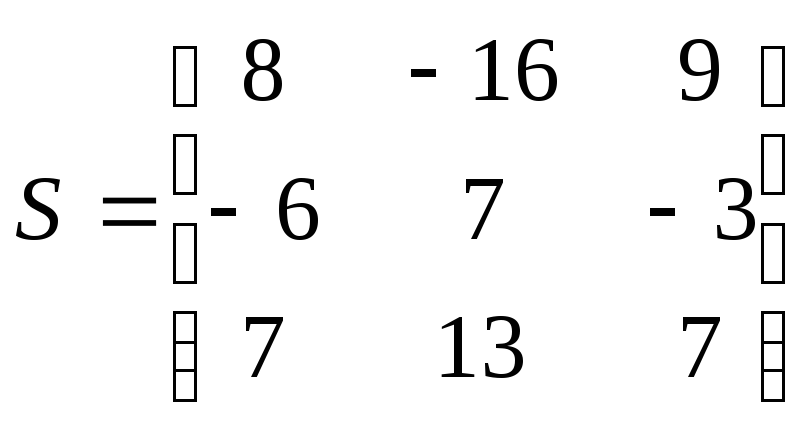 ,
,
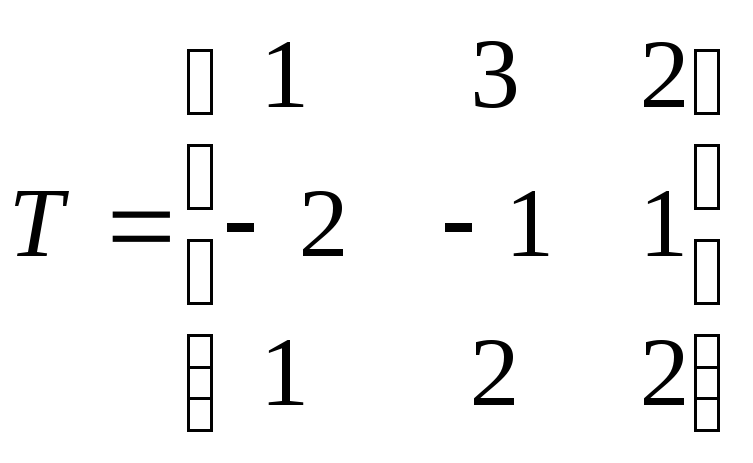
Т.к.
![]() ,
,
![]() -
базисы, то их матрицы
-
базисы, то их матрицы
![]() -невырожденные,
-невырожденные,
![]() ,
поэтому
,
поэтому
![]() ,
т.е.
,
т.е.
![]() -матрица
перехода от базиса
-матрица
перехода от базиса
![]() к базису
к базису
![]() .
Отсюда
.
Отсюда
![]()
![]() и решим ур-ие
и решим ур-ие
![]() .
.
![]() .
.
Б2 2.2 найти ядро
и дефект линейного преобразования
![]() пространства
пространства
![]() ,
если
,
если
![]() в некот базисе задано матрицей
в некот базисе задано матрицей

![]()
![]()
![]()
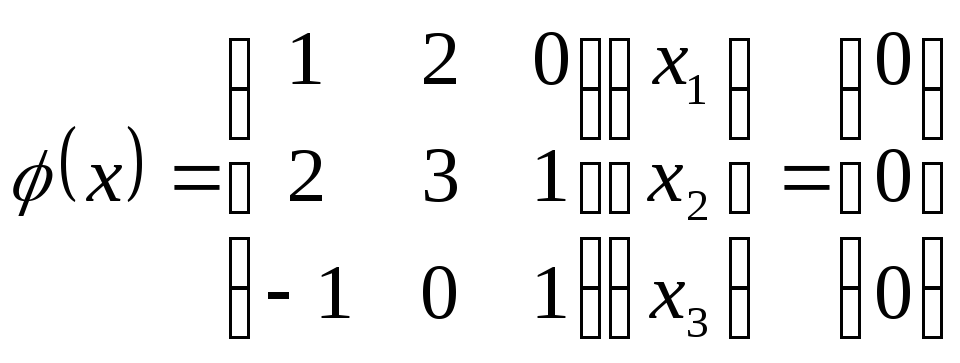
Т.е.
![]() соответствует пр-ву решений системы:
соответствует пр-ву решений системы:

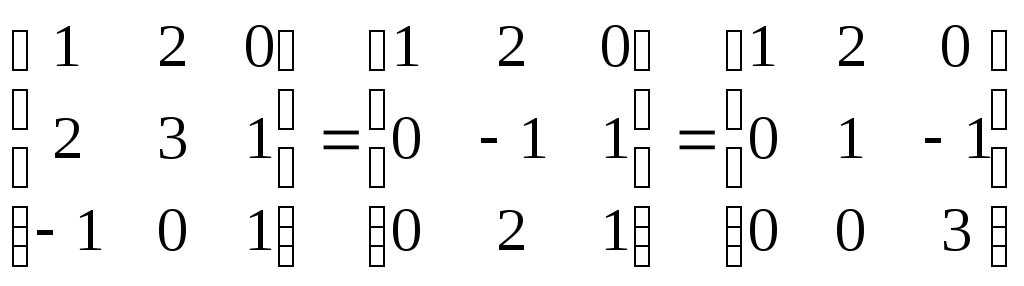 -треугол.вида
-треугол.вида
![]() ,
,
![]() ,
,
![]()
![]() система имеет
единств решение
система имеет
единств решение
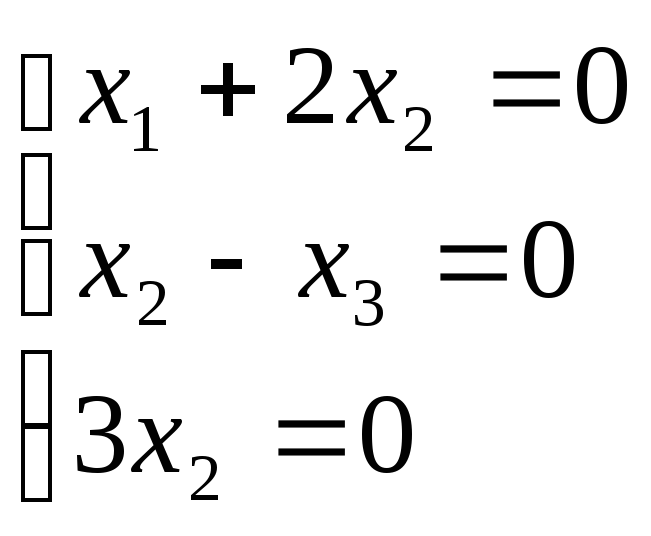
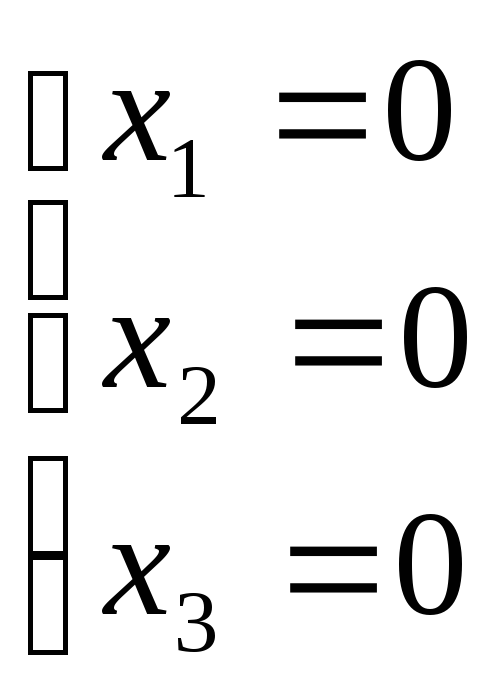
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
где
,
где
![]() -дефект
ядра
-дефект
ядра
Ответ:
![]() ,
,
![]() .
.
Б2 2.3 Найдите действительные собственные значения и собственные векторы линейного преобраования

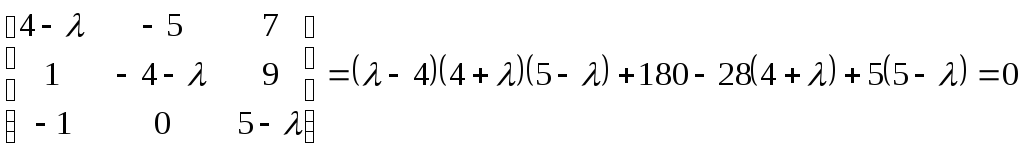
![]()
![]()
![]()
![]()
![]()
![]()
При делении столбиком
многочлена
![]() на многочлен
на многочлен
![]() получим
получим![]() .
.
(![]() )(
)(![]() )=0
)=0
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
Согласно определению комплексные числа
не яв-ся собств.значения лин.оператора.
.
Согласно определению комплексные числа
не яв-ся собств.значения лин.оператора.
![]() только
только
![]()
1)
![]()
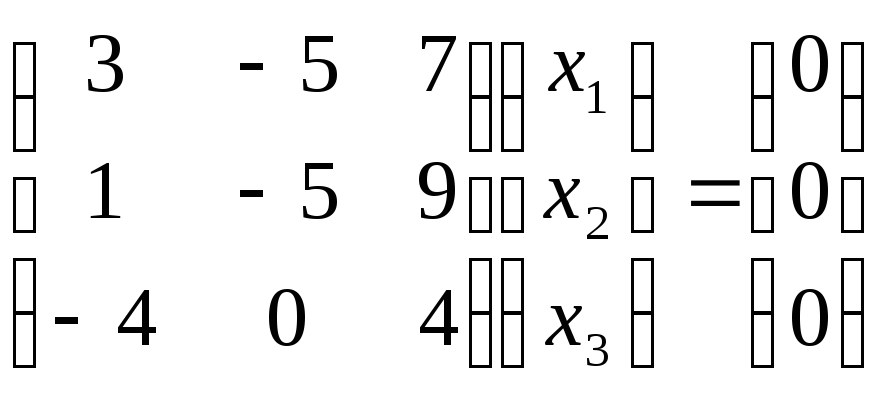
![]()
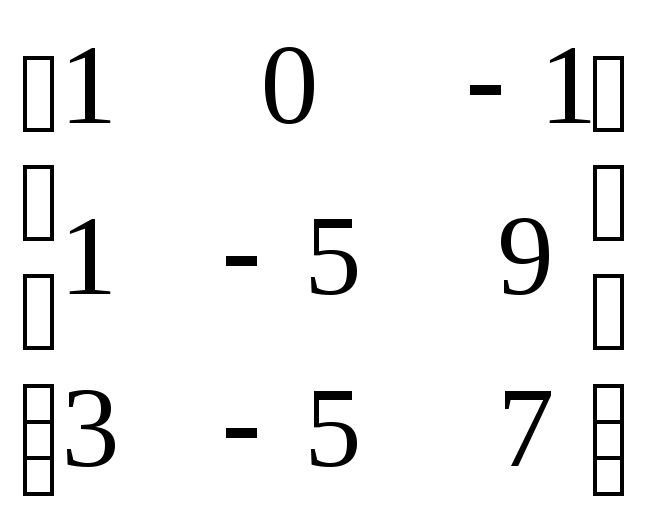 =
= =
=![]() =
=![]()
![]()
![]() ,
,
![]()
![]() ранг
ранг
![]() .
.
Поэтому размерность лин пр-ва решений = 3-2=1.
Фундаментальная
система решений содержит одно решение,
например,
 .
.
Все множество
собственных векторов лин оп-ра с
собств.значениями
![]() в корд форме имеет вид
в корд форме имеет вид
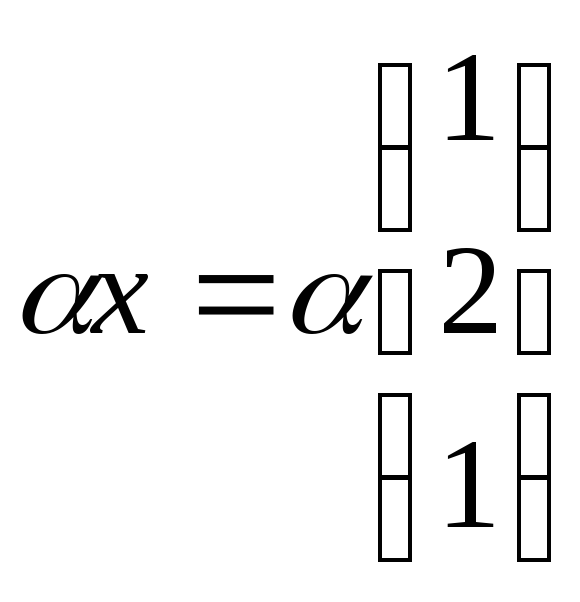 ,
где
,
где
![]() любое
число
любое
число
![]()
Ответ:
![]() ,
,
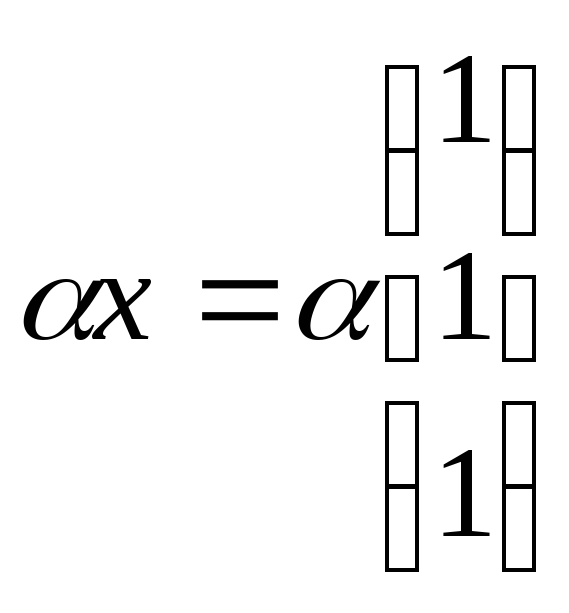 ,
,
![]() .
.
Б2 3.1 привести к каноническому виду данную бином форму
![]()
Проверим на
симметричность
![]()
![]() ,
,
![]()
![]()
![]() билинейная форма
явл симметричной
билинейная форма
явл симметричной
По определению :
квадратичная форма - численная ф-ия
![]() одного векторного аргумента
одного векторного аргумента
![]() ,
полученная из билинейной формы
,
полученная из билинейной формы
![]() при
при
![]() .
В нашем случае
.
В нашем случае
![]() ,
,
![]() .
.
Имеем
![]()
![]()
Заменим
![]() ,
,
![]()
