Выбор вида математической модели и аппроксимирующего полинома. Расчет коэффициентов полинома.
Построим график зависимости усредненного выходного параметра дальномера от устанавливаемого расстояния (рис.2).
Рис.2. График зависимости усредненного выходного параметра дальномера от устанавливаемого расстояния.
Согласно графику, можно предположить, что функциональная зависимость имеет линейный вид, т.к. диффузность данных очень мала. Функцию можно описать формулой вида , степень аппроксимирующего полинома равна единице.
Методом наименьших квадратов вычислим значения коэффициентов полинома.
Подставив полученные из опыта числовые значения и , в выбранную для аппроксимации функцию, получим систему уравнений.
Пусть система условных уравнений имеет вид:
, (2)
тогда невязка будет иметь следующий вид:
. (3)
Запишем систему нормальных уравнений:
Для упрощения записи воспользуемся обозначениями Гаусса:
В обозначениях Гаусса нормальные уравнения принимают более простой вид:
В нашем случае:
Подставив полученные значения в формулу (4), получим:
(5)
– система
имеет единственное решение.
Подставив
значения в формулу (5), сделаем вывод,
что система решена правильно, следовательно
искомая аппроксимирующая функция:
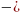именно она наилучшим
образом приближает экспериментальные
данные.
Оценим точность приближения. Для начала воспользуемся формулой (3) и найдем значение невязки:
Далее найдем оценку величин и
Оценка дисперсии условных уравнений вычисляется по формуле:
Теперь оценим погрешности полученных результатов:
Построим график , вычислим коэффициент множественной регрессии.
Согласно формуле (6), вычислим коэффициент корреляции
Рассчитаем выборочные средние:
Выборочные дисперсии:
Ковариация.
Тогда коэффициент корреляции Пирсона равен:
Связи между
признаками могут быть слабыми и сильными
(тесными). Их критерии оцениваются по
шкале Чеддока, где
– весьма высокая связь и прямая.
Найдем коэффициент множественной регрессии по формуле (7):
Подставим значение в формулу (7):
Коэффициент
множественной регрессии
– функция
аппроксимации выбрана верно.
Построим график зависимости полученных значений от аппроксимирующей функции .
Рис.3. График зависимости полученных значений от аппроксимирующей функции.
Рассчитаем доверительные границы погрешности определения коэффициентов полинома.
Воспользуемся формулами:
При том,
что
это
,
то подставив в (8)-(9) получим:
Вывод
В ходе лабораторной работы были проведены и обработаны результаты совместных измерений. Предположено и доказано, что аппроксимирующая функция подчиняется линейному закону по следующей формуле:
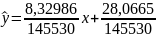
Коэффициент
множественной корреляции подтверждает
правильность данного выбора
(
).
Были построены наглядные графики,
демонстрирующие отклонение полученных
значений от значений аппроксимирующей
функции.
Вычислены погрешности аппроксимации:
Также были произведены расчёты доверительных интервалов для истинных значений измеряемых величин на основе распределения Стьюдента: