Министерство образования и науки российской федерации Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «миэт»

Институт «Микроприборов и систем управления» (МПСУ)

Лабораторная работа №5 по дисциплине

«Метрология и электрорадиоизмерения» Тема: «Обработка результатов совместных измерений»

Цель работы: ознакомление с методикой обработки результатов совместных измерений, получение градуировочной характеристики дальномера и оценка погрешностей совместных измерений.

Продолжительность работы: 4 часа.

Аппаратура: персональный компьютер, дальномер HC-SR04, рулетка, генератор сигналов специальной формы NI PXI-5402, цифровой осциллограф TDS-1000B; рабочая станция NI ELVIS.

Выполнили студенты группы «ИВТ-34»: Никитина София Геннадьевна

Чемякина Юлия Евгеньевна

Преподаватель: Калеев Дмитрий Вячеславович

2021 г.

Содержание

1. Теоретические сведения 3

2. Выполнение работы 11

2.1. Подготовка измерительного эксперимента и сбор данных. 11

2.2. Сбор измерительной информации. 12

2.3. Выбор вида математической модели и аппроксимирующего полинома. Расчет коэффициентов полинома. 13

3. Вывод 21

1. Теоретические сведения

Градуировочная характеристика средства измерений - зависимость между значениями величин на выходе и входе средства измерений, составленная в виде таблицы, графика или формулы.

Совместные измерения - проводимые одновременно измерения двух или нескольких разноименных величин для определения зависимости между ними.

Совместные и совокупные измерения обычно выполняют так, что получаемое число уравнений, связывающих измеряемые величины, превышает число последних. При этом из-за погрешностей измерений нельзя найти такие значения неизвестных, при которых все уравнения выполнялись бы. В этих условиях значения неизвестных, принимаемые за их оценки, находят проводя регрессионный анализ, методом наименьших квадратов.

При этом выполняют следующие шаги:

• Постановка измерительного эксперимента, сбор данных.

• Выбор вида математической модели.

• Подбор аппроксимирующей функции.

• Расчет по экспериментальным данным параметров выбранной аппроксимирующей функции.

Выбор вида математической модели. Задача выбора вида функциональной зависимости - задача не формализуемая, так как одна и та же кривая на данном участке примерно с одинаковой точностью может быть описана самыми различными аналитическими выражениями. Так, например, U-образная кривая может быть описана участком параболы, гиперболы, эллипса или синусоиды. Рациональный выбор того или иного аналитического описания может быть обоснован лишь при учете определенного перечня требований. Главное требование к математической модели — это удобство ее последующего использования. Основной помехой для установления вида исследуемой зависимости является случайный разброс экспериментальных данных.

Если случайный разброс координат 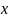и почти отсутствует или, как иногда говорят, диффузность исходных данных очень мала, то привлечение статистических методов для их обработки излишне и кривую можно просто провести через эти точки (рис 1.а).

Рис. 1.

Если диффузность исходных данных значительна, т.е. вследствие случайного разброса отсчетов и точки на графике имеют существенный случайный разброс, то соединение их между собой отрезками прямых линий (рис. 1 б) просто бессмысленно и для обработки таких данных надо применять простейшие или более сложные статистические методы.

Одним из таких простейших экспресс-методов статистической обработки является метод обведения контура плавных границ полосы рассеяния экспериментальных точек. Если при этом для сохранения плавности этих границ какие-то из точек приходится оставить вне контура (рис. 1 в), то их следует рассматривать как возможные промахи или аномально большие случайные отклонения. Форма обведенной контуром полосы рассеяния экспериментальных точек чаще всего уже позволяет вынести суждение о характере функциональной зависимости

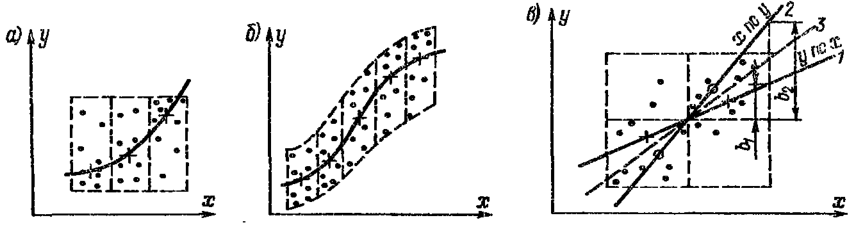
Рис. 2.

При очень большой диффузности экспериментальных данных, когда использование метода контура не дает ответа, может оказаться полезным метод медианных центров. Сущность этого метода поясняется рис. 2. Обведенное контуром поле точек делят на несколько частей, и в каждой из них находят медианный центр, т.е. пересечение вертикали и горизонтали слева и справа, и выше и ниже которых оказывается равное число точек. Затем через эти медианные центры проводят плавную кривую. Так как общее число отсчетов, как правило, не очень велико, то не следует стремиться к разделению поля точек на излишне большое число областей. Положение и форма кривых на рис. 2 а и б определяется соответственно тремя и пятью точками. Поэтому и поля точек должны быть разбиты не более чем на три и пять областей.

Подбор аппроксимирующей функции.

После того как каким-либо из описанных выше методов установлен графических вид искомой функциональной зависимости, задача состоит в выборе ее аналитического описания, т.е. в подборе аппроксимирующей функции.

Известно, что любую функцию для однофакторных совместных измерений можно описать многочленом 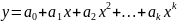, она же линейная регрессия. В простейшем случае может использоваться модель вида . В случае линейной регрессии для определения параметров модели используется метод наименьших квадратов.

Также очень удобными при аппроксимации оказываются дробно-рациональные функции. Их практическая особенность состоит в том, что чаще всего исследователь не подозревает и не может догадаться, что интересующая его зависимость аппроксимируется именно этими функциями. Мы легко узнаем только простейшую равнобокую гиперболу, асимптотами которой служат оси координат. Но если эта гипербола сдвинута или перевернута, то мы уже ее не узнаем, а попытка аппроксимировать ее многочленом приводит к громоздкому выражению. Поэтому целесообразно взять себе за правило, прежде чем использовать аппроксимацию многочленом или экспонентами, обязательно проверить, не является ли искомая кривая простейшей, сдвинутой от начала координат гиперболой.

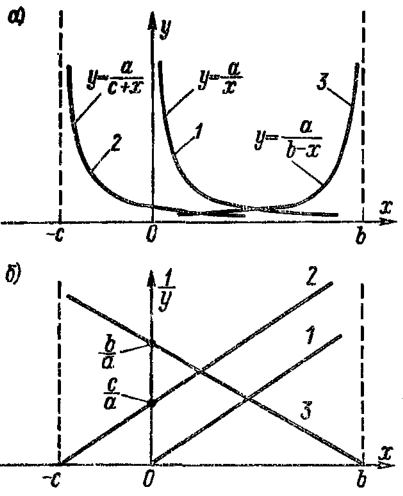
Рис. 3.

Проверка того, является ли данная кривая гиперболой, состоит в построении графика (рис 3). Если является, то экспериментальные точки примерно (из-за наличия погрешностей) ложатся на прямую.

При этом замена координаты y на допустима лишь в том случае, если сдвиг по этой координате отсутствует, т.е. другая ось является асимптотой такой гиперболы. Это вызвано тем, что при сдвиге, например, вдоль оси x аналитическое описание гиперболы имеет вид 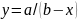. Обращение оси y приводит к зависимости вида , т.е. прямой в координатах 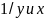. 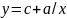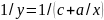При сдвиге же вдоль оси y уравнение гиперболы имеет вид , а следовательно, не есть прямая линия.

Для того чтобы использовать МНК для дробно-рациональной модели необходимо произвести замену , если это возможно, и оценивать параметры упрощенной модели.

Расчет по экспериментальным данным параметров выбранной аппроксимирующей функции.

Подставив полученные из опыта числовые значения 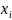и , в выбранную для аппроксимации функцию, получим ряд уравнений.

(1)

Как уже отмечалось, обычно число уравнений системы (1) превышает число неизвестных и из-за погрешностей измерений нельзя найти такие значения измеряемых величин, чтобы одновременно удовлетворились все уравнения, даже если они сами по себе точно известны. Поэтому уравнения (1) в отличие от обычных математических уравнений принято называть условными. При подстановке в условные уравнения (1) найденных каким-то путем значений неизвестных по отмеченным причинам получим

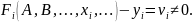
Величины 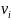принято называть невязками. Всеобщее признание получило такое решение условных уравнений, которое приводит к минимуму сумму квадратов невязок, что осуществляется методом наименьших квадратов. Теоретически показано, что при нормальном распределении погрешностей метод наименьших квадратов приводит к оценкам неизвестных, удовлетворяющих принципу максимума правдоподобия, т.е. наиболее вероятным оценкам.

Пусть система условных уравнений имеет вид

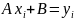, (2)

причем A и B - искомые неизвестные, и - результаты i-го наблюдения величин и .

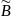Если в (2) подставить какие-то оценки величин и , то получим невязки:

.

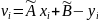Найдем оценки величин и исходя из следующий условий МНК:

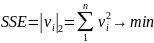
SSE - сумма квадратов невязок (Sum of Squared Errors).

Для выполнения этого условия необходимо, чтобы

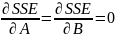
Найдем эти частные производные и приравняем их нулю:

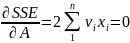
Отсюда получаем систему так называемых нормальных уравнений:

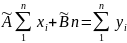
При написании нормальных уравнений часто пользуются обозначениями Гаусса:

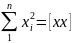
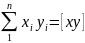
и т.д.

В обозначениях Гаусса нормальные уравнения принимают более простой вид:

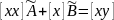
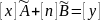(3)

Нужно обратить внимание на две важные особенности матрицы коэффициентов при неизвестных в системе уравнений (3):

1. Матрица этих коэффициентов симметрична относительно главной диагонали.

2. Все элементы главной диагонали положительны.

Эти свойства являются общими, они не зависят от числа неизвестных, но в данном примере показаны применительно к случаю с двумя неизвестными.

Число нормальных уравнений равно числу неизвестных, и их решение известными методами дает интересующие нас оценки измеряемых величин. Наиболее кратко решение записывается с помощью определителей:

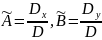, (4)

где

.

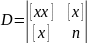Определител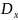и и получают из главного определителя системы D путем замены столбца с коэффициентами при неизвестных и на столбец со свободными членами:

,

.

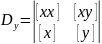Теперь нужно оценить погрешности полученных результатов. В упрощенном виде оценки дисперсий найденных значений неизвестных можно вычислить, пользуясь формулами:

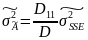
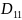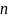где и - алгебраические дополнения элементов и определителя D соответственно (они получаются путем удаления из матрицы определителя D столбца и строчки, на пересечении которых находится данный элемент). 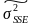- оценка дисперсии условных уравнений.

Оценка дисперсии условных уравнений вычисляется по формуле:

Метод наименьших квадратов дает возможность найти оценки измеряемых величин и оценить их средние квадратические отклонения.

Доверительные интервалы для действительных значений измеряемых величин строят на основе распределения Стьюдента. Число степеней свободы в общем случае равно 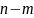. В нашем случае m = 2 - число оцениваемых параметров.

Оценка рассеяния экспериментальных данных значением коэффициента корреляции. Коэффициент корреляции есть показатель тесноты группирования экспериментальных данных относительно принятой модели. На практике часто применяет коэффициент корреляции Пирсона, который характеризует существование линейной зависимости между двумя величинами X и Y, и определяется следующей формулой:

Однако коэффициент корреляции 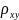значений и применительно к однофакторной зависимости характеризует тесноту группирования данных лишь относительно некоторой прямой. При более сложной зависимости (рис. 4) коэффициент корреляции будет оценивать тесноту экспериментальных точек относительно некоторой прямой, обозначенной буквой А, что, естественно, несет мало сведений о тесноте их группирования относительно искомой кривой 1-2-3.

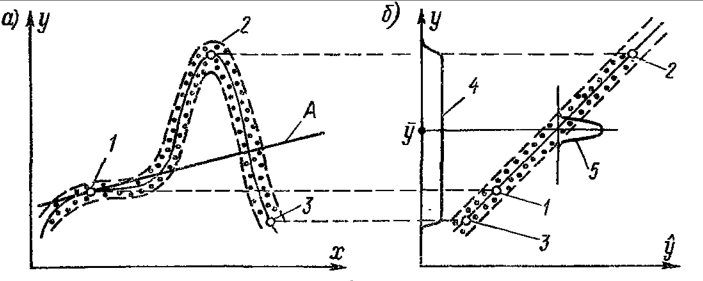
Рис. 4.

Однако существует понятие коэффициента множественной корреляции, расчетная оценка которого правомерна для любых многофакторных зависимостей, в том числе и для сложных нелинейных однофакторных зависимостей.

Если используемая в качестве модели функция 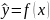есть однозначная функция x, т.е. любому заданному x соответствует лишь одно определенное значение 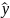, то при отсутствии погрешностей экспериментальных данных тождество изобразится в координатах 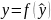(рис. 4 б) в виде биссектрисы прямого угла, как бы ни была сложна используемая модель. Если же погрешность экспериментальных данных не равна нулю, т.е. экспериментальные точки на рис. 4-а располагаются не на кривой 1-2-3, а в некоторой полосе вдоль этой кривой, то на рис. 4-б экспериментальные значения расположатся в некоторой полосе вокруг прямой . Это обусловлено тем, что каждому значению x соответствует (при однозначной модели) лишь одно значение , а экспериментальные значения при заданном x могут быть как больше , так и меньше.

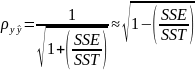
где 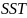- сумма квадратов модели (Sum of Squares Total) регрессии, которая определяется следующим образом:

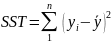
Принято считать, что если коэффициент множественной регрессии 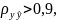то функция аппроксимации выбрана верно.