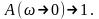Фигуры Лиссажу

Фигуры Лиссажу - замкнутые траектории, прочерчиваемые точкой, совершающей одновременно гармонические колебания в двух взаимно перпендикулярных направлениях.

Рис.4. Вид фигур Лиссажу при отношении частот сигналов 3:1; 1, 2 - точки пересечения с вертикальной секущей; 3, 4 - точки пересечения с горизонтальной секущей

Рис.3. Вид фигур Лиссажу при равенстве частот сигналов; 1, 2 - точки пересечения с вертикальной секущей; 3, 4 - точки пересечения с горизонтальной секущей

Вид фигур Лиссажу зависит от соотношения между амплитудами, частотами и фазами обоих колебаний. В случае равенства частот колебаний фигура Лиссажу представляет собой эллипс (рис.3), который при разности фаз 0 или π вырождается в отрезок прямой, а при разности фаз π/2 и равенстве амплитуд превращается в окружность. Если частоты колебаний не равны, разность фаз изменяется во времени, что приводит к образованию фигур Лиссажу сложной формы как устойчивых, так и динамически изменяющихся во времени.

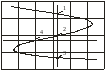
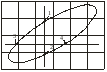
Если частоты колебаний относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов колебаний, движущаяся точка возвращается в исходное положение, образуя устойчивую фигуру Лиссажу (рис.4).

Математический анализ показывает, что для соотношения частот колебаний справедливо следующее выражение:

,

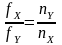где 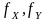- частоты гармонических колебаний вдоль осей X и Y соответственно; 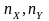- количество точек пересечения горизонтальной и вертикальной секущих с неподвижной фигурой Лиссажу.

Горизонтальная и вертикальная секущие проводятся таким образом, чтобы каждая секущая имела максимальное число точек пересечений с фигурой Лиссажу (см. рис.3 и 4).

Фигуры Лиссажу можно наблюдать на экране осциллографа в режиме развертки XY; Наблюдение фигур Лиссажу - удобный метод исследования соотношений между амплитудами, частотами и фазами гармонических колебаний.

Рассмотрим способ определения соотношения между амплитудами и фазами двух гармонических сигналов на примере апериодического звена.

Апериодическое звено первого порядка описывается дифференциальным уравнением

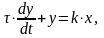
где 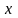- входной гармонический сигнал; 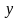- выходной гармонический сигнал; 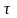- постоянная времени, определяющая частотные свойства звена; 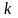- коэффициент передачи звена.

Примером апериодического звена является RC-цепь (рис.5).

Рис.5. Апериодическое звено (RC-цепь)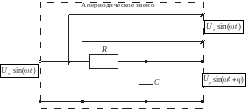

Дифференциальное уравнение RC-цепи:

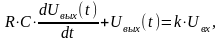
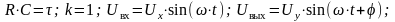
где 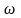- частота сигнала.

Для определения амплитудно-частотной (АЧХ) и фазо-частотной характеристик (ФЧХ) звена найдем его комплексную передаточную характеристику, которая определяется уравнением

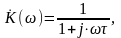
где 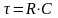для RC-цепи, - частота сигнала.

Амплитудно-частотная характеристика апериодического звена определяется уравнением

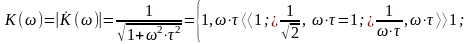
Фазо-частотная характеристика апериодического звена определяется следующим уравнением:

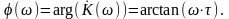
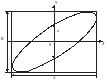
Рис.6. Фигура Лиссажу

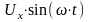Для определения отношения амплитуд и разности фаз гармонических сигналов на входе и выходе апериодического звена (АЧХ и ФЧХ апериодического звена) методом фигур Лиссажу с помощью осциллографа необходимо на вход CH1 осциллографа подать сигнал, поступающий на вход звена , а на вход CH2 осциллографа подать сигнал с выхода звена 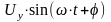. На экране осциллографа появится изображение фигуры Лиссажу (рис.6).

При этом:

• максимальный размер изображения сигнала по оси : ;

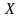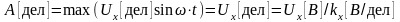• максимальный размер изображения сигнала по оси : ;

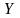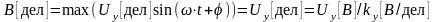• размер изображения сигнала по оси в момент времени, когда значение сигнала по оси равно нулю:

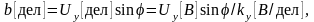
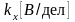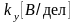где - коэффициент развертки осциллографа по оси , - коэффициент развертки осциллографа по оси .

Тогда ФЧХ звена определяется уравнением

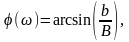
а АЧХ звена

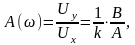
где 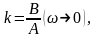так как для апериодического звена