Билет № 9
Высотная линия положения, ее уравнение. Свойства высотных ЛП.
Высотная линия положения, ее уравнение. Линией положения называется кассательная (или хорда), проведенная к изолинии вблизи счислимого места и замещающая собой изолинию. Уравнение изолинии имеет следующий вид
![]()
![]() cos
cos
![]() +
+![]() wsin
wsin![]() =
n,
=
n,
![]() -
направление градиента,
n = (Uo
- Uc)/g
- перенос,
g - модуль градиента
навигационного параметра,
Uo
- обсервованный параметр (измеренный
навигационный параметр, исправленный
всеми поправкам);
Uc
- счислимый параметр, т.е. рассчитанный
по формуле для заданных счислимых
координат.
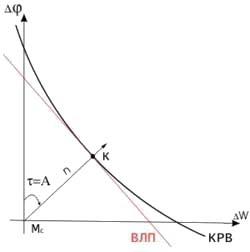
Кассательная к кругу равных
высот является высотная
линия положения - ВЛП.
Получим её уравнение.
-
направление градиента,
n = (Uo
- Uc)/g
- перенос,
g - модуль градиента
навигационного параметра,
Uo
- обсервованный параметр (измеренный
навигационный параметр, исправленный
всеми поправкам);
Uc
- счислимый параметр, т.е. рассчитанный
по формуле для заданных счислимых
координат.
Кассательная к кругу равных
высот является высотная
линия положения - ВЛП.
Получим её уравнение.
Из МОСа известно, что модуль и направление градиента можно вычислить через частные производные:
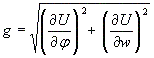
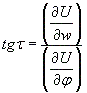
При ОМС в мореходной астрономии в качестве навигационного парметра служит высота. По основным дифференциальным формулам мореходной астрономии имеем:
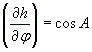 и
и
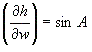 Следовательно,
Следовательно,![]() Откуда,
Откуда,![]() =
А.
=
А.
Уравнение ВЛП имеет следующий вид:
![]() cosА
+
cosА
+
![]() wsinА
= n = ho
- hc
wsinА
= n = ho
- hc
Свойства высотных линий.
1). ВЛП - это приближенная линия. Из рисунка видно, что чем меньше измеряемая высота, тем больше радиус круга равных высот и тем на большем участке ВЛП совпадает с КРВ. Чем больше высота, тем меньше радиус изолинии, следовательно, на меньшем участке происходит совпадение изолинии и ВЛП. Для того чтобы ошибка обсервации была бы минимальной от замены изолинии ВЛП при ОМС высоты светил не должны превышать 50° - 60° и в этом случаи ошибки от замены изолиний ВЛП не будет. Чтобы не было соблазна считать большие счислимые высот в таблицах ВАС-58 по таблице 1 невозможно рассчитать поправки для высот более 73°.

По этой причине методу ВЛП присуще методическая погрешность. Построив две ВЛП, получим обсервованную точку Мо, точку пересечения 2-х ВЛП. Но на самом деле судно находится в точке пересечения изолиний в М1. Методическая погрешность будет тем больше, чем больше высоты светил и чем больше переносы. Чтобы свести к минимуму методическую погрешность, необходимо определяться по светилам с небольшими высотами, а если это невозможно, то применять метод последовательных приближений (метод иттераций). Получив на первом этапе обсервованную точку Мо, принимаем её за счислимую, и повторяем сначала процесс вычислений. Обычно на 2-ом или 3-ьем шаге вычислений получается обсервованная точка, практически совпадающая с точкой пересечения по изолиниям. Естественно, что процесс последовательных приближений выполняется не вручную, а на компьютере по специально разработанной программе, в основе которой лежит аналитическим метод. Этот метод будет рассмотрен ниже

2). Градиент ВЛП равен 1. Вспомним ещё одно определение градиента
![]()
где
![]() U
- изменение навигационного параметра,
U
- изменение навигационного параметра,![]() n
- смещение линии положения вследствии
изменения навигационного параметра на
величину
n
- смещение линии положения вследствии
изменения навигационного параметра на
величину![]() U.
Т.к.
градиент равен единице, то любая
погрешность в высоте
U.
Т.к.
градиент равен единице, то любая
погрешность в высоте![]() h
вызывает смещение ВЛП параллельно самой
себе на величину
h
вызывает смещение ВЛП параллельно самой
себе на величину![]() n
=
n
=![]() h.
h.
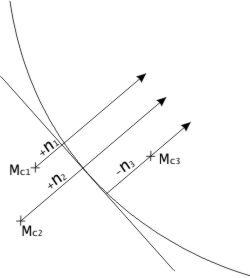
3).
Положение ВЛП на карте не зависит от
принятых счислимых координат.
(Это
самое важное свойство ВЛП). Из предыдущего
параграфа мы знаем, что положение КРВ
определяется только обсервованной
высотой ho
и координатами полюса освещения.
Следовательно, в определенный момент
времени для заданного светила с измеренной
высотой ho
положение КРВ остается неизменным. Т.к.
ВЛП это кассательная к кругу равных
высот, то и положение ВЛП остается
неизменным. Это означает, что при
вычислении элементов ВЛП для различных
счислимых точек Мс1,
Мс2
и Мс3,
но для одних и тех же значений величин
ho,
tгр
и
![]() ,
получим разные значения переносов ni
= ho
- hci.
Однако в результате прокладки из всех
счислимых точек будет получена одна и
та же ВЛП.
Это свойство позволяет
производить ОМС в независимости от
точности счисления. На этом свойстве
основан метод перемещенного места,
который является составной частью
ускоренных способов астрономических
обсерваций.
,
получим разные значения переносов ni
= ho
- hci.
Однако в результате прокладки из всех
счислимых точек будет получена одна и
та же ВЛП.
Это свойство позволяет
производить ОМС в независимости от
точности счисления. На этом свойстве
основан метод перемещенного места,
который является составной частью
ускоренных способов астрономических
обсерваций.