4.2Статические и динамические характеристики средств измерений

Характеристики средств измерения

В режиме статического преобразования измеряемой величины

В режиме динамического преобразования измеряемой величины

Рис. 4.4 Статические и динамические характеристики средств измерений.

Как уже отмечалось выше, измерения делятся на статические и динамические. Рассмотрим метрологические свойства средств измерений, характеризующие результат измерения неизменяющихся и изменяющихся во времени величин. На рис.4.4 приведена классификация характеристик, отражающих эти свойства.

Статической характеристикой средства измерения называют функциональную зависимость между выходной величиной y и входной величиной x в установившемся режиме y = f(x). Такую зависимость еще называют уравнением шкалы прибора, градуировочной характеристикой прибора или преобразователя. Статическая характеристика может быть задана:

• аналитически;

• графически;

• в виде таблицы.

В общем случае статическая характеристика описывается зависимостью:

у = у_н + S (х – х_н), (4.1)

где у_н, х_н – начальное значение выходной и входной величины; у, х – текущее значение выходной и входной величины; S – чувствительность средства измерения.

Погрешность средства измерений ( )– это разность между показанием СИ и истинным (действительным) значением измеряемой физической величины. Погрешность и различные ее составляющие является основной нормируемой характеристикой СИ.

Чувствительность средства измерений (S) – свойство, которое количественно может быть определено как предел отношения приращения выходной величины у к приращению входной величины х:

(4.2)

На рис.4.5 приведены примеры статических характеристик средств измерений: а) и б) – линейные, в) – нелинейная. Линейность статической характеристики является важным свойством измерительного средства, обеспечивающим удобство пользования.

Нелинейность статической характеристики, особенно для технического средства измерений, допускается только тогда, когда она обусловлена физическим принципом преобразования.

Следует отметить, что для большинства средств измерений, особенно для первичных преобразователей, статическую характеристику можно считать линейной только в пределах требуемой точности измерительного средства.

Линейная статическая характеристика имеет постоянную чувствительность, не зависящую от значения измеряемой величины. В случае линейной статической характеристики чувствительность можно определить по формуле:

(4.3)

где у_к, х_к – конечное значение выходной и входной величины; у_д = у_к – у_н – диапазон изменения выходного сигнала; х_д = х_к – х_н – диапазон изменения входного сигнала.

у

у

у

у_к

х_к

у_н

х_н

у_к

у_к

x

х

у_н

x

х_к

х_к

х_н

а) б) в)

Рис. 4.5. Статические характеристики средств измерений:

а), б) – линейные; в) - нелинейные

Диапазон измерений – область значений измеряемой величины, в пределах которой нормированы допускаемые пределы погрешности средств измерений. Диапазон измерений измерительного прибора всегда меньше или равен диапазону показаний.

На отдельные элементы измерительных систем, выполняющих функции направленной передачи, масштабирования или нормирования измерительных сигналов распространяется понятие коэффициента передачи.

Коэффициентом передачи (к) называется отношение выходной величины y к входной величине x, т. е. к = y/x. Коэффициент передачи, как правило, имеет постоянное значение в любой точке диапазона преобразователя, а перечисленные виды преобразователей (масштабирующие, нормирующие) – линейную статическую характеристику.

Динамической характеристикой называется функциональная зависимость показаний средств измерений от изменения измеряемой величины в каждый момент времени, т.е. y() = f[x()].

Отклонение выходной величины y() от входной величины x() в динамическом режиме приведено на рис.4.6 в зависимости от закона изменения входной величины во времени [5].

Динамическая погрешность средств измерений определяется как

у() =y() – к x(), (4.4)

где кx() – выходная величина «идеального» в динамическом отношении преобразователя.

Динамический режим широкого класса средств измерений описывается линейными неоднородными дифференциальными уравнениями с постоянными коэффициентами. Динамические свойства средств измерений в теплоэнергетике наиболее часто моделируются динамическим звеном первого порядка (апериодическим звеном):

(4.5)

где Т – постоянная времени преобразования, которая показывает время выхода сигнала y() на установившееся значение после ступенчатого изменения входной величины x().

а) изменение входной величины с постоянной скоростью

б) ступенчатые изменения входной величины

в) синусоидальное изменение входной величины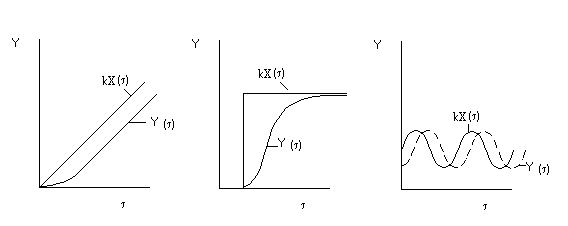

Рис. 4.6. Отклонение выходной величины от входной в динамическом режиме

Для описания динамических свойств средств измерений используют переходные характеристики. Переходная характеристика представляет собой реакцию динамической системы на единичное ступенчатое воздействие. На практике используют ступенчатые воздействия произвольного значения:

(4.6)

Переходная характеристика h() связана с реакцией линейной динамической системы y() на реальное неединичное ступенчатое воздействие соотношением:

h()=y()/X_a (4.7)

Переходная характеристика описывает инерционность измерения, обуславливающую запаздывание и искажение выходного сигнала. Переходная характеристика может иметь апериодическую и колебательную формы.

Динамические характеристики линейного средства измерений не зависят от значения и знака ступенчатого возмущения, и переходные характеристики, снятые экспериментально при различных значениях ступенчатых возмущений, должны совпадать. Если опыты при различных по значению и знаку ступенчатых возмущениях приводят к неодинаковым количественным и качественным результатам, то это свидетельствует о нелинейности исследуемого средства измерения.

Динамические характеристики средств измерений, характеризующие реакцию средства измерения на гармонические воздействия в широком диапазоне частот, называют частотными характеристиками, которые включают в себя амплитудно-частотную и фазо-частотную характеристики.

При экспериментальном определении частотных характеристик на вход средства измерений с помощью генератора подаются гармонические, например, синусоидальные колебания:

x() = A_x sin( + _x) (4.8)

Если исследуемое средство измерений является линейной динамической системой, то колебания выходной величины в установившемся режиме будут также синусоидальными (см.рис.4.6, в):

y() = A_y sin( + _y), (4.9)

где _x - начальная фаза, рад:  - угловая скорость, рад/с.

Амплитуда выходных колебаний и фазовый сдвиг зависят от свойств средства измерений и частоты входных колебаний.

Зависимость A(), показывающая, как изменяется с частотой отношение амплитуды выходных колебаний A_y() линейной динамической системы к амплитуде входных колебаний A_x() , называется амплитудно-частотной характеристикой (АЧХ) этой системы:

A() = A_y()/A_x() (4.10)

Зависимость от частоты сдвига по фазе между входными и выходными колебаниями называется фазо-частотной характеристикой (ФЧХ) системы:

() = _y() – _x() (4.11)

Частотные характеристики определяются как экспериментально, так и теоретически, по дифференциальному уравнению, описывающему связь выходного и входного сигнала (4.5). Порядок получения частотных характеристик по дифференциальному уравнению линейной системы подробно описан в литературе, посвященной теории автоматического регулирования.

На рисунке 4.7 приведены типичные частотные характеристики для средства измерения, динамические свойства которого соответствуют линейному дифференциальному уравнению первого порядка (4.5). С ростом частоты входного сигнала такое средство измерения обычно уменьшает амплитуду выходного сигнала, но увеличивает сдвиг выходного сигнала относительного входного, что приводит к возрастанию динамической погрешности.

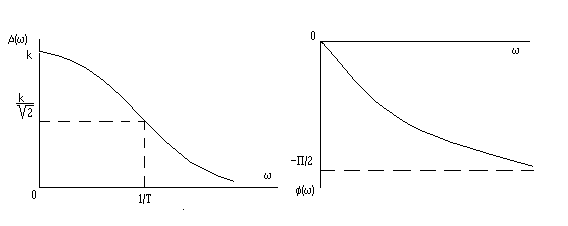
а) б)

Рис. 4.7. Амплитудно-частотная (а) и фазо-частотная (б) характеристики измерительного средства, динамические свойства которого соответствуют линейному звену первого порядка (апериодическому звену).

Покажем на примере, как выполняется оценка динамических характеристик измерительных средств, динамические свойства которых могут моделироваться линейным звеном 1-го порядка.

Пример. Расчет постоянной времени Т термоприемника.

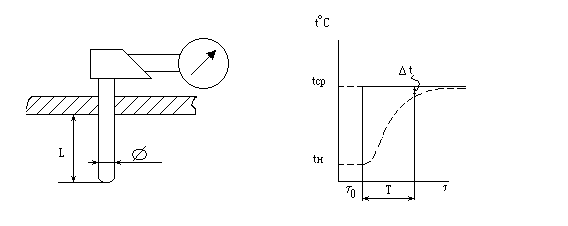
Рис. 4.8. Принципиальная схема и динамическая характеристика термоприемника

Тепловая инерция термоприемника обусловлена более медленным нагревом по сравнению с быстрым (скачкообразным) изменением температуры среды, что приводит к запаздыванию показаний прибора, измеряющего температуру.

Динамическая погрешность термоприемника определяется

где с, , S – теплоемкость, плотность, объем и площадь поверхности теплоприемника;  - коэффициент теплоотдачи; t_ср и t_пр – температуры среды и термоприемника.

Постоянная времени термоприемника определяется условием t_пр(Т)=0,63(t_ср-t_н) и равна

,

где  - толщина стенок чехла термоприемника.

Пусть дано:  = 710³ кг/м³; с = 0,400 кДж/кгград;  = 200 вт/м²град; = 2,0 мм.

Расчетная величина постоянной времени:

с.

Если температура среды t_ср = 520^оС измеряется электронным потенциометром с погрешностью  = 5^оС, то время установления показаний прибора Т_у определяется

с.