3.2Случайные погрешности. Вероятностный подход к их описанию

3.2.1Распределение случайных погрешностей

При проведении в одинаковых условиях повторных измерений одной и той же постоянной величины (температуры, расхода среды и др.) получаем отличные друг от друга результаты, хотя некоторые из них совпадают. Такие расхождения в результатах измерений говорят о наличии в них случайных погрешностей.

Каждая случайная погрешность возникает при одновременном воздействии многих источников случайных возмущений. Каждый из этих источников сам по себе оказывает незаметное влияние на результат измерения, но суммарное воздействие всех источников может оказаться сильным.

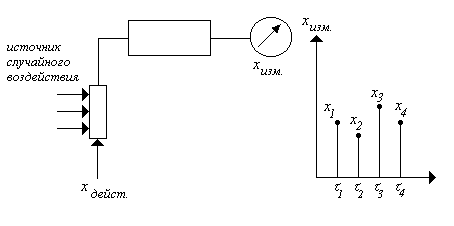
х_изм = х_дейст.  х_i

х_i – случайное отклонение измеряемой величины от действительной.

Рис. 3.1.

Методы теории вероятностей и математической статистики позволяют дать соответствующие количественные оценки случайным погрешностям как случайным величинам [2].

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения случайной величины, его интегральную и дифференциальную форму.

Интегральная функция распределения F(x) определяет вероятность попадания случайной величины х в интервал от - до х₁:

(3.2)

Дифференциальная функция распределения или плотность распределения вероятностей определяется и подчиняется условию нормирования:

(3.3)

Вероятность попадания случайной величины в заданный интервал (х₁;х₂) равна

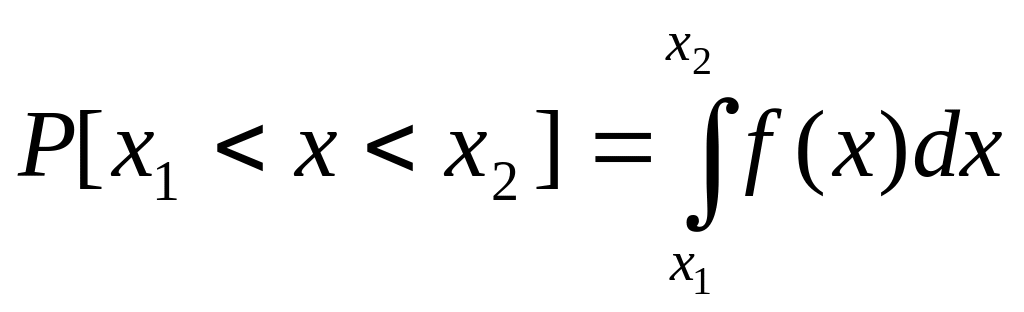, (3.4)

т.е. равна площади, заключенной под кривой f(x) между абсциссами х₁ и х₂ (см. рис.3.2.).

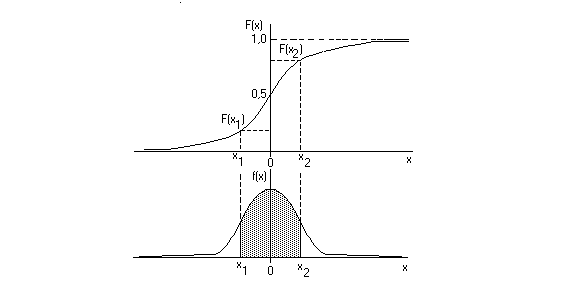
Рис. 3.2 Интегральная и дифференциальная функция распределения случайной величины х.

Для описания случайной величины используют числовые характеристики распределений – моменты случайных величин. Все они представляют собой некоторые средние значения.

Начальные моменты отсчитываются от начала координат. Наибольший интерес из них представляет математическое ожидание случайной величины

(3.5)

Центральные моменты отсчитываются от центра закона распределения; здесь важную роль играет дисперсия случайной величины

(3.6)

Положительное значение корня квадратного из значения дисперсии называется стандартным или средним квадратичным отклонением. Оно является общепринятой мерой случайной погрешности измерения

(3.7)

При выборе закона распределения случайной величины используют опыт длительных наблюдений, результаты которого выражаются в умозаключениях об особенностях распределения этой величины.

Теория случайных погрешностей и методы их оценки основаны на двух аксиомах: аксиоме случайности и аксиоме распределения.

Аксиома случайности: при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто, т.е. число отрицательных погрешностей равно числу положительных.

Аксиома распределения: малые погрешности случаются чаще, чем большие, очень большие погрешности не встречаются

Эти аксиомы указывают на два основных свойства распределения случайных погрешностей и самих результатов измерения:

• среднее значение случайных погрешностей при бесконечно большом числе измерений стремится к нулю, а измеренное значение к истинному значению измеряемой величины;

• распределение случайных погрешностей является равносторонним по отношению к среднему значению измерений.

Математическим следствием из приведенных умозаключений является использование нормального закона распределения для описания распределения результатов наблюдений, полученных при повторных измерениях (график плотности нормального распределения приведен на рис.3.3):

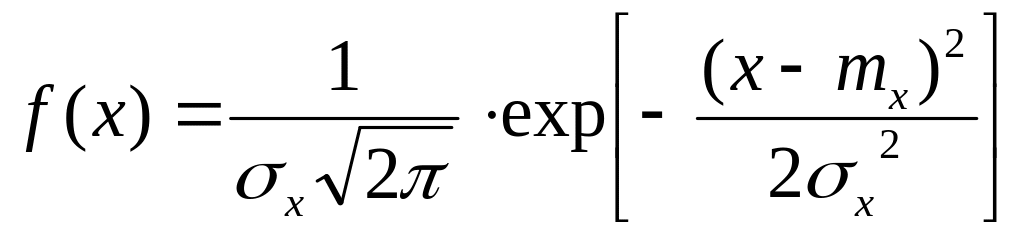
(3.8)

,

где х – результат наблюдения; - стандартное отклонение результатов наблюдений, полученных при повторных измерениях; - математическое ожидание результатов наблюдений, полученных при повторных измерениях.

Для вычисления значения интегральной функции нормального распределения используют таблицы функции Лапласа (Приложение 3), связанной с соотношением

. (3.9)

Применительно к измерениям нормальное распределение f(x) оправдано тогда, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим. Практически суммарное воздействие даже сравнительно небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному.

Перенеся начало координат в центр распределения m_x, и откладывая по оси абсцисс погрешность х = х - m_x, получим кривую нормального распределения погрешностей

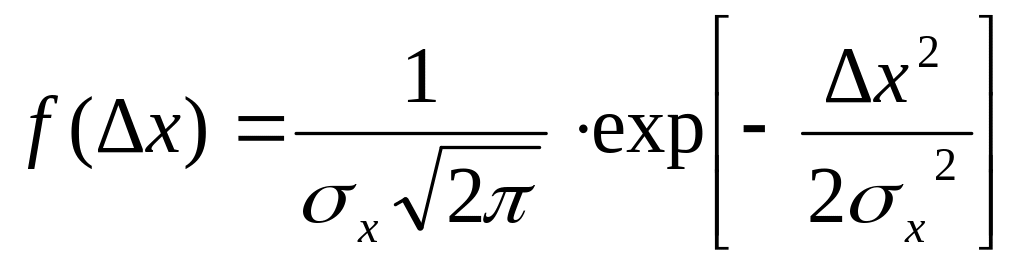(3.10)

где х – случайная погрешность результата наблюдения; - стандартное отклонение результатов наблюдений, полученных при повторных измерениях, оно же является стандартным отклонением самой погрешности результатов наблюдений; математическое ожидание погрешности принято равным нулю.