33. Теоремы Ферма, Ролля, Лагранжа, Коши
Теорема Ферма, что для любого натурального числа n > 2 {\displaystyle n>2} n>2 уравнение:
не имеет решений в целых ненулевых числах a , b , c {\displaystyle a,b,c}
Встречается более узкий вариант формулировки, утверждающий, что это уравнение не имеет натуральных решений. Однако очевидно, что если существует решение для целых чисел, то существует и решение в натуральных числах.
Теорема Ролля.
Пусть функция 
дифференцируема в открытом промежутке
,
на концах этого промежутка сохраняет
непрерывность и принимает одинаковые
значения: 
.
Тогда существует точка 
,
в которой производная функции
равна нулю: 
.
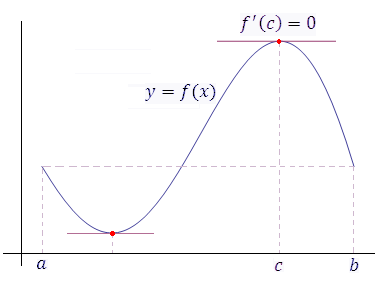Теорема
Ролля устанавливает условия существования
хотя бы одной точки c, в которой
касательная к графику функции параллельна
оси 0x. Таких точек может быть
несколько.
Доказательство. Если 
в промежутке 
,
то 
во всех точках этого промежутка. Иначе
наибольшее значение M функции
превышает ее наименьшее значение m
в промежутке
.
Поскольку на концах этого промежутка
функция
принимает одинаковые значения, то по
крайней мере одно из значений, M
или m, достигается во внутренней
точке c промежутка
.
Тогда по теореме Ферма
.
Теорема Лагранжа о среднем значении утверждает, что если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале существует хотя бы одна точка x=ξ, такая, что f(b)−f(a)=f′(ξ)(b−a). Данная теорема называется также формулой конечных приращений, поскольку она выражает приращение функции на отрезке через значение производной в промежуточной точке этого отрезка. Доказательство. Рассмотрим вспомогательную функцию F(x)=f(x)+λx. Выберем число λ таким, чтобы выполнялось условие F(a)=F(b). Тогда f(a)+λa=f(b)+λb,⇒f(b)−f(a)=λ(a−b),⇒λ=−f(b)−f(a)b−a. В результате получаем F(x)=f(x)−f(b)−f(a)b−ax.
Функция F(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и принимает одинаковые значения на концах интервала. Следовательно, для нее выполнены все условия теоремы Ролля. Тогда в интервале (a,b) существует точка ξ, такая, что F′(ξ)=0. Отсюда следует, что f′(ξ)−f(b)−f(a)b−a=0 или f(b)−f(a)=f′(ξ)(b−a).
Теорема Коши.
Пусть функции
и 
непрерывны в замкнутом промежутке
;
дифференцируемы в открытом промежутке
;
в открытом промежутке
.
Тогда существует такая точка
,
что
|
|
|
|
Доказательство. Заметим, что 
.
В противном случае – согласно теореме
Ролля – производная 
обратилась бы в нуль в некоторой точке
.
Рассмотрим
вспомогательную функцию
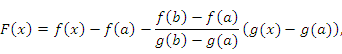
которая удовлетворяет всем условиям теоремы Ролля и, в частности, принимает одинаковые значения на концах промежутка :
Тогда существует точка , в которой
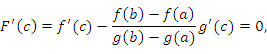
что и требовалось
доказать.
Следствие. Теорема Лагранжа является
частным случаем теоремы Коши при 
.
В свою очередь теорема Ролля представляет
собой частный случай теоремы Лагранжа.
Таким образом, теорема Коши включает
в себя в качестве частных случаев
теорему Ролля и теорему Лагранжа.