29. Производные основных элементарных функций.

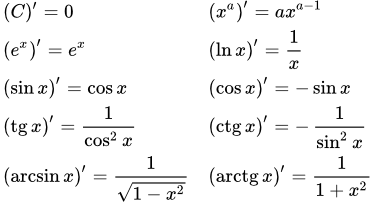
30. Дифференциал функции, геометрический смысл производной и дифференциала.

Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Э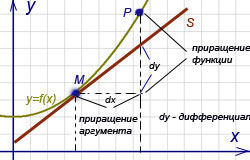 то записывается так:

или

или же

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину

Геометрический смысл производной.

Если функция y = f (x) имеет производную в точке , то есть существует конечный предел

то существует предельное положение секущей l, заданной уравнением

это означает, что в точке существует касательная к графику функции y = f (x), причём согласно формуле

, где – угловой коэффициент прямой . Так как , где – угол, образуемый касательной с положительным направлением оси абсцисс, то

Таким образом, геометрический смысл производной состоит в том, что производная функции в данной точке равна угловому коэффициенту касательной к графику функции в точке .

Уравнение касательной к графику функции y = f (x) в точке , получаемое из уравнения заменой на , имеет вид

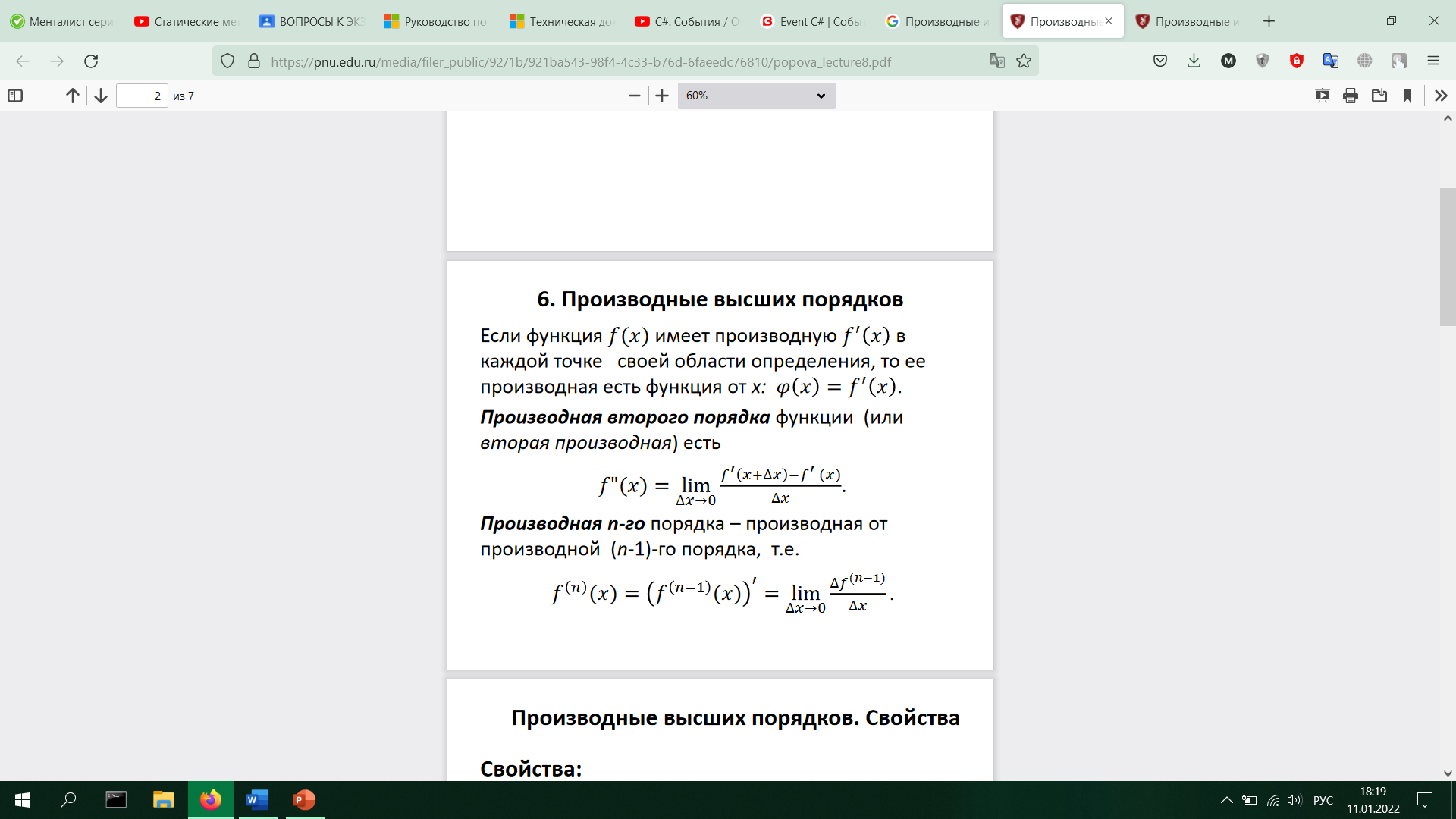
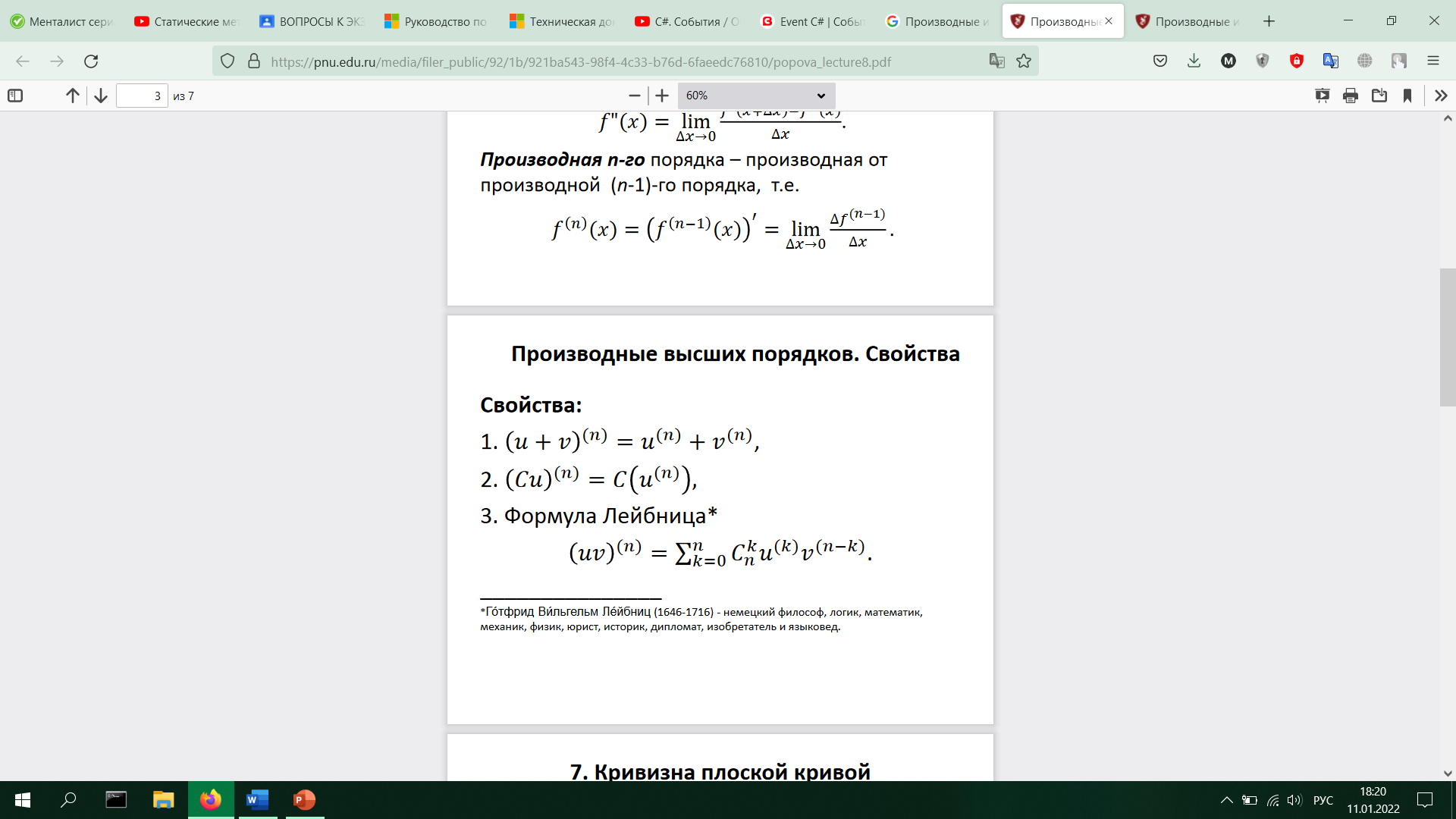
31. Производные и дифференциалы высших порядков. Формула Лейбница

32. Производные от неявно заданных функций и функций, заданных параметрически

Функция задана в явном виде

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).( х³+у³-3ху=0.)

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Функция задана параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.