25. Равномерная непрерывность. Теорема о равномерной непрерывности Кантора.

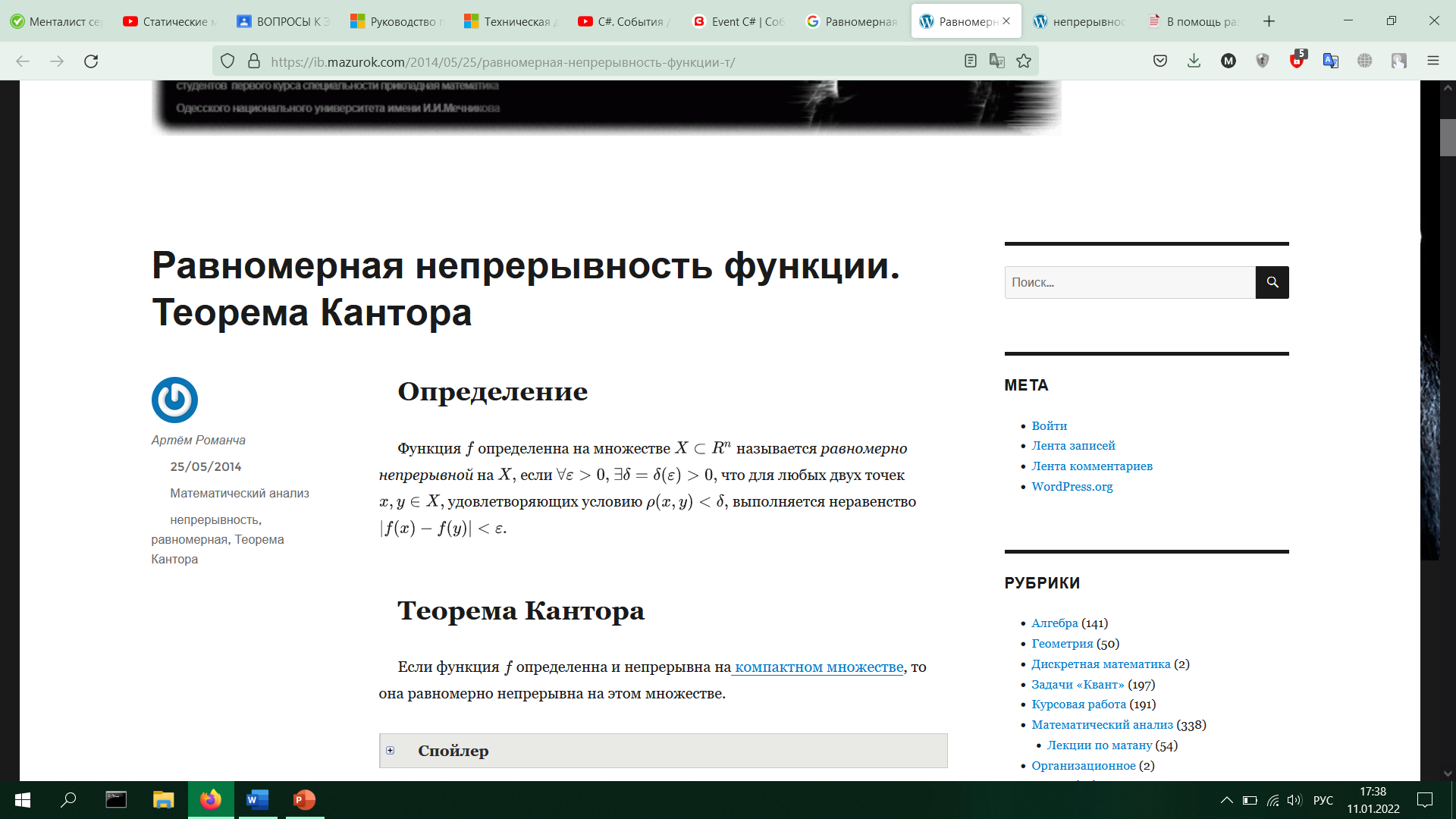
Если функция определенна и непрерывна на компактном множестве, то она равномерно непрерывна на этом множестве.

26. Непрерывность элементарных функций.

• f(x) = C, (где С – постоянная) непрерывна на R, т.к. при любом x.

• f(x) = x, непрерывна на R, т.к. при .

• f(x) = , непрерывна на R как произведение непрерывных функций.

• f(x) = , непрерывна на R, т.к. многочлен есть сумма непрерывных функций.

• f(x) = , где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций.

• f(x) = sin(x), f(x) = cos(x)

• Пусть – произвольная точка множества R. Тогда sinx-sin . Так как , а , то , откуда следует, что функция f(x) = sin(x) – непрерывна.

• Аналогично рассуждая, можно доказать непрерывность косинуса. Из непрерывностей синуса и косинуса следуют непрерывности тангенса и котангенса, учитывая что (для тангенса) и (для котангенса).

• f(x) = arcsin(x), f(x) = arccos(x), f(x) = arctg(x), f(x) = arcctg(x) , непрерывны на своей области определения. Это следует из теоремы об обратной функции, примененной не ко всей тригонометрической функции (к примеру, sin(x)), а к ее отрезку (для sin(x) это отрезок ).

• , где r – рациональное. Представим r = m / n, . Тогда . Функция непрерывна и строго возрастает на R. По п. 2 также непрерывна.

• , a > 1, непрерывна на R. Пусть – произвольная точка множества R, = . Докажем, что . Пусть - произвольная последовательность вещественных чисел такая, что . В силу свойств вещественных чисел найдутся последовательности рациональных чисел и , удовлетворяющие при условию: < , откуда Так как и , то =1. Отсюда и , ч.т.д.

• Логарифмическая функция непрерывна, что следует из непрерывности показательной функции по теореме об обратной функции.

27. Понятие производной функции в точке. Понятие дифференцируемости. Необходимое и достаточное условие дифференцируемости функции в точке.

Производной функции y=f(x) в точке x₀ называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю

28.Правила вычисления производных, связанные с арифметическими действиями над функциями. Производная обратной и сложной функций.

Если функции y₁ =  f₁(x) и y₂ =  f₂(x) заданы в окрестности точки x₀ R, а в самой точке x₀ имеют конечные производные, то функции ₁ f₁(x) + ₂ f₂(x), ₁ R, ₁ R,   f₁(x)f₂(x), а в случае f₂(x₀) 0 и функции f₁(x)/f₂(x) также имеют в точке x₀ конечные производные; при этом имеют место формулы

( 1 y1 + 2 y2)' = 1 y'1 + 2 y'2,	(10.21)
(y1y2)' = y'1y2 + y1y'2,	(10.22)
	(10.23)

(в формулах (10.21)-(10.23) значения всех функций взяты при x = x₀). Прежде всего заметим, что в силу условий теоремы в точке x₀ существуют конечные пределы

( y₁/ x) = y'₁,     ( y₂/ x) = y'₂.

Докажем теперь последовательно формулы (10.21)-(10.23).

    1) Пусть y = ₁ y₁ + ₂ y₂; тогда y = ( ₁( y₁ + y₁) + ₂( y₂ + y₂)) - ( ₁y₁ + ₂y₂) = ₁ y₁ + ₂ y₂ и, следовательно,

y₁/ x = ₁ y₁/ x + ₂ y₂/ x.

Перейдя здесь к пределу при x 0, получим формулу (10.21).     2) Пусть y₂ = y₁y₂; тогда y = ( y₁ + y₁)( y₂ + y₂)) - y₁y₂ = y₂y₁ + y₂ y₁ + y₁ y₂ + y₁ y₂, откуда

y1/ x = y2 y1/ x +  y1 y2/ x.

(10.24)

    Заметив, что в силу непрерывности функции  f₂ в точке x₀ выполняется условие y₂ = 0, и, перейдя в равенстве (10.24) к пределу при x 0, получим формулу (10.22).

    3. Пусть f₂(x₀) 0, и y = y₁/y₂; тогда

следовательно,

Перейдя здесь к пределу при x 0, получим формулу (10.23).      Отметим, что из формулы (10.21) при y₂ = 0   (так же, как и из формулы (10.22), когда функция y₂ равна постоянной, а поэтому y'₂ = 0) следует, что постоянную можно выносить из-под знака дифференцирования, т. е.

( y)' = y',   R.

Пример. Вычислим производную функции tg x. Применяя формулу (10.23), получим

Итак,

(tg x)' = 1/cos²x.

Аналогично вычисляется

(ctg x)' = -1/sin²x.

    Замечание. Поскольку dx = y'dx, то, умножая формулы (10.21)-(10.23) на dx, получим

d( ₁ y₁ + ₂ y₂) = ₁dy₁ + ₂ dy', d(y₁y₂) = y₂dy₁ + y₁dy₂,

Пусть функция удовлетворяет условиям теоремы о непрерывности сложной функции и функция является для нее обратной.

Теорема (о производной обратной функции)

Пусть функция является непрерывной и строго монотонной в некоторой окрестности точки и имеет в этой точке производную Тогда Обратная функция также имеет в соответствующей точке производную, причем

(5.3.1)

Теорема (о производной сложной функции).

Пусть функция имеет производную в точке , а функция имеет производную в соответствующей точке . Тогда сложная функция имеет Производную в точке и справедлива следующая формула:

(5.3.2)

В данной теореме рассмотрена суперпозиция двух функций, где зависит от через промежуточную переменную . Возможна и более сложная зависимость с несколькими промежуточными переменными, однако правило дифференцирования сложной функции остается тем же. Например, если то производная вычисляется по формуле

(5.3.3)