10. Понятие функции. Монотонные, четные, нечетные, ограниченные, неограниченные, сложные, обратные функции. Примеры.

Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной

Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

 

Обратная функция

Пусть функция y = f(x) определена на множестве Х и имеет множество значений У.

Если каждому значению   соответствует единственное значение   , то определена функция   с областью определения У и множеством значений Х. Такая функция   называется обратнойк функции y = f(x).

Пример 5. Функции   и   являются взаимно обратными.

Сложная функция

Пусть даны функции:

1)   с областью определения U и множеством значений У;

2)   с областью определения Х и множеством значений   , причем   .

Функция   , заданная на множестве Х, называется сложной функцией от х или суперпозицией функций   и   . Пример 6.   ,   и   .

11. Элементарные функции и их графики

12. Предел функции в точке. Эквивалентность определений по Коши и по Гейне. Односторонние пределы.

Предел функции в точке. Эквивалентность определений по Коши и по Гейне.

Односторонние пределы.

Эквивалентность определений по Коши и по Гейне.

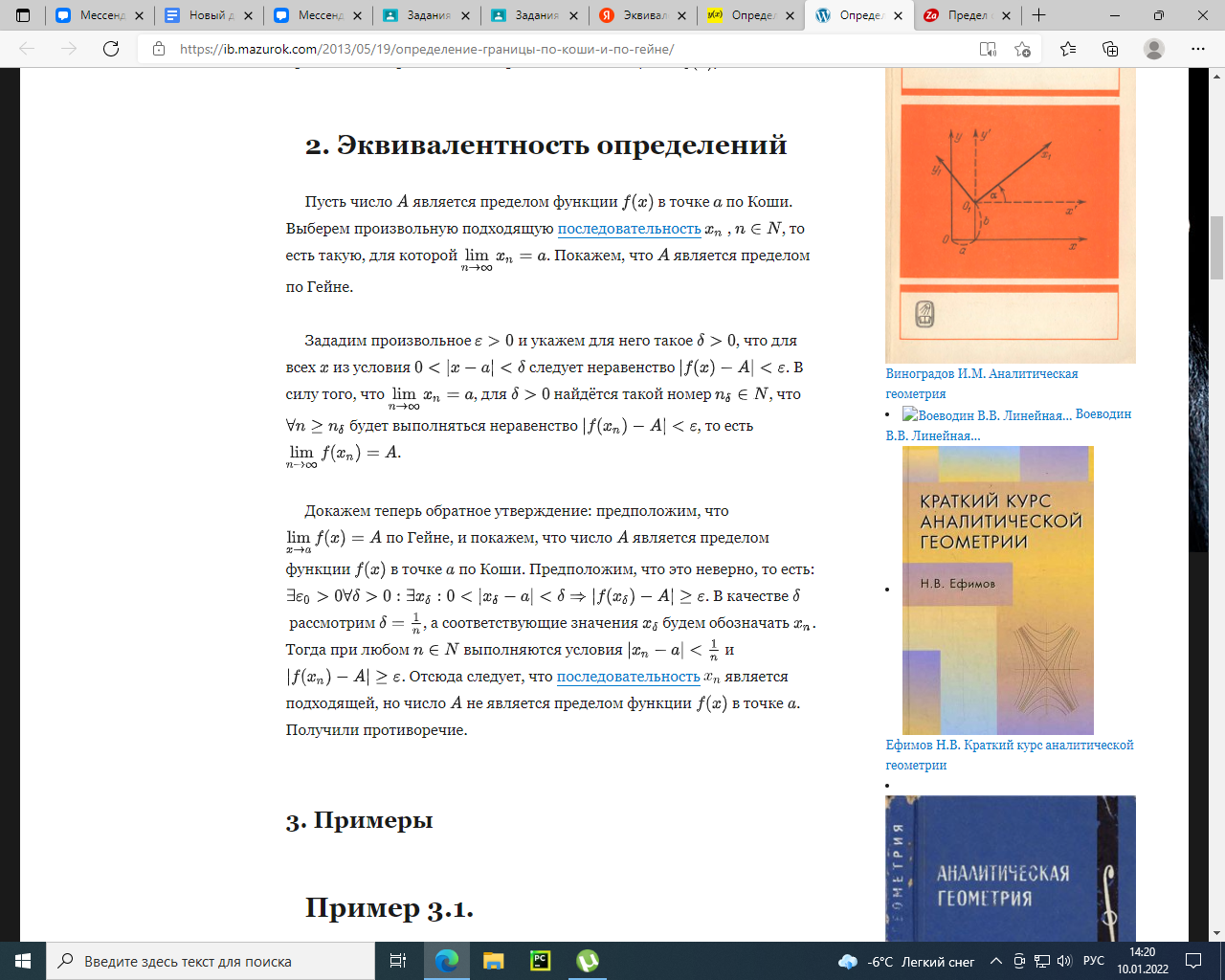
Односторонние пределы.

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

13. Критерий Коши существования предела функции.

14. Свойства пределов функции в точке. Правило замены переменного для

пределов функций.

Правило замены переменного для пределов функций.

15. Первый замечательный предел.

16. Второй замечательный предел.

17. Бесконечно малые и бесконечно большие функции. Сравнение функций. Свойства о (малое).

Сравнение функций.?

18. Применение эквивалентных бесконечно малых к вычислению пределов.

Таблица эквивалентных бесконечно малых.

19. Теорема о пределе монотонных функций.

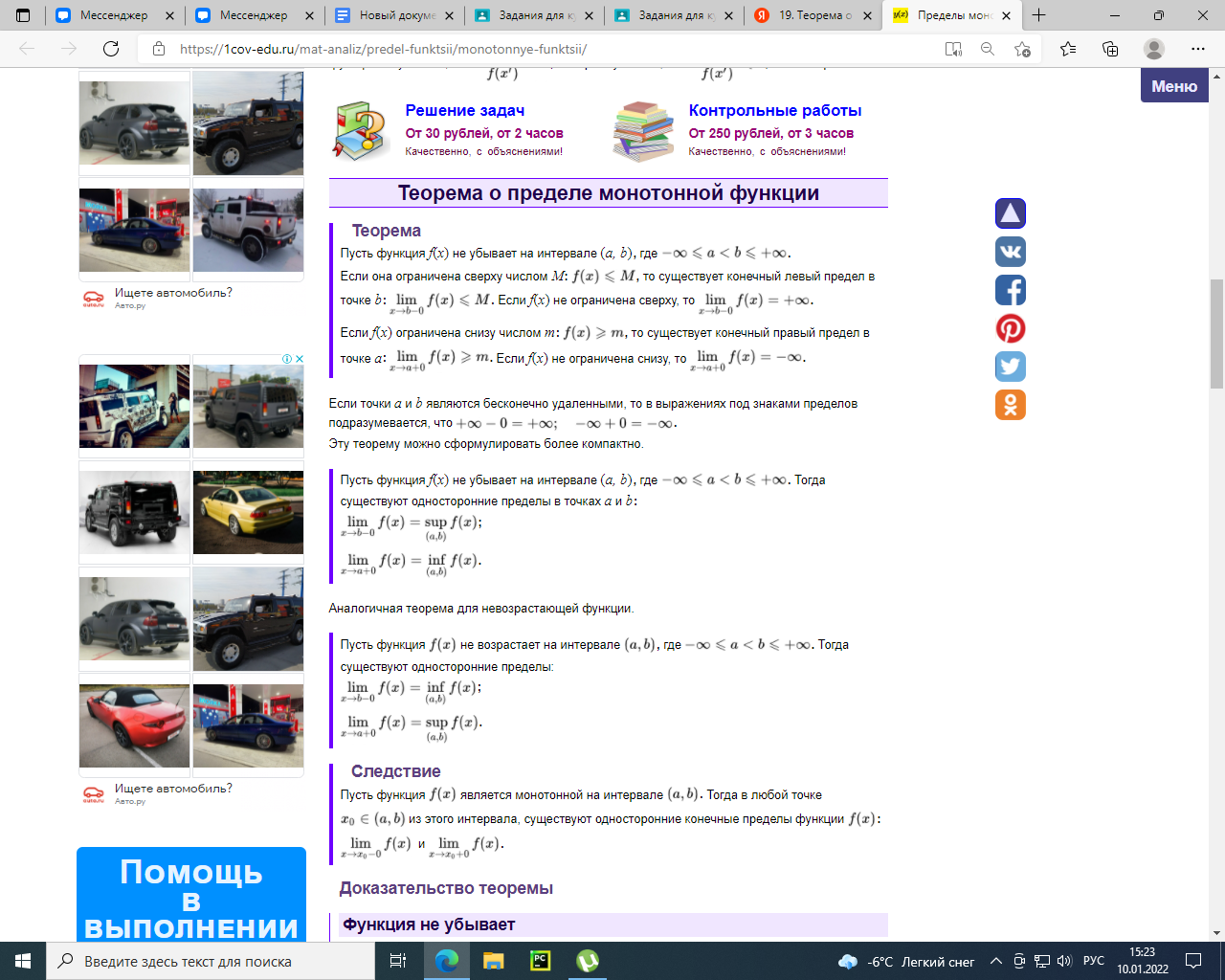
20. Непрерывность функции в точке. Определения по Коши и Гейне, непрерывность слева и справа. Свойства непрерывных функций.

Определения по Коши и Гейне, непрерывность слева и справа.

Свойства непрерывных функций.

21. Разрывные функции. Классификация точек разрыва. Примеры.

РАЗРЫВНЫЕ ФУНКЦИИ- функции, имеющие разрыв в нек-рых точках .

Классификация точек разрыва

Примеры.

22. Непрерывность функции на отрезке. Теорема об ограниченности непрерывной функции.

23. Теорема о достижении непрерывной функцией максимума и минимума на отрезке.

24. Теорема о непрерывности обратной функции.

Теорема об обратной ф-ции.

Если функция непрерывна и строго возрастает на отрезке , то на отрезке определена функция , обратная к f, непрерывная и строго возрастающая.

Непрерывность обратной функции. Пусть — произвольная точка интервала (A,B). Докажем, что функция g непрерывна в точке . Для этого достаточно показать, что справедливы равенства

(29) где и пределы функции g соответственно слева

и справа в точке .

По теореме о пределах монотонной функции (§ 10) пределы функции g слева и справа в точке существуют и выполняются неравенства

Пусть хотя бы одно из равенств (29) не выполняется, например, , тогда

(31)

Так как для всех выполняется неравенство , где а при всех справедливо неравенство , то из условия (31) следует, что интервал не принадлежит множеству значений

функции g. Это противоречит тому, что все точки отрезка [a,b], в том числе и точки интервала , принадлежат множеству E(g). Итак, первое из равенств (29) доказано. Аналогично доказывается справедливость второго из равенств (29). Тем же способом устанавливается, что функция g непрерывна справа в точке A и непрерывна слева в точке B.

Замечание 6. Если функция f непрерывна и строго убывает на отрезке [a,b], то обратная к ней функция g непрерывна и строго убывает на отрезке

Замечание 7. Аналогично формулируется и доказывается теорема о функции g, обратной к функции f, для случаев, когда функция f задана на интервале (конечном либо бесконечном) и полуинтервале.

Если функция f определена, строго возрастает и непрерывна на интервале (a,b), то обратная функция g определена, строго возрастает и непрерывна на интервале (A,B), где , .