1. Вещественные числа. Грани числового множества. Теорема о существовании точной верхней и нижней граней. Операции над вещественными числами, свойства операций.

Вещественные числа – это множество рациональных и нерациональных чисел(проще говоря числа, имеющие дробную часть), использующихся для измерения физических и геометрических величин

Говорят, что множество   ограничено сверху (снизу), если существует такое число  , что   для любого  . Число   в этом случае называется верхней (нижней) гранью множества X.

Теорема о существовании точных граней ограниченного множества :

Всякое ограниченное сверху непустое числовое множество имеет точную верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет точную нижнюю грань.

Существует несколько операций над вещественными числами: сложение, вычитание, деление, умножение и возведение в степень.

Свойства операций:

1°.   (переместительное свойство). 2°.   (сочетательное свойство). 3°.   (переместительное свойство). 4°.   (сочетательное свойство). 5°.   (распределительное свойство). 6°. Существует единственное число 0 такое, что а + 0=а для любого числа а. 7°. Для любого числа а существует такое число (—а), что а+(-а) = 0. 8°. Существует единственное число   такое, что для любого числа а имеет место равенство а • 1 = а. 9°. Для любого числа  существует такое число   что   число   обозначают также символом 

2. Понятие комплексного числа. Различные формы записи. Арифметические операции над комплексными числами, возведение в степень и извлечение корня.

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i 2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.

Запись комплексного числа в видеz =a + ib принято называть алгебраической формой записи комплексного числа, а запись в виде z= r (cosϕ + i*sinϕ)– тригонометрической формой записи.

Операции над комплексными числами:

1)Сложение и вычитание :

z1+z2 = (a1+b1i)+(a2+b2i) = (a1+a2)+(b1+b2)i

z1-z2 = (a1+b1i)-(a2+b2i) = (a1-a2)+(b1-b2)i

2) Произведение

z1*z2=r1*r2*[cos(α1+ α2) + i*sin(a1+a2)]

3)Частное

4)Возведение в степень

5)Корень комплексного числа

3. Грани числового множества. Теорема о существовании точной верхней и нижней граней. Принцип вложенных отрезков.

Теорема о существовании точных граней ограниченного множества :

Всякое ограниченное сверху непустое числовое множество имеет точную верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет точную нижнюю грань.

Существует несколько операций над вещественными числами: сложение, вычитание, деление, умножение и возведение в степень.

Свойства операций:

1°.   (переместительное свойство). 2°.   (сочетательное свойство). 3°.   (переместительное свойство). 4°.   (сочетательное свойство). 5°.   (распределительное свойство). 6°. Существует единственное число 0 такое, что а + 0=а для любого числа а. 7°. Для любого числа а существует такое число (—а), что а+(-а) = 0. 8°. Существует единственное число   такое, что для любого числа а имеет место равенство а • 1 = а. 9°. Для любого числа  существует такое число   что   число   обозначают также символом 

Лемма о вложенных отрезках (принцип Коши – Кантора). Для любой последовательности вложенных отрезков существует точка, принадлежащая всем этим отрезкам. Если длины отрезков стремятся к нулю:, то такая точка единственная.

4. Понятие числовой последовательности. Монотонные и ограниченные последовательности. Бесконечно малые и бесконечно большие числовые последовательности, их свойства.Сходящиеся последовательности. Ограниченность, единственность предела. Арифметические действия с пределами.

Числовая последовательность – это последовательность чисел.

Ограниченные последовательности: Последовательность аn называется ограниченной, если для любого n ∈ N существуют числа m M(соответственно нижняя и верхняя границы последовательности) такие, что выполняется неравенство m<an< M.

Монотонные последовательности: Последовательность аn=f(n) называется возрастающей(неубывающей), если аn<an+1для любого n ∈ N, иубывающей(невозрастающей) , если an>an+1 для любого n ∈ N .

Последовательность     называется бесконечно малой , если значения всех ее элементов – начиная с некоторого номера – становятся по абсолютной величине меньшими любого положительного числа ε.

Свойства бесконечно малых :

Свойство 1. Произведение бесконечно малой последовательности    и ограниченной последовательнос ти    есть бесконечно малая последовательность  . 

Следствие. Умножение бесконечно малой последовательности на любое число дает бесконечно малую последовательность.

Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая. 

Последовательность    называется бесконечно большой , если абсолютные величины всех ее элементов – начиная с некоторого номера  N  – превышают любое сколь угодно большое наперед заданное число  E > 0. Другими словами, 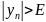    при  n > N.        Легко показать, что общий член    бесконечно большой последовательности может быть представлен в виде

где   –некоторая бесконечно малая последовательность. 

Последовательность называется сходящейся, если существует такое число , что в любой -окрестности точки находятся все элементы последовательности, начиная с некоторого номера.

Числовая последовательность    называется ограниченной, если множество членов этой последовательности образует ограниченное множество.

Единственность предела последовательности.

Арифметические действия с пределами.