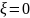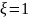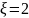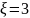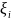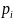МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
КАФЕДРА 2
|
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
Доктор физико-математических наук, профессор |
|
|
|
Фарафонов В. Г. |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
КОНТРОЛЬНАЯ РАБОТА
|
Основы теории вероятностей и математической статистики
|
по дисциплине: Математика. Теория вероятностей и математическая статистика |
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
9411 |
|
|
|
Кафка Р. С. |
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
Студенческий билет № |
2019/3603 |
|
|
|
|
Шифр ИНДО |
|
Санкт-Петербург 2020
Вариант 3
Бросают игральную кость. Путь событие А – это выпадение четного числа, а событие В – выпадение числа большего 3. Что представляют собой события A̅, B̅, A∪B, A∩B, A\B, B\A? Какие элементы пространства элементарных исходов данного опыта им благоприятствуют?
Решение:
Найдём общее число исходов:
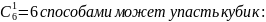
(1), (2), (3), (4), (5), (6).
Событию А соответствует три благоприятствующих исхода:
(2), (4), (6)
Событию B соответствует три благоприятствующих исхода:
(4), (5), (6)
A̅ = (1), (3), (5) – выпадение нечётного числа.
B̅ = (1), (2), (3) – без чисел, которые больше 3.
A∪B = (2), (4), (5), (6) – объединение событий, наступает хотя бы одно событие.
A∩B = (4), (6) – пересечение событий, одновременное наступление событий.
A\B = (2) – разность событий. А происходит, а B не происходит.
B\A = (5) – разность событий. B происходит, а A не происходит.
Бросают две игральные кости. Найти вероятность события A, когда сумма выпавших очков равна 5, и события B, когда произведение выпавших очков равно 4.
Решение:
Найдём общее число исходов:
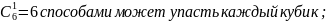
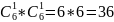 комбинаций
цифр может выпасть при одновременном
броске двух кубиков.
комбинаций
цифр может выпасть при одновременном
броске двух кубиков.
Событию А соответствует четыре благоприятствующих исхода:
(1,4), (2,3), (3,2), (4,1)
По классическому определению вероятности:
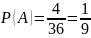 – вероятность
того, что сумма выпавших очков равна 5.
– вероятность
того, что сумма выпавших очков равна 5.
Событию B соответствует три благоприятствующих исхода:
(1,4), (4,1), (2,2)
По классическому определению вероятности:
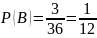 – вероятность
того, что произведение выпавших очков
равно 4.
– вероятность
того, что произведение выпавших очков
равно 4.
Ответ:
 ,
,
 .
.
Случайным образом выбирают 3 шара из 8, среди которых 3 белых и 5 черных. Найти вероятность того, что среди выбранных окажется два белых шара.
Решение:
Всего 8 шаров.
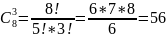 способами
можно извлечь 3 шара.
способами
можно извлечь 3 шара.
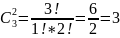 способами
можно извлечь 2 белых шара.
способами
можно извлечь 2 белых шара.
По классическому определению:
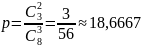 -
вероятность того, что будут извлечены
2 белых шара
-
вероятность того, что будут извлечены
2 белых шара
Ответ:
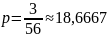
Два независимых события A и B наступают с вероятностями 0,4 и 0,8 соответственно. Найти вероятность того, что наступит: а) хотя бы одно событие; б) ровно одно событие.
Решение:
По
условию
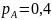 ,
,
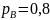 –
вероятности наступления событий. Тогда
вероятности того, что они не наступят:
–
вероятности наступления событий. Тогда
вероятности того, что они не наступят:
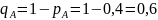 ;
;
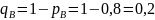
а) По теореме умножения вероятностей независимых событий:
 – вероятность
того, что оба события не наступят.
– вероятность
того, что оба события не наступят.
Найдём вероятность противоположного события:
 – вероятность
того, что наступит хотя бы одно событие.
– вероятность
того, что наступит хотя бы одно событие.
б) По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
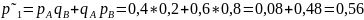 – вероятность
того, что наступит ровно одно событие.
– вероятность
того, что наступит ровно одно событие.
Ответ:
а)
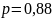 б)
б)
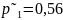
В группе 20 студентов: 2 отличника, 8 хорошистов, 6 троечников и 4 двоечника. Отличники учат 100% экзаменационных билетов, хорошисты – только 80%, троечники – 60% и двоечники – только 40%. Найти вероятность того, что взятый наугад студент этой группы сдаст экзамен. Если некий студент данной группы сдал экзамен, то какова вероятность того, что он являлся одним из шести троечников?
Решение:
Из
условия находим
 – вероятности выбора отличника,
хорошиста, троечника и двоечника
соответственно.
– вероятности выбора отличника,
хорошиста, троечника и двоечника
соответственно.
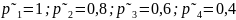 – вероятности
того, что отличник, хорошист, троечник
и двоечник соответственно сдаст экзамен.
– вероятности
того, что отличник, хорошист, троечник
и двоечник соответственно сдаст экзамен.
По формуле полной вероятности:
 – вероятность
того, что взятый наугад студент этой
группы сдаст экзамен.
– вероятность
того, что взятый наугад студент этой
группы сдаст экзамен.
По формуле Байеса:
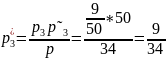 – вероятность
того, что сдавший экзамен студент являлся
одним из шести троечников.
– вероятность
того, что сдавший экзамен студент являлся
одним из шести троечников.
Ответ:
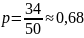 ,
, 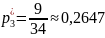
Известна вероятность события A: p(A) = 0,3. Дискретная случайная величина ξ – число появлений события A в трех опытах. Требуется построить ряд распределения этой случайной величины, найти ее математическое ожидание M[ξ], дисперсию D[ξ], среднее квадратическое отклонение σ и вероятность попадания в интервал p(|ξ – M[ξ]| < σ).
Решение:
Случайная величина ξ имеет биномиальное распределение. Найдем закон распределения случайной величины ξ, используя формулу Бернулли:
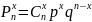
В данной задаче:
 – всего
опытов;
– всего
опытов;
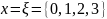 – вероятное
количество появлений событий.
– вероятное
количество появлений событий.
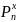 – вероятность
того, что из n
опытов появится ровно ξ
событий.
– вероятность
того, что из n
опытов появится ровно ξ
событий.
По условию:
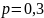 – вероятность
события.
– вероятность
события.
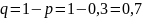 – вероятность
события не появиться.
– вероятность
события не появиться.
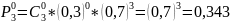
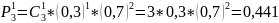
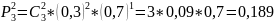

Таким образом, искомый закон распределения:
|
0 |
1 |
2 |
3 |
|
0,343 |
0,441 |
0,189 |
0,027 |
Проверка: 0,343+0,441+0,189+0,027=1
Составим функцию распределения:

Вычислим математическое ожидание M(ξ), дисперсию D(ξ) и среднее квадратическое отклонение σ(ξ).
Вычислим
математическое ожидание:
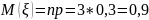
Найдём
дисперсию:
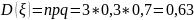
Среднее
квадратическое отклонение: