МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
(ГУАП)
КАФЕДРА № 44
Преподаватель
канд. техн. наук, доцент Бариков Л. Н.
Отчёт
по лабораторной работе №11
по дисциплине ОСНОВЫ ПРОГРАММИРОВАНИЯ
на тему: «Передача имен функций в качестве параметров»
Работу выполнил
студент гр. Z9411 Кафка Р. С.
Санкт-Петербург
2020
Лабораторная работа №11 Передача имён функций в качестве параметров
Цель лабораторной работы: изучение методов передачи имён функций в качестве параметров других функций; изучение методов нахождения приближённого значения определённого интеграла произвольной функции на заданном интервале и с заданной точностью; совершенствование навыков процедурного программирования на языке C/C++ при решении задач с использованием рекурсивных функций.
Задание на программирование: используя технологию процедурного программирования реализовать заданный метод нахождения значения определённого интеграла произвольной функции на заданном интервале и с заданной точностью и применить его для определения площадей областей на плоскости в соответствии с индивидуальным заданием.
Порядок выполнения работы:
1. Получить у преподавателя индивидуальное задание:
- метод нахождения значения определённого интеграла произвольной функции на заданном интервале интегрирования и с заданной точностью;
- задачу определения места нахождения точки с произвольно заданными координатами на координатной плоскости (вариант и формулировка этой задачи берётся из лабораторной работы №2).
2. Разработать математическую модель:
- привести уравнения линий, ограничивающих выделенные штриховкой области;
- описать условия попадания точки в каждую выделенную область;
- составить аналитические формулы определения площади каждой выделенной области;
- определить аналитический вид функций, графики которых соответствуют линиям, ограничивающим выделенные штриховкой области;
- определить площадь каждой выделенной области с использованием значений определённых интегралов соответствующих функций на заданном интервале интегрирования и с заданной точностью.
3. Составить программу на языке C/C++.
4. Входные данные должны вводиться с клавиатуры по запросу.
5. Выходные данные (сообщения) должны выводиться на экран в развернутой форме. Операторы вывода результатов работы должны находиться либо в функции main(), либо в специальной функции вывода, вызов которой осуществляется из функции main().
6. Проверить и продемонстрировать преподавателю работу программы на полном наборе тестов.
7. Оформить отчет о лабораторной работе в составе: постановка задачи, математическая модель, текст программы, контрольные примеры (скриншоты).
Вариант индивидуального задания 4. Метод определения значения определённого интеграла
4. Метод криволинейных трапеций.
Вид областей на координатной плоскости №4
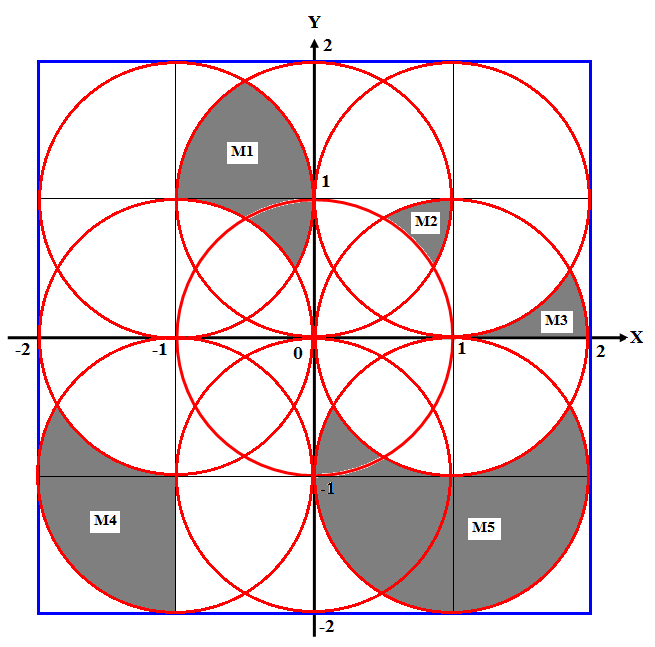
Математическая модель решения задачи определения приближённого значения определённого интеграла функции y=f(x) на интервале [a, b]
Как известно, абсолютная величина значения определённого интеграла для функции y=f(x) на интервале [a, b] численно равна площади под линией, описывающей поведение функции y=f(x), относительно оси x на этом интервале. На рисунке 1 это площадь заштрихованной области.

Рисунок 1
Для произвольного вида функции y=f(x) это значение может быть вычислено только с некоторой точностью одним из следующих способов.
Прежде всего, исходный интервал интегрирования [a, b] разбивается на произвольное количество частей с шагом h=(b-a)/n (рисунок 2):
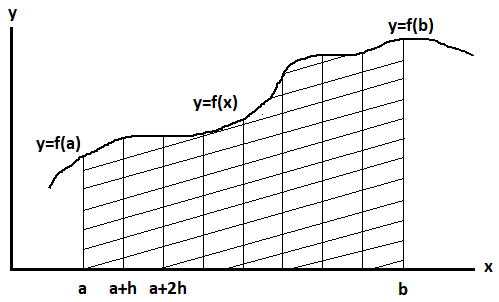
Рисунок 2
Искомая площадь под линией y=f(x) на интервале [a, b] относительно оси x будет равна сумме площадей, вычисленных на интервалах [a, a+h], [a+h, a+2h], …, [a+(n-1)h, b].
Приближённое значение площадей на этих интервалах может быть определено одним из следующих методов:
- метод левых прямоугольников (рисунок 3а);
- метод правых прямоугольников (рисунок 3б);
- метод прямоугольных трапеций (рисунок 3в);
- метод криволинейных трапеций (рисунок 3г).
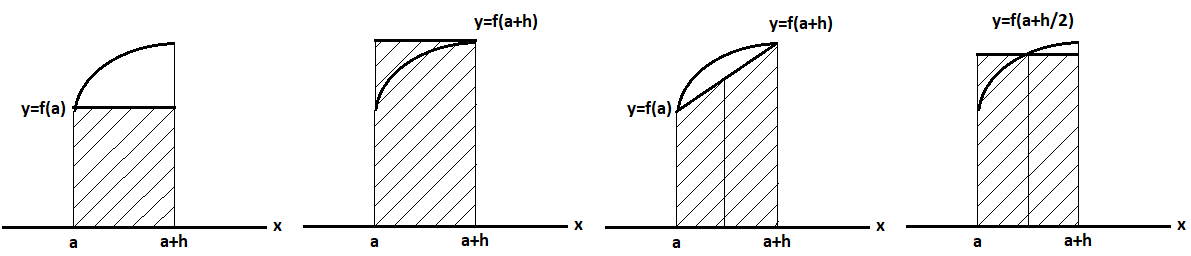
а) б) в) г)
Рисунок 3
Во всех этих приближённых методах вычисление искомой площади криволинейной трапеции заменяется вычислением площади прямоугольника, одна сторона которого равна h, а вторая сторона равна:
- в первом случае: f(a),
- во втором: f(a+h),
- в третьем случае: (f(a)+f(a+h))/2,
- в четвёртом случае: f(a+h/2),
Чем больше величина n, тем меньше будет значение h и тем точнее будет вычислена площадь криволинейной трапеции на интервале [a, a+h].
Последовательность действий следующая. Из интервала (0, 0.1] задают требуемую точность вычисления ɛ. Затем задают произвольное значение числа разбиения n интервала [a, b] (шаг разбиения h=(b-a)/n) и одним из указанных методов вычисляют значение искомой площади s1. После этого увеличивают значение n в два раза (уменьшают шаг разбиения h в два раза), и снова вычисляют значение площади s2.
Сравнивают абсолютную величину разности этих площадей с заданной точностью вычисления. Если |s2-s1|>ɛ, опять увеличивают значение n в два раза (уменьшают шаг разбиения h ещё в два раза), и снова вычисляют значение площади. Сравнивают это значение с предыдущим вычисленным значением, и при необходимости повторяют все действия.
Процесс завершается при достижении соотношения |s2-s1|≤ɛ.
Таким образом, для определения площадей выделенных областей на плоскости необходимо для каждой из них задать вид функций y=f(x), описывающих границы этих областей. После этого каждую выделенную область необходимо представить как сумму (разность) областей, площади которых можно определить указанным методом. Для каждой из них необходимо задать значения интервалов интегрирования функций y=f(x).
Пример разработки математической модели решения задачи для варианта задания вида:
Математическая модель решения
- условие 1 (принадлежность области М1):
(x+1)2+(y-1)2<1 {внутри левой верхней окружности}
x2+(y-1)2<1 {внутри верхней окружности}
(x+1)2+y2>1 {вне левой окружности}
Аналитическое выражение определения площади области М1:
площадь
сектора 1200
(πr2/3)
– площадь треугольника ( /2×0.5)
+ четверть площади круга (πr2/4)
- (площадь сектора 1200
(πr2/3)
- площадь треугольника (
/2×0.5))
= π/3–
/2×0.5
+ π/4 – (π/3-
/2×0.5)
= π/4 ≈ 0.7853
/2×0.5)
+ четверть площади круга (πr2/4)
- (площадь сектора 1200
(πr2/3)
- площадь треугольника (
/2×0.5))
= π/3–
/2×0.5
+ π/4 – (π/3-
/2×0.5)
= π/4 ≈ 0.7853
Аналитический вид функций, подлежащих интегрированию:
 {верхняя
полуокружность левой верхней окружности};
интервал интегрирования [-0.5, 0]; результат
s1.
{верхняя
полуокружность левой верхней окружности};
интервал интегрирования [-0.5, 0]; результат
s1.
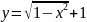 {верхняя
полуокружность центральной верхней
окружности}; интервал интегрирования
[-1, -0.5]; результат s2.
{верхняя
полуокружность центральной верхней
окружности}; интервал интегрирования
[-1, -0.5]; результат s2.
 {верхняя
полуокружность левой центральной
окружности}; интервал интегрирования
[-1, (
/2)-1];
результат s3.
{верхняя
полуокружность левой центральной
окружности}; интервал интегрирования
[-1, (
/2)-1];
результат s3.
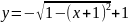 {нижняя
полуокружность левой верхней окружности};
интервал интегрирования [(
/2)-1,
0]; результат s1.
{нижняя
полуокружность левой верхней окружности};
интервал интегрирования [(
/2)-1,
0]; результат s1.
Площадь области M1= s1+s2-s3-s4.
- условие 2 (принадлежность области М2):
x2+(y-1)2<1 {внутри верхней окружности}
(x-1)2+y2<1 {внутри правой окружности}
x2+y2>1 {вне центральной окружности}
Аналитическое выражение определения площади области М2:
площадь квадрата (1×1) - четверть площади круга (πr2/4) – 2×(площадь прямоугольника (1×(1- /2)) – площадь сектора 600 (πr2/6) + площадь треугольника ( /2×0.5))=1-π/4–2×(1- /4-π/6)= /2+π/3-π/4–1≈0.1278
Аналитический вид функций, подлежащих интегрированию:
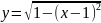 {верхняя
полуокружность правой центральной
окружности}; интервал интегрирования
[0.5, 1]; результат s1.
{верхняя
полуокружность правой центральной
окружности}; интервал интегрирования
[0.5, 1]; результат s1.
 {верхняя
полуокружность центральной окружности};
интервал интегрирования [0.5,
/2];
результат s2.
{верхняя
полуокружность центральной окружности};
интервал интегрирования [0.5,
/2];
результат s2.
 {нижняя
полуокружность центральной верхней
окружности}; интервал интегрирования
[
/2,
1]; результат s3.
{нижняя
полуокружность центральной верхней
окружности}; интервал интегрирования
[
/2,
1]; результат s3.
Площадь области M2=s1-s2-s3.
- условие 3 (принадлежность области М3):
(x-1)2+y2<1 {внутри правой окружности}
(x-1)2+(y-1)2>1 {вне правой верхней окружности}
y>0 {выше оси x}
x>1 {правее линии x=1}
Аналитическое выражение определения площади области М3:
четверть площади круга (πr2/4) - (площадь сектора 1200 (πr2/3) – площадь треугольника ( /2×0.5)) = π/4 – π/3+ /2×0.5 = /4 - π/12 ≈ 0.1712
Аналитический вид функций, подлежащих интегрированию:
 {нижняя
полуокружность правой верхней окружности};
интервал интегрирования [1, 1+
/2];
результат s1.
{нижняя
полуокружность правой верхней окружности};
интервал интегрирования [1, 1+
/2];
результат s1.
{верхняя полуокружность правой центральной окружности}; интервал интегрирования [1+ /2, 2]; результат s2.
M3=s1+s2
- условие 4 (принадлежность области М4):
(x+1)2+(y+1)2<1 {внутри левой нижней окружности}
(x+1)2+y2>1 {вне левой окружности}
x<-1 {левее линии x=-1}
Аналитическое выражение определения площади области М4:
четверть площади круга (πr2/4) + четверть площади круга (πr2/4) - (площадь сектора 1200 (πr2/3) – площадь треугольника ( /2×0.5)) = π/4+π/4 – π/3+ /2×0.5 = π/6 + /4 ≈ 0.9566
Аналитический вид функций, подлежащих интегрированию:
 {нижняя
полуокружность левой нижней окружности};
интервал интегрирования [-2, -1]; результат
s1.
{нижняя
полуокружность левой нижней окружности};
интервал интегрирования [-2, -1]; результат
s1.
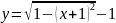 {верхняя
полуокружность левой нижней окружности};
интервал интегрирования [-2, -1 -
/2];
результат s2.
{верхняя
полуокружность левой нижней окружности};
интервал интегрирования [-2, -1 -
/2];
результат s2.
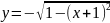 {нижняя
полуокружность левой центральной
окружности}; интервал интегрирования
[-1 -
/2,
-1]; результат s3.
{нижняя
полуокружность левой центральной
окружности}; интервал интегрирования
[-1 -
/2,
-1]; результат s3.
M4=s1-s2-s3
- условие 5 (принадлежность области М5):
(x-1)2+(y+1)2<1 {внутри правой нижней окружности}
(x-1)2+y2>1 {вне правой окружности}
Аналитическое выражение определения площади области М5:
половина площади круга (πr2/2) + 2*(четверть площади круга (πr2/4) - (площадь сектора 1200 (πr2/3) – площадь треугольника ( /2×0.5))) = π/2+2*(π/4 – π/3+ /2×0.5) = π/3 + /2 ≈ 1.9132
Аналитический вид функций, подлежащих интегрированию:
 {нижняя
полуокружность правой нижней окружности};
интервал интегрирования [0, 2]; результат
s1.
{нижняя
полуокружность правой нижней окружности};
интервал интегрирования [0, 2]; результат
s1.
 {нижняя
полуокружность правой центральной
окружности}; интервал интегрирования
[1-
/2,
1+
/2];
результат s2.
{нижняя
полуокружность правой центральной
окружности}; интервал интегрирования
[1-
/2,
1+
/2];
результат s2.
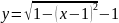 {верхняя
полуокружность правой нижней окружности};
интервал интегрирования [0, 1-
/2];
результат s3.
{верхняя
полуокружность правой нижней окружности};
интервал интегрирования [0, 1-
/2];
результат s3.
{верхняя полуокружность правой нижней окружности}; интервал интегрирования [1- /2, 2]; результат s4.
M5=s1-s2-s3-s4
Текст программы
/*Определение области на плоскости, в которую попадает точка,
и площади этой области аналитическим и программным способом
методом криволинейных трапеций.
Рекурсия. Передача имен функций в качестве параметров.*/
#define _USE_MATH_DEFINES //для определения значения M_PI
#include<iostream>
#include<math.h>
#include<locale.h>
using namespace std;
typedef double(*Tfun)(double);
double integral(double, double, int, double, Tfun, double);
double fun1(double x);
double fun2(double x);
double fun3(double x);
double fun4(double x);
double fun5(double x);
double fun6(double x);
double fun7(double x);
double fun8(double x);
double fun9(double x);
double fun10(double x);
double fun11(double x);
double fun12(double x);
double fun13(double x);
double fun14(double x);
int main()
{
int i = 0, //номер области
n = 10; //начальное число разбиений
double x, y, //координаты точки
s1, s2, s3, s4, s5; //площади областей
double eps = .0001, //точность вычисления
s = 0; //вычисленная площадь области
setlocale(LC_ALL, "Russian");
cout << '\n' << "Введите координаты точки: x,y ";
cin >> x >> y;
if ((x + 1) * (x + 1) + (y - 1) * (y - 1) < 1 &&
x * x + (y - 1) * (y - 1) < 1 &&
(x + 1) * (x + 1) + y * y > 1)
{
cout << "Точка в области M1. "; i = 1;
}
else if (x * x + (y - 1) * (y - 1) < 1 &&
(x - 1) * (x - 1) + y * y < 1 &&
x * x + y * y > 1)
{
cout << "Точка в области М2. "; i = 2;
}
else if ((x - 1) * (x - 1) + y * y < 1 &&
(x - 1) * (x - 1) + (y - 1) * (y - 1) > 1 &&
y > 0 && x > 1)
{
cout << "Точка в области М3. "; i = 3;
}
else if ((x + 1) * (x + 1) + (y + 1) * (y + 1) < 1 &&
(x + 1) * (x + 1) + y * y > 1 &&
x < -1)
{
cout << "Точка в области М4. "; i = 4;
}
else if ((x - 1) * (x - 1) + (y + 1) * (y + 1) < 1 &&
(x - 1) * (x - 1) + y * y > 1)
{
cout << "Точка в области М5. "; i = 5;
}
else cout << "Точка вне выделенных областей";
cout.precision(4); //число знаков после дес. точки
switch (i)
{
case 1: cout << "Formula: S1 = " << (s1 = M_PI / 4) << endl;
cout << "Integral:S1 = " << (s1 = integral(-0.5, 0, n, eps, fun1, s) + integral(-1, -0.5, n, eps, fun2, s)
- integral(-1, (sqrt(3) / 2) - 1, n, eps, fun3, s) - integral((sqrt(3) / 2) - 1, 0, n, eps, fun4, s));
break;
case 2: cout << "Formula: S2 = " << (s2 = sqrt(3) / 2 + M_PI / 3 - M_PI / 4 - 1) << endl;
cout << "Integral:S2 = " << (s2 = integral(0.5, 1, n, eps, fun5, s) - integral(0.5, sqrt(3) / 2, n, eps, fun6, s)
- integral(sqrt(3) / 2, 1, n, eps, fun7, s));
break;
case 3: cout << "Formula: S3 = " << (s3 = sqrt(3) / 4 - M_PI / 12) << endl;
cout << "Integral:S3 = " << (s3 = integral(1, 1 + sqrt(3) / 2, n, eps, fun8, s)
+ integral(1 + sqrt(3) / 2, 2, n, eps, fun5, s));
break;
case 4: cout << "Formula: S4 = " << (s4 = M_PI / 6 + sqrt(3) / 4) << endl;
cout << "Integral:S4 = " << (s4 = fabs(integral(-2, -1, n, eps, fun9, s))
- fabs(integral(-2, -1 - sqrt(3) / 2, n, eps, fun10, s))
- fabs(integral(-1 - sqrt(3) / 2, -1, n, eps, fun11, s)));
break;
case 5: cout << "Formula: S5 = " << (s5 = M_PI / 3 + sqrt(3) / 2) << endl;
cout << "Integral:S5 = " << (s5 = fabs(integral(0, 2, n, eps, fun12, s)) - fabs(integral(1 - sqrt(3) / 2, 1 + sqrt(3) / 2, n, eps, fun13, s))
- fabs(integral(0, 1 - sqrt(3) / 2, n, eps, fun14, s)) - fabs(integral(1 + sqrt(3) / 2, 2, n, eps, fun14, s)));
}
cout << "\n Повторить-1, Выход-2: ";
cin >> i;
if (i == 1) main();
return 0;
}
//нахождение определенного интеграла методом криволинейных трапеций
double integral(double a, double b, int n, double eps, Tfun fun, double s1)
{
double x,
h,
s = 0;
int i;
h = (b - a) / n;
for (i = 0; i < n; i++)
{
x = a + i * h + h / 2;
s += fun(x);
}
s *= h;
if (fabs(s - s1) > eps)
s = integral(a, b, 2 * n, eps, fun, s);
return s;
}
/*описание вида интегрируемой функции №1 для линии: (x+1)^2+(y-1)^2=1 (верхняя полуокружность)*/
double fun1(double x)
{
return(sqrt(1 - (x + 1) * (x + 1)) + 1);
}
/*описание вида интегрируемой функции №2 для линии: x^2+(y-1)^2=1 (верхняя полуокружность)*/
double fun2(double x)
{
return(sqrt(1 - x * x) + 1);
}
/*описание вида интегрируемой функции №3 для линии: (x+1)^2+y^2=1 (верхняя полуокружность)*/
double fun3(double x)
{
return(sqrt(1 - (x + 1) * (x + 1)));
}
/*описание вида интегрируемой функции №4 для линии: (x+1)^2+(y-1)^2=1 (нижняя полуокружность)*/
double fun4(double x)
{
return(-sqrt(1 - (x + 1) * (x + 1)) + 1);
}
/*описание вида интегрируемой функции №5 для линии: (x-1)^2+y^2=1 (верхняя полуокружность)*/
double fun5(double x)
{
return(sqrt(1 - (x - 1) * (x - 1)));
}
/*описание вида интегрируемой функции №6 для линии: x^2+(y-1)^2=1 (верхняя полуокружность)*/
double fun6(double x)
{
return(sqrt(1 - x * x));
}
//описание вида интегрируемой функции №7 для линии: x^2+(y-1)^2=1 (нижняя полуокружность)
double fun7(double x)
{
return(-sqrt(1 - x * x) + 1);
}
//описание вида интегрируемой функции №8 для линии: (x-1)^2+(y-1)^2=1 (нижняя полуокружность)
double fun8(double x)
{
return(-sqrt(1 - (x - 1) * (x - 1)) + 1);
}
/*описание вида интегрируемой функции №9 для линии: (x+1)^2+(y+1)^2=1 (нижняя полуокружность)*/
double fun9(double x)
{
return(-sqrt(1 - (x + 1) * (x + 1)) - 1);
}
/*описание вида интегрируемой функции №10 для линии: (x+1)^2+(y+1)^2=1 (верхняя полуокружность)*/
double fun10(double x)
{
return(sqrt(1 - (x + 1) * (x + 1)) - 1);
}
/*описание вида интегрируемой функции №11 для линии: (x+1)^2+y^2=1 (нижняя полуокружность)*/
double fun11(double x)
{
return(-sqrt(1 - (x + 1) * (x + 1)));
}
/*описание вида интегрируемой функции №12 для линии: (x-1)^2+(y+1)^2=1 (нижняя полуокружность)*/
double fun12(double x)
{
return(-sqrt(1 - (x - 1) * (x - 1)) - 1);
}
/*описание вида интегрируемой функции №13 для линии: (x-1)^2+y^2=1 (нижняя полуокружность)*/
double fun13(double x)
{
return(-sqrt(1 - (x - 1) * (x - 1)));
}
/*описание вида интегрируемой функции №14 для линии: (x-1)^2+(y+1)^2=1 (верхняя полуокружность)*/
double fun14(double x)
{
return(sqrt(1 - (x - 1) * (x - 1)) - 1);
}
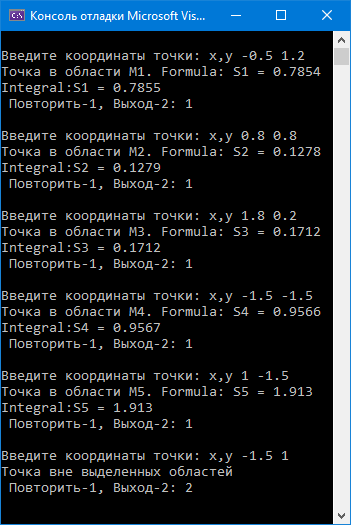
Скриншот результатов выполнения программы