
x=a c вероятностью T1/T, x=b c вероятностью T2/T
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
||
m |
|
xW (x)dx |
|
|
T |
(x b)dx |
|
|
T |
(x |
a)dx |
|
f (x) (x a)dx f (a) |
|
||||||||||||||
|
|
x |
2 |
|
x |
1 |
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
b |
T1 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
T1 |
|
|
|
|
|
|
|
|
|
|
|
|||
m2 x2W (x)dx b2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
T |
T |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 m m2 |
b2 |
T2 |
a2 |
T1 |
( |
T2 |
b |
T1 |
a)2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
1 |
|
|
T |
|
|
T T |
|
|
|
T |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11.7.Нелинейные безынерционные преобразования случайного процесса.
Нелинейное преобразование:
y(t)=f[x(t)] – называется безынерционным, если y(tk) в момент времени tk зависит только от x(tk).
ФПВ для процесса y на выходе:
W ( y) W (x) |
|
dx |
|
|
W (x) |
||||
dy |
|
||||||||
|
|
|
|
|
|
dy |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
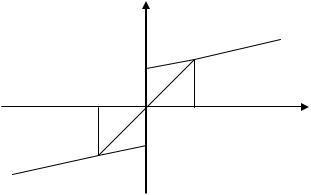
Пусть характеристика нелинейного элемента может быть аппроксимирована линейно-ломаными.
y
Рис.11.14
|
b |
|
-a |
a |
x |
|
-b |
|
21

nx b, x a y kx, kx a
nx b, x a
Это нелинейное устройство называется ограничителем.
Пусть на входе ограничителя действует нормальный случайный процесс с нулевым средним m1x=0.
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x 2 |
|
|
||||
W (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e 2 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ФПВ процесса x нарисована на рис.11.15 (верхний рисунок). |
||||||||||||||||||||||||||
Рассчитаем ФПВ процесса y: |
|
|||||||||||||||||||||||||
1. Пусть |
|
x |
|
|
a |
|
|
у=kx (k>1) |
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
W ( y) |
W (x |
) |
|
|
W (x) |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
dy |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим в W(x) вместо x выражение y/k, тогда |
||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
e |
|
|
|
y2 |
|
|
||||||||||
W ( y) |
|
|
|
|
|
|
|
2k 2 2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
На интервале |
|
y |
|
ka ФПВ для у будет |
нормальной, со средним |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||
значением m1y=0, но дисперсия y, т.е. 2y k 2 2 |
2 (т.к. k 1) . |
|||||||||||||||||||||||||
22
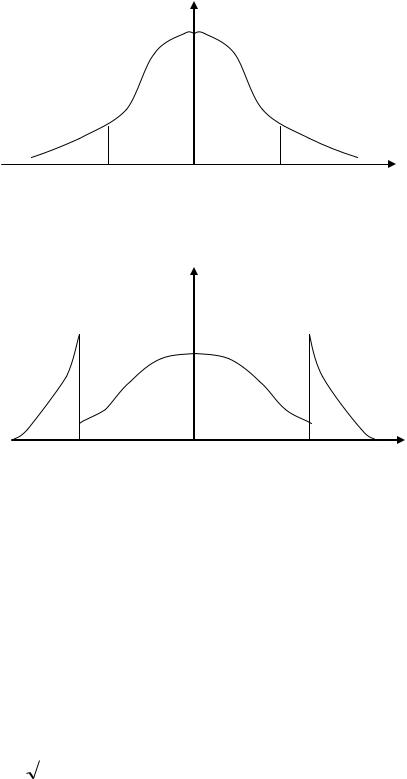
W(x)
x
-a |
a |
W(y)
Рис.11.15.
|
|
|
|
|
|
|
|
|
-ka |
|
|
0 |
ka |
y |
||||||
2. Пусть: x a |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
y ka |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y nx b |
|
|
|
|
|
|
|
|
|
|||||||||
W ( y) |
W (x |
) |
|
|
W (x) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dy |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражаем x через у, т.е. x |
|
y b |
|
|
|
|||||||||||||||
|
n |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
e |
( y b)2 |
|
|
|
|
|
|
|
W ( y) |
|
|
|
|
|
|
|
|
2n2 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Это нормальная |
|
ФПВ |
со средним |
значением |
b и дисперсией |
|||||||||||||||
n2 2 2 ,(n 1) |
|
|
|
|
|
|
|
|
|
|||||||||||
23
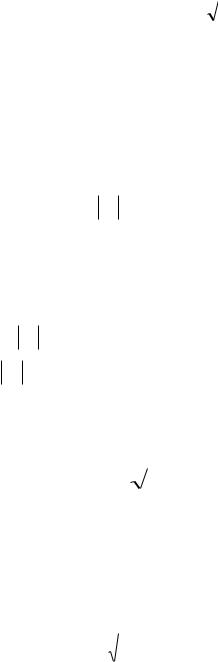
3.Пусть:
x a y ka
y nx b
|
W (x |
) |
|
W (x) |
|
1 |
|
|
e |
( y b)2 |
||
W ( y) |
|
|
|
|
2n2 2 |
|||||||
|
|
|
|
|
|
|||||||
|
dy |
|
|
n |
n |
2 |
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
Это нормальная ФПВ, m1= -b и дисперсия n2 2 . ФПВ процесса y дана на рис.11.15 (нижний рисунок).
11.8.ФПВ процесса на выходе идеализированного ограничителя.
Такой ограничитель имеет горизонтальные участки насыщения.
kx, x a
y ka, x a
ka, x a
1. x a, y kx y ka
|
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 k 2 2 |
|
|
|
|
|
|
|||
W ( y) |
e |
|
, |
|
y |
|
ka |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
k |
|
2 |
||||||||
|
|
|
|
|
|
|
|
|||
2.x a; y ka
|
|
|
(y b) |
2 |
|
|
|
при..n , дисперсия |
|
|
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
W(y) lim e |
2n |
2σ |
2 |
|
|
|
" уши " сжимаются и к функции |
P(x a) ( y ka) |
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
( y ka) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
nσ |
|
2π |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
n ,b ka |
|
|
|
|
||||||||
24
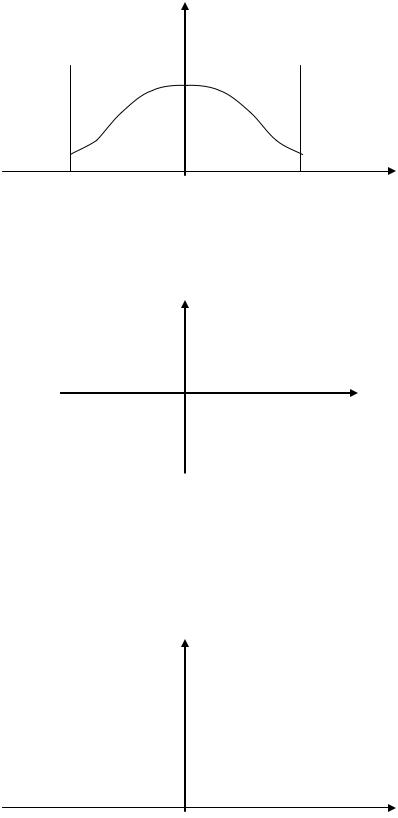
3.x a; y ka
W ( y) P(x a) ( y ka)
W(y)
P(x<-a) (y+ka) |
P(x>a) (y-ka) |
Рис.11.16.
-ka |
0 |
ka |
y |
11.9.ФПВ процесса на выходе идеального ограничителя.
Характеристика идеального ограничителя показана на рис.11.17. y
|
|
|
ka |
|
Рис.11.17. |
|
|
|
|
||
|
|
|
|
|
x |
|
|
|
|
-ka |
|
|
|
|
|
|
|
Процесс |
на выходе |
идеального ограничителя |
y - имеет только два |
||
значения : |
ка и –ка. |
Т.к. вероятность положительных и отрицательных |
|||
значений х |
равна 0.5, то вероятность того, что y принимает значения +ka |
||||
или -ka также равна 0.5. Поэтому, выполняя расчеты, как в предыдущем случае, получим, что ФПВ процесса y вырождается в две дельта-функции в точках y=-ka и y=ka (рис.11.18):
|
|
W(y) |
|
|
|
0,5 (y+ka) |
|
0,5 (y-ka) |
|
||
|
|
|
|
|
Рис.11.18. |
|
|
|
|
|
|
-ka |
0 |
ka |
y |
||
25
11.10.Линейные (инерционные) преобразования случайного процесса.
Линейная инерционная система – это линейный фильтр.
В этом случае процесс на выходе системы у(t1) зависит от входного процесса x не только в момент времени t1, но и от значений x в предшествующие и последующие моменты времени:
y(t) x( )g(t )d
|
|
|
y(t) выходной |
случайный |
процесс |
x( ) входной |
случайный |
процесс |
g(t ) импульсная реакция линейной цепи
1.Если процесс на входе ЛЭЦ нормальный, то у тоже нормальный случайный процесс, но его числовые характеристики отличаются от числовых характеристик процесса x и вычисляются следующим образом:
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
m1y |
y(t) |
|
x( ) |
g(t )d m2 y |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m2 y y(t2 ) |
x( )g(t )d |
x(v)g(t v)dv |
|
g(t )g(t v)d dv |
||||||||
x( )x(v) |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
2. Если процесс на входе ЛЭЦ не нормальный, но ширина его спектра значительно больше полосы пропускания линейной цепи x Плэц , то
процесс на выходе ЛЭЦ имеет тенденцию к нормализации.
12.Функция корреляции.
Функция корреляции характеризует степень статистической зависимости двух значений случайного процесса, разделенных интервалом времени .
Общее определение – функция корреляции случайного процесса B(t1,t2) это второй смешанный момент распределения случайного процесса:
B(t1 , t2 ) x(t1 ) x(t2 )W (x(t1 ); x(t2 ))dx(t1 )dx(t2 )
(12.1)
Для эргодического стационарного случайного процесса с нулеым средним функция корреляции зависит только от разности =(t2-t1) и определяется выражением:
26
|
|
|
T |
|
|
|||
|
1 |
2 |
|
|
|
|||
B( ) lim |
|
x(t) x(t )dt |
(12.2) |
|||||
|
||||||||
T T |
|
T |
|
|||||
|
|
2 |
|
|
||||
|
|
|
|
|
|
|||
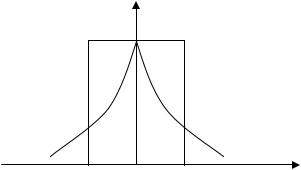
Стандартный вид функции корреляции.
В( )
В(0)
Рис.12.1.
- к |
0 |
к |
|
1.В( ) - четная; В( ) = В(- )
2.В(0) - max; В(0) = 2 (средняя мощность переменной составляющей, т.е. дисперсия случайного процесса).
3. |
|
lim |
B( ) 0 |
|
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
B( )d |
|
|
||
4. k |
|
0 |
|
|
интервал корреляции |
случайного процесса, |
|
|
B(0) |
||||||
|
|
|
|
|
|
||
характеризует ширину графика функции корреляции: |
|||||||
Если | | к - то значения СП коррелированны, |
|
||||||
|
Если |
| | > к - то значения СП не коррелированны. |
|||||
|
5. R( ) = В( ) / В(0) - коэффициент корреляции, |
R( ) 1. |
|||||
13.Энергетический спектр.
Энергетическим спектром G( ) называется зависимость энергии составляющих случайного процесса от частоты.Стандартный вид энергетического спектра:
27
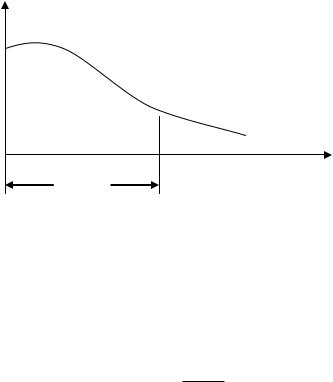
G( )
Рис.13.1.
0 |
|
Пэ
Энергетический спектр показывает, какая энергия процесса заключена в единичной полосе частот, т.е. это энергия процесса, приходящаяся на 1Гц или на 1 рад/с. Размерность G( ) --- В2/Гц или В2/ рад*Гц
Пэ - ширина энергетического спектра,т.е. полоса частот, в пределах которой заключено порядка 95 - 99,9 энергии всего процесса. Она обратно пропорциональна интервалу корреляции
const
ПЭ k ;
const 3 6- зависит от ограничений накладываемых на сигнал .
14.Соотношение Винера - Хинчина и его применение к решению задач
Это соотношение связывает функцию корреляции и энергетический спектр случайного процесса. В теории случайных процессов это соотношение аналогично преобразованию Фурье для детерминированных процессов:
|
|
|
|
G( ) 4 B( ) cos( )d |
|
||
|
0 |
|
(14.1) |
|
1 |
|
|
|
|
||
B( ) |
G( ) cos( )d |
|
|
2 |
|
||
|
0 |
|
|
|
|
|
|
Коэффициенты могут быть и другими.
В теории связи, в качестве модели помехи, часто используется случайный процесс, называемый аддитивный белый гауссовский шум (АБГШ). Белым шумом (АБГШ) называется абсолютно случайный (дикий) процесс, энергетический спектр которого бесконечен и равномерен.
28
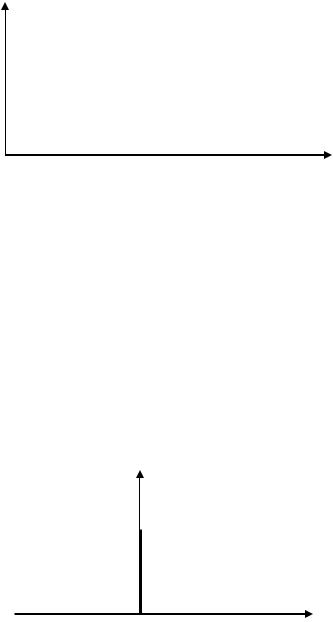
G( )
G0 |
|
Рис.14.1. |
0
G( ) = G0 при 0
G0 - спектральная плотность белого шума (мощность, приходящаяся на 1Гц или 1рад/с) .
Мощность белого шума в полосе частот ( в рад/с ) :
P = G0*
Пример белого шума - это тепловой шум. Функция корреляции белого шума вычисляется в соответствии с преобразованием Винера-Хинчина:
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
cos(w )dw |
|
||
B( ) |
G(w) cos(w )dw |
G0 cos(w )dw G0 |
0 |
|
|
G0 ( ) |
||
|
|
|
|
|||||
2 |
2 |
|
2 |
|||||
|
|
0 |
|
0 |
|
|
||
( )
Функция корреляции белого шума имеет следующий вид:
В( )
G0 ( )
Рис.14.2.
0 |
|
Рассмотрим прохождение белого шума через полосовой фильтр. На входе идеального полосового фильтра с АЧХ равной :
|
|
|
0 |
|
|
Пэ |
|
|
|
|
|||||
k0 |
при |
|
|
|
|||
|
2 |
||||||
|
|
|
|||||
k( ) |
|
|
|
|
|
|
Пэ |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
0 |
при |
|
|
|
|||
|
|
|
|
|
|
|
2 |
29
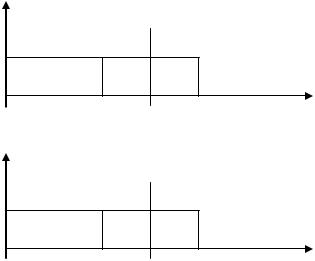
действует нормальный белый шум со спектральной плотностью G0. Определим функцию корреляции и ФПВ процесса y на выходе фильтра;
т.е. В( )вых и W(y) .
Спектр белого шума на входе фильтра показан на рис.14.1.
АЧХ полосового фильтра показана на рис. 14.3, а спектр процесса на выходе полосового фильтра изображен на рис.14.4.
К( )
К0
0 ( 0 -Пэ/2) |
0 |
( 0 +Пэ/2) |
|
Рис.14.3
G( )вых
G0К02
0 ( 0 -Пэ/2) |
0 |
( 0 +Пэ/2) |
|
|
|
|
Рис.14.4. |
Спектральная плотность белого шума на выходе ПФ: G( )вых = G0К02, т.к. АЧХ показывает во сколько раз изменится амплитуда напряжения, следовательно, энергия изменится в К02 раз. В соответствии с соотношением Винера - Хинчина, зная G( )вых найдем В( )вых. :
|
|
|
|
|
|
|
0 |
|
П э |
|
|
|
0 |
|
П э |
|
|
|
|
|
|
||||
|
|
|
|
1 |
2 |
|
|
1 |
2 |
|
|
1 |
|
|
э |
|
|||||||||
B( )вых |
|
|
|
|
G( )вых cos d |
|
G0 K0 |
2 cos d |
G0 K0 |
2 2sin |
cos 0 |
||||||||||||||
2 |
2 |
2 |
2 |
||||||||||||||||||||||
|
|
|
|
П э |
|
|
|
П э |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
K 2 |
G |
|
|
sin |
|
э |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
э |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
э |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
