Добавил:

Morze Developer Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Общая теория связи

Файл:

Лекции / Лекция 7-05

.pdf

Скачиваний:

Добавлен:

04.05.2022

Размер:

1.07 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

11. Случайные процессы.

11.1.Характеристики случайных процессов

Процессы, рассматриваемые в теории связи, могут быть детерминированными или случайными.

Детерминированные процессы - это процессы, течение которых во времени известно заранее и абсолютно точно.

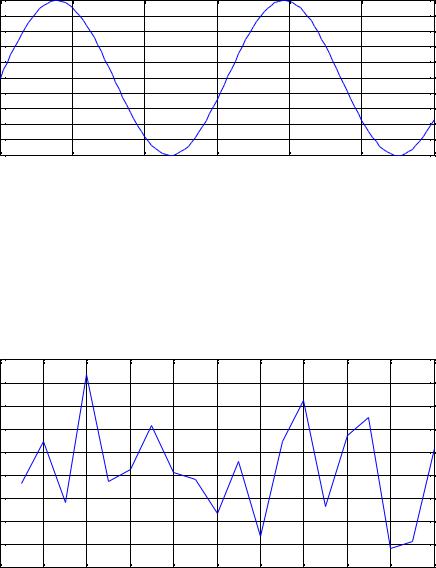
Например, гармонический сигнал U(t) = Umcos( 0t+ 0), где Um,, 0, 0 - заданы.

1
	U(t)
0.8
0.6
0.4
0.2
						t
0
-0.2
-0.4
-0.6
-0.8
-1 0	2	4	6	8	10	12

Его значения можно абсолютно точно предсказать заранее. Это простейшая модель информационного сигнала, но она оказывается очень не точной для современных систем связи, дает большие погрешности в расчетах. Поэтому вводится новая модель, более сложная - случайные процессы (СП). Случайные процессы таковы, что их течение во времени заранее точно предсказать невозможно.

Пример СП - тепловой шум x(t) – случайное напряжение на поверхности, например, руки человека из-за движения свободных зарядов.

2.5
	x(t)
2
1.5
1
0.5
										t
0
-0.5
-1
-1.5
-2 0	2	4	6	8	10	12	14	16	18	20

Процесс случайный, т.к. мы не знаем с какой скоростью и куда движется каждый заряд. СП описывается своими реализациями, т.е. конкретными образцами.

Совокупность реализаций образует ансамбль (полная, но очень сложная характеристика СП).

Функция распределения вероятностей СП (ФРВ).

Функция распределения вероятностей обозначается F(x), характеризует вероятность того, что случайный процесс в некоторый момент времени t1 принимает значение меньшее x1 . Полное обозначение одномерной ФРВ

F(x1 ,t1 ) = P(x<x1 , t=t1 )

Двумерная ФРВ.

F2 (x1 t1 ,x2t2) = P (x<x1, t=t1 ,x<x2;t=t2)

Наиболее полная характеристика СП n- мерная ФРВ:

Fn (x1t1...xntn) = P (x<x1;t<t1; ... x<xn;t=tn)t

Функция плотности вероятностей случайного процесса ( ФПВ)

В простейшем случае одномерная ФПВ равна:

	W(x1t1 ) lim	P(x1 x x1 x;t t1 )
	W(x1t1 ) lim	x
	x 0	x

Одномерная ФПВ равна пределу отношения вероятности попадания случайного процесса в интервал от x1 до х1+ х, при t= t1, к х при х стремящемся к нулю.

Наиболее полной характеристикой является n - мерная ФПВ.

ФРВ и ФПВ связаны друг с другом . ФПВ - это первая производная ФРВ по х1 :

W (x1 , t1 ) F(x1 , t1 )

Соответственно, ФРВ равна интегралу от - до х1 от ФПВ:.

F(x1t1) = W (x1t1 )dx1

Условие нормировки :

W(x1t1 )dx1 1

Числовые характеристики случайного процесса .

Среднее значение ( математическое ожидание или первый начальный момент)

m1 = x = xW (x, t )dx

Физический смысл m1 - это постоянная составляющая случайного процесса.

2.Второй начальный момент.

m2 = x2 = x2W (x,t)dx

Физический смысл m2 - это полная средняя мощность случайного процесса на единичном сопротивлении.

3.Дисперсия ( второй центральный момент )

2 = М2 = (x m1 )2 (x m1 )2W (x,t)dx

Физический смысл 2 - это средняя мощность переменной составляющей случайного процесса на единичном сопротивлении.

Числовые характеристики связаны между собой:

2 = m2 - m12

Стационарность.

1.Нестационарный случайный процесс - ФПВ и ФРВ зависят от начала отсчета времени.

2.Стационарный в узком смысле - ФПВ и ФРВ не зависят от начала отсчета времени.

3.Стационарный в широком смысле - одно- и двумерные ФПВ и ФРВ не зависят от начала отсчета времени.

Для стационарного случайного процесса m1, m2, 2 - не зависят от времени.

Рассмотрим тепловой шум на выходе включенного усилителя:

x(t)

Рис.11.1.

нестационарный Стационарный

После включения усилитель прогревается и шум на его выходе - нестационарный. После "прогрева" шум будет стационарным процессом.

Эргодичность.

Случайный процесс называется эргодическим, если для него усреднение по времени одной реализации и усреднение по множеству реализаций дает один и тот же результат. Это свойство имеет большое значение на практике, т.к. усреднение по времени одной реализации технически реализовать проще, но оно не всегда дает истинный результат. Поэтому доказательство эргодичности процесса позволяет существенно упростить нахождение его характеристик.

11.2.Нормальный случайный процесс( гауссов процесс).

Процесс называется нормальным или гауссовым, если его одномерная ФПВ имеет вид:

				( x m ) 2
	1			1
W (x)			e	2 2
				2 2

		2

0.4
				W(x)
0.35
0.3
				M2=1
0.25
0.2
0.15
0.1
					M2=4
0.05
						x
0
-6	-4	-2	0	2	4	6
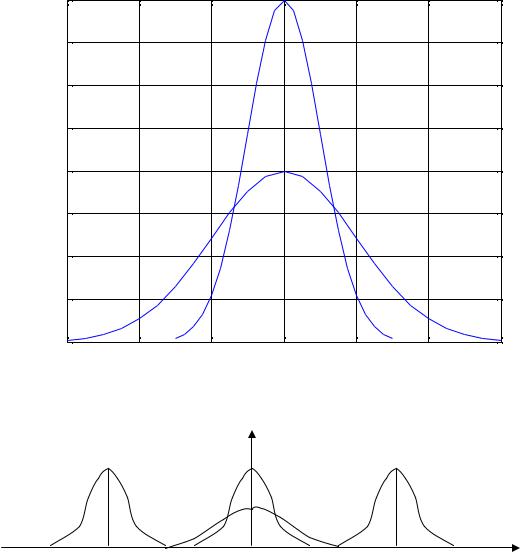
Графики нормальной ФПВ построены на рис. 11.2.:

	W(x)
1	1	1
m1<0	m1=0	m1>0 Рис.11.2.
	2> 1
		х

m1 - среднее значение случайного процесса .2 - дисперсия случайного процесса .

Свойства нормального случайного процесса .

1.W(x) 0

2.Нормальная ФПВ симметрична относительно x = m1

3.W(x) - max при х = m1

4.Площадь под кривой W(x) равна 1.

5.При изменении m1 форма кривой не меняется, но кривая смещается вдоль оси х.

6.Чем больше дисперсия 2, тем кривая ниже и шире.

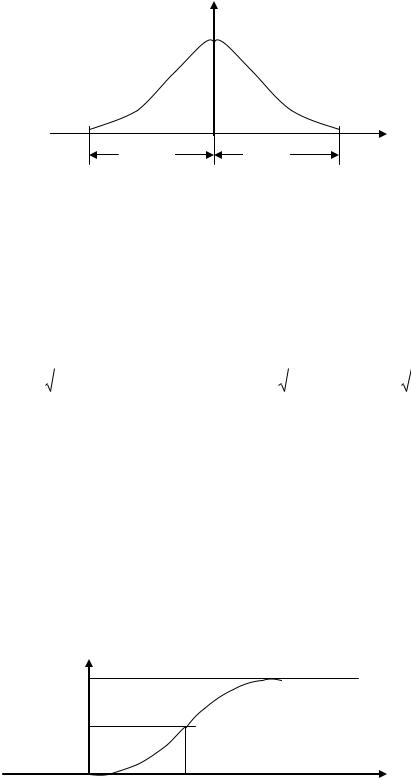
7.С вероятностью близкой к 1 (р 0,997) мгновенные значения нормального случайного процесса лежат в пределах:

m1 - 3 < x < m1+3

W(x)

Рис.11.3.

Если известны дисперсия и среднее значение нормального процесса, то рабочий участок ВАХ должен иметь протяженность m1 3 .

8. ФРВ для нормального случайного процесса

x m

x m1

(x m1 )2

y 2

F(x)

2 dy

= F(

x m1

)

- табулированная функция (интеграл вероятности Лапласа)

F (0) =

0.5

F (-x) = 1- F(x)

F (3.9)

= 0.99995

F (- )

= 0; F( )

ФРВ для нормального процесса имеет вид:

F (x)
1
0.5		Рис.11.4.
0	m1	x

11.3.ФПВ и ФРВ для гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс в виде гармонического колебания со случайной начальной фазой:

X(t) = Asin ( wt + )

- случайная величина, равномерно распределенная на интервале , т.е. ФПВ мгновенных значений фазы , показанная на рис.11.5 равна:

W( ) = 21π ; |x| (ПЛОЩАДЬ ПОД КРИВОЙ W(x) РАВНА 1)

W( )

			1/2
													Рис.11.5.
													Рис.11.5.
		-		0
Вычислим среднее значение :
									1		1
m1	xW (x)dx								1	d	1	d 0
m1	xW (x)dx								2	d	2	d 0
									2		2

Вычислим дисперсию:

2		2			2		1			1 3		3		2
		(x m1 ) W (x)dx						d
		(x m1 ) W (x)dx				2		d		2 3		3		3
						2				2 3		3		3

ФПВ мгновенных значений x гармонического колебания со случайной фазой, изображенная на рис. 11.6, имеет вид:

0, \| x \| A;
	1
W (x)	1			, \| x \| A;


	2	x	2
	A	x

W(x)

Рис.11.6.

-A

Чем больше А, тем кривая ниже и шире. Заштрихованная площадь равна единице. Это площадь под кривой W(x) (условие нормировки)..

ФРВ мгновенных значений для гармонического колебания со случайной фазой ( рис. 11.7):

x(t) = Asin ( t + )

0,\| x \| A;
	1	1		x
	1	1		x
F (x)			arcsin		, \| x \| A
F (x)	2		arcsin	A	, \| x \| A
	2			A
1, x A

F(x)

0.5

Рис.11.7.

-A

11.4. ФПВ для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс z(t), равный:

Z(t) = x(t) + Asin (wt+ )

где x(t) - нормальный случайный процесс;

Asin (wt+ ) - гармоническое колебание со случайной начальной фазой.

W(z) в этом случае находится сверткой.

	1	1		( z x)2
W (z)	1	1		e 2 2 dx

			2
	A2 x 2		2

Вид ФПВ, т.е. W(z) зависит от параметра:

h2	A2
h2	2 2
	2 2
		W(z)
		h2=0	h2=
			h2= 6
			Рис.10.8.
	0		z
h2 = 0 - нормальный случайный процесс			(чистый шум).
h2 - одно гармоническое колебание.

ЛАБОРАТОРНАЯ РАБОТА №12

«ВЕРОЯТНОСТНЫЕ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ»

1. Цель работы: Теоретическое и экспериментальное изучение методов измерения одномерных функций плотности вероятностей (ФПВ), функций распределения вероятностей (ФРВ) и числовых характеристик эргодических, стационарных случайных процессов.

2.ДОМАШНЕЕ ЗАДАНИЕ.

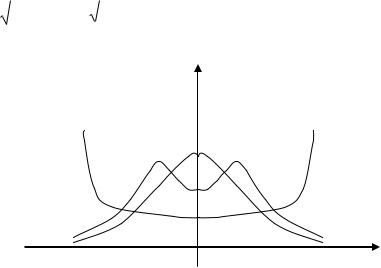
1.Рассчитать и построить ФПВ и ФРВ гармонического колебания со случайной начальной фазой для двух значений А:

x(t)=A cos( t + ); A – амплитуда гармонического колебания;

- частота гармонического колебания;- случайная фаза, равномерно распределенная на интервале: -

< < .

Определить дисперсию x(t) путем усреднения по времени одной реализации и путем усреднения по множеству реализаций.

2.Рассчитать и построить ФПВ и ФРВ эргодического, стационарного

нормального случайного процесса со средним значением m1=0 для двух значений дисперсии 2.

3.Рассчитать и построить ФПВ случайного процесса, образованного

суммой гармонического колебания с амплитудой А1 и нормального случайного процесса со средним значением m1=0 и дисперсией 12.

4.Рассчитать и построить ФПВ и ФРВ дискретного случайного

процесса y(t), заданного таблицей. Определить его среднее значение m1 , полную мощность m2 и дисперсию 2 .

Вариант №31. Исходные данные к расчету:
А1 =1в ;	А2 =2в ;		12 =1в2 ;		22 =4в2 ;
Интервал		0-Т		Т-2Т		2Т-3Т	3Т-4Т	4Т-5Т
времени
Значение		1		1		0	-1	1
у(t)

1.Рассмотрим случайный процесс в виде гармонического колебания со случайной начальной фазой:

x(t)=A cos( t + );

- случайная величина, равномерно распределенная на интервале , т.е. ФПВ мгновенных значений фазы , показанная на рисунке равна:

W( )	1	; \| \|
W( )	2	; \| \|
	2
			W( )
			1/2


		-	0

ФПВ мгновенных значений x гармонического колебания со случайной фазой имеет вид:

0,		\| x \| A;
		1
W (x)		1					, \| x \| A;


		2		x		2
			A	x

х	-0.9					-0.6			-0.3		0		0.3		0.6		0.9
A=1
W(x)	0.7306					0.3981			0.3338		0.3185		0.3338		0.3981		0.7306

x	-1.8				-1.2			-0.6		0		0.6		1.2		1.8
A=2

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке Лекции

#
04.05.2022837.45 Кб85Лекции.pdf
#
04.05.20221.49 Mб33Лекция 23-4.pdf
#
04.05.2022472.09 Кб33Лекция 26-3.pdf
#
04.05.20221.07 Mб39Лекция 7-05.pdf
#
04.05.2022794.5 Кб28Лекция 9-4.pdf