Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Теоретические основы электротехники

Файл:

Задания и методические указания к выполнению контрольных работ по дисциплине «Теоретические основы электротехники». Попова Т.В., Щербаков А.М

.pdf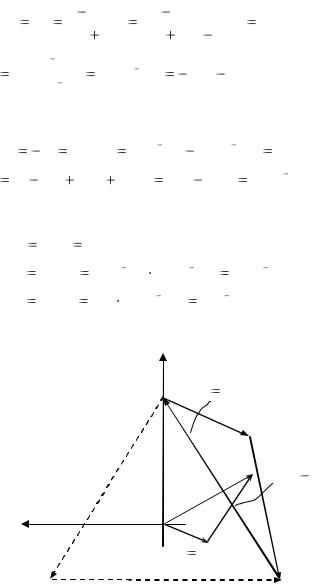

Скачиваний:

Добавлен:

01.05.2022

Размер:

865.28 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

220e

j30

Uab

Ibc

Ica

Zbc

Zca

100

j100

220e

j150

0,98e

j123

0,53

j0,82 A.

223,6e

j27

Линейные токи определим с помощью первого закона Кирхгофа

				2,2e	j60	0,98e	j123
IA	IB	Iab	- Ica	2,2e		0,98e
1,1	j1,9	0,53		j0,82	1,63	j1,08 1,96e j34 A.

Ток в линейном проводе фазы С отсутствует. Фазные напряжения приемников

220e

j30

U ab

U AB

141e

j45

0,98e

j123

138e

j168

Ubc

Zbc Ibc

100 0,98e

j123

98e

j123

Uca

Zca Ica

Топографическая диаграмма, совмещенная с векторной диаграммой токов построена на рис. 2.16.

АUAB Uab

Uca

	I A =	IB

Iab


	Ibc	Ica	Ubc
UCA	Ibc	Ica
UCA
С			В
		U BC

Рис. 2.16

КОНТРОЛЬНАЯ РАБОТА №3

АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

ПОСТОЯННОГО ТОКА

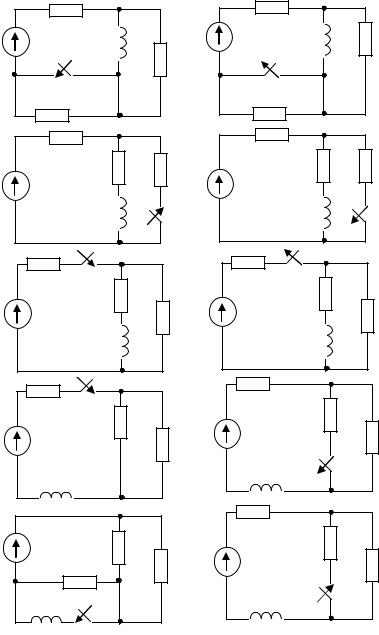
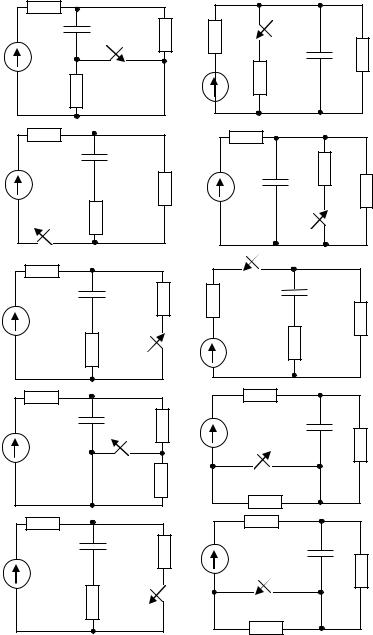
В линейных электрических цепях, схемы которых изображены на рис. 3.1 и 3.2 осуществляется коммутация, производимая идеальным ключом. Схемы содержит активные и реактивные элементы, параметры которых согласно варианту указаны в таблице.

1. Рассчитать классическим методом переходные функ-

ции:

а) ток и напряжение индуктивной катушки в схеме рис. 3.1; б) напряжение и ток конденсатора в схеме рис. 3.2.

2. В интервале времени от 0 до 5/|р| построить графики переходных функций тока и напряжения, рассчитанных в п.1.

Номер схемы на рис. 3.1 и 3.2 выбирается по последней цифре номера зачетной книжки студента; параметры элементов схемы выбираются по таблице по предпоследней цифре номера зачетной книжки.

№	E,	R1,	R2,	R3,	L,	C,
вар.	B	Ом	Ом	Ом	мГн	мкФ

0	20	40	30	10	10	15
1	10	20	60	15	100	20
2	50	25	25	20	10	25
3	10	5	10	5	20	10
4	50	100	50	150	100	30
5	40	20	40	30	100	50
6	40	20	40	30	200	10
7	100	200	100	200	150	50
8	50	20	30	100	250	20
9	200	150	250	200	300	100

Е	R1		Е	R1
				R1	R2
		L		L
		L		L
			R3
0)	R2		1)	R3
0)			1)

Е	R1	R2	Е
Е		R2	Е
			R3
		L
2)			3)
2)

Е	R1	R2	Е
Е		R2	Е
			R3
		L
4)			5)

R1	R2
	R2	R3
	L

R1	R2
	R2
	R3
	L

	R1	Е	R1	R2
Е	R1	Е		R2
Е		R2
		R3		R3
		R3
6)	L	7)		L
6)	L	7)

Е			Е	R1	R2
		R1	Е		R2
		R1
	R2	R3			R3
8	L		9)		L
8	L		9)

Рис. 3.1

Е	R1		R3	R1
Е		C	R3	R1		C	R3
		C		10		C
				10
				Е		R2
	R2					R2
	R2
0)				1)
Е	R1	C		Е	R1	R2
		C

			R3			C	R3
						C
2)		R2
2)				3)
Е	R1	C	R3	R1		C
Е		C	R3	R1		C
				10			R3
				Е
4)		R2				R2
		R2
				5)
				5)

Е	R1	C	R3
Е		C	R3	Е
				Е
6)			R2	7)
6)				7)
Е	R1	C	R3
Е		C	R3	Е
				Е
8)		R2
8)				9)
				Рис. 3.2
				42

C R3

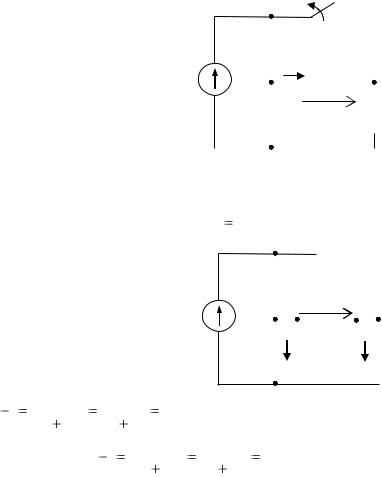
Пример расчета контрольной работы №3

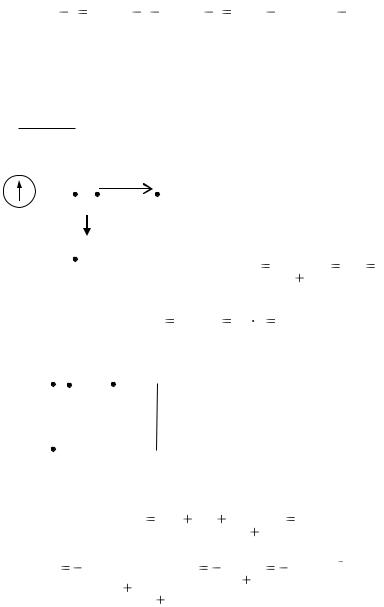
3.1. В цепи, схема которой приведена на рис. 3.3, происходит коммутация. Рассчитать переходные функции напряжения и тока конденсатора и построить их временные зависимости. Расчет выполнить классическим и операторным методами.

Исходные

данные

для

расчета:

Е=20

В,

R1=R2=R3=10 Ом, R4=30 Ом,

С=10 мкФ.

Решение.

Определим,

iС(t)

пользуясь

алгоритмом

рас-

чета переходных процессов,

uC(t)

функцию изменения во вре-

мени напряжения конденса-

тора		Рис. 3.3
	u C(t)=uCсв(t)+uCпр.

	Ток конденсатора рассчитаем по закону Ома, записанно-

му для мгновенных значений iC (t)

Определим независи-

мые начальные условия.

В установившемся до- Е коммутационном режиме в ветви с конденсатором ток отсутствует и в цепи (рис. 3.4) в параллельных ветвях протекают токи

i2	(0 )		E	20	1 A,

		R1	R2	10 10

duC

(t)

uC(0-)

i4(0-)

i2(0-)

Рис. 3.4

i4	(0 )		E	20	0,5 A.

		R3	R4	10 30

Напряжение конденсатора в докоммутационной цепи

найдем по второму закону Кирхгофа

uC (0 ) R2i2 (0 ) R4i4 (0 ) 10 1 30 0,5 5 B.

Согласно второму закону коммутации напряжение конденсатора не может измениться мгновенно, поэтому начальное значение этого напряжения будет равно его докоммутацион-

ному значению:

uC(0+)=uC(0-)= -5 В.

Принужденное значение напряжения конденсатора опре-

делим, рассчитав токи и

напряжения в

установив-

шемся режиме в цепи после

uCПР

коммутации (рис. 3.5). Ток

в четвертом резисторе от-

сутствует и в цепи протека-

i2ПР

ет только ток

i2ПР

1 A.

Рис. 3.5

Тогда напряжение конденсатора

uСПР

R2i2ПР

10 1

10 В.

Составим характеристическое

уравнение. Для

этого

1/Ср

найдем

входное

сопротивление

пассивной

части

схемы

после

коммутации

относительно

ра-

зомкнутых зажимов ab (рис. 3.6).

В рассматриваемой цепи источ-

ник

напряжения заменяется

ко-

Рис. 3.6

роткозамкнутым

участком,

конденсатор операторным сопротивлением 1/Сp:

Zab

(p)

R1R2

0 .

Откуда

105

2857

c 1.

C(R

R1R 2

)

R 2

Так как характеристическое уравнение имеет один корень р= -2857 1/с, свободная составляющая напряжения име-

ет вид:	u	CCB	(t) Be 2857 t .
		CCB
Определим постоянную интегрирования В. Для этого,
рассмотрим искомую функцию напряжения
			u C(t)=uCсв(t)+uCпр= Be 2857 t 10
в момент времени t=0+:				u C(0+)= B 10 .

Начальное значение напряжения конденсатора uC(0+)=-5 В.

Получим уравнение			B 10 = -5, и найдем постоянную интег-
рирования	В= -15 В.
Искомая переходная функция напряжения
		u C(t)=			15e 2857 t 10 , В.
Определим переходную функцию тока в ветви с конден-
сатором с помощью закона Ома:
iC (t)	C	duC (t)		d(	15e 2857 t	10)
		dt			dt

10 10 6 ( 15)(			2857)e 2857 t			0,428e 2857 t , A.

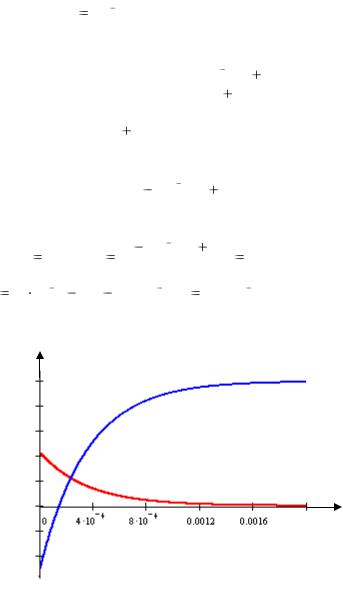
Графики временных зависимостей переходных функций напряжения и тока конденсатора представлены на рис. 3.7.

iC, uC

uC(t)

iC (t)

t, c

Рис. 3.7

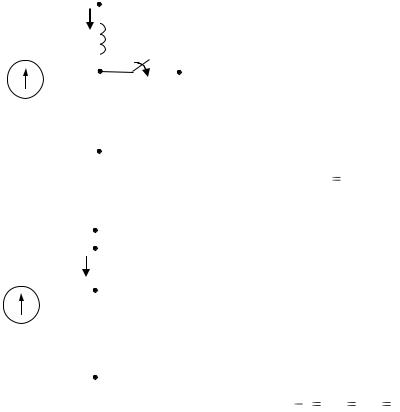
3.2. В цепи, схема которой приведена на рис. 3.8, происходит коммутация. Рассчитать переходные функции напряжения и тока индуктивной катушки и построить их временные

зависимости. Расчет выполнить классическим методом.

Исходные данные для расчета: Е= 30 В,

R1=R2=R3=10 Ом, L=1 мГн.

Решение.

Определение переходных функций начнем с

нахождения тока индуктив-

iL(t)

ной катушки,

как

суммы

свободной и принужденной

составляющих

iL(t) = iLсв(t) + iLпр.

Напряжение на зажи-

мах катушки найдем с по-

мощью

закона

Ома

для

мгновенных значений

Рис.

3.8

uL (t)

diL

(t)

Определим независимые начальные условия.

Учитывая, что в цепи

постоянного тока в устано-

iL(0-)

вившемся режиме идеальная

индуктивная катушка пред-

ставляет собой участок с со-

противлением равным нулю,

легко рассчитать ток катуш-

ки в схеме до коммутации

(рис. 3.9)

Рис.

3.9

iL (0

)

Согласно первому закону коммутации ток индуктивной катушки в момент коммутации не может измениться мгновенно и в первый момент остается равным докоммутационному значению

iL(0+)=iL(0-)=3 А.

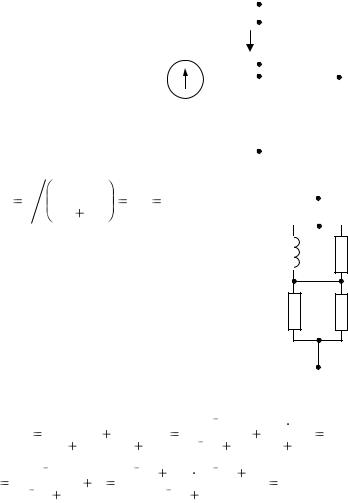
Найдем принужденное значение тока катушки. Для этого

рассчитаем величину тока в

установившемся

режиме

цепи после коммутации

iLПР

(рис. 3.10).

Так как индук-

тивная катушка представля-

ет собой короткозамкнутый

участок цепи, то ток в рези-

сторе R3 отсутствует, а ток

катушки определим, как:

Рис. 3.10

iLПP

R1R2

6 A.

Составим характеристическое уравнение путем определения входного сопротивления Z(p) пассивной части цепи после коммутации (рис. 3.11). В рассматриваемой цепи источник напряжения заменяется короткозамкнутым участком, а индуктивная катушка операторным сопротивлением Lp. Находим входное сопротивление относительно разомкнутых входных зажимов цепи:

Lp	R3
R1	R2

Рис. 3.11

			LpR	3			R R			2		10	2 p		10 10
Z(p)				3				1		2
Z(p)		Lp R			3	R		!	R		2	10 3 p	10		10 10
		Lp R				R			R			10 3 p	10		10 10

	10		2 p		5	10 2 p						0,5 10	2 p	50	0.

10 3 p			10						(10 3 p 10)20
10 3 p			10						(10 3 p 10)20

Характеристическое уравнение имеет вид

1,5·10-2р+50=0.

Так как уравнение имеет один корень р = -3333 1/с, то свободную составляющую тока катушки запишем, как

		iLCB (t) Аеpt Ae 3333 t .
Для нахождения постоянной интегрирования А рас-
смотрим искомую функцию тока
	iL(t)=iLсв(t)+iLпр= Ae 3333 t 6
в момент времени t=0+:		iL(0+)=А+6.
Так как согласно закону коммутации iL(0+)=3 А, то полу-
чим уравнение	А+6=3,

откуда найдем значение постоянной интегрирования А= -3 (А).

Переходная функция тока катушки

iL(t)=-3е-3333t+6 (А).

Напряжение индуктивной катушки

u		(t)	L	diL (t)	10	3 d(	3e 3333 t 6)
	L			dt			dt


		10 3 (	3333)(		3)e 3333 t		10e 3333 t (B).

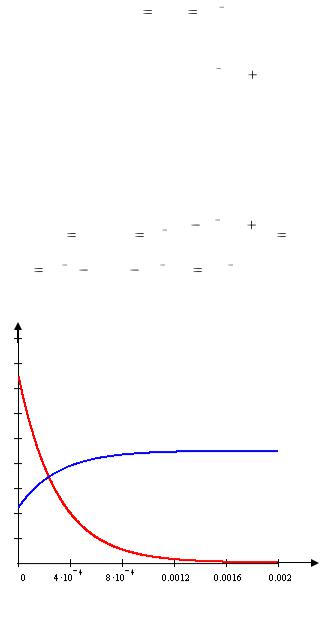
Графики временных зависимостей переходных функций напряжения и тока катушкиа представлены на рис. 3.12.

uL(t), iL(t)

iL(t)

uL(t)

t, c

Рис. 3.12

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

Е	R1		R3	R1
Е		C	R3	R1		C	R3
		C		10		C
				10
				Е		R2
	R2					R2
	R2
0)				1)
Е	R1	C		Е	R1	R2
		C

			R3			C	R3
						C
2)		R2
2)				3)
Е	R1	C	R3	R1		C
Е		C	R3	R1		C
				10			R3
				Е
4)		R2				R2
		R2
				5)
				5)

Е	R1		R3	R1
Е		C	R3	R1		C	R3
		C		10		C
				10
				Е		R2
	R2					R2
	R2
0)				1)
Е	R1	C		Е	R1	R2
		C

			R3			C	R3
						C
2)		R2
2)				3)
Е	R1	C	R3	R1		C
Е		C	R3	R1		C
				10			R3
				Е
4)		R2				R2
		R2
				5)
				5)

Е	R1		R3	R1
Е		C	R3	R1		C	R3
		C		10		C
				10
				Е		R2
	R2					R2
	R2
0)				1)
Е	R1	C		Е	R1	R2
		C

			R3			C	R3
						C
2)		R2
2)				3)
Е	R1	C	R3	R1		C
Е		C	R3	R1		C
				10			R3
				Е
4)		R2				R2
		R2
				5)
				5)