Учебники 80118

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ВЕРОЯТНОСТНЫХ ЗАДАЧ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы по курсу

«Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения

Часть 3

A B

Воронеж 2013

Составитель канд. физ.-мат. наук В.В. Дежин

УДК 517 Использование математического моделирования при ре-

шении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 3 / ФГБОУВПО «Воронежский государственный технический университет»; сост. В.В. Дежин. Воронеж, 2013. 40 с.

Методические указания предназначены в качестве руководства для самостоятельного изучения студентами направления 080100 «Экономика» профиля «Экономика предприятий и организаций» (Э) очной формы обучения курса «Теория вероятностей и математическая статистика». Методические указания включают в себя 3 занятия и содержат основные понятия, ссылки на литературу, пояснения и примеры, контрольные вопросы и задачи, форму отчетности.

Предназначены для студентов третьего семестра второго курса.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле Э-ТВиМС-3.pdf.

Табл. 7. Ил. 18. Библиогр.: 22 назв.

Рецензент канд. физ.-мат. наук, доцент А.Н. Шелковой Ответственный за выпуск зав. кафедрой д-р физ.-мат. на-

ук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУВПО «Воронежский государственный технический университет», 2013

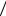
Занятие № 7 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

7.1.Основные понятия

Вбольшинстве задач теории вероятностей более удобным является описание результатов вероятностных экспериментов не в понятии событий и их вероятностей, а с помощью числовых функций, определенных на событиях, и вероятностей принимать этими функциями те или иные значения. Это связано с тем, что к числовым функциям можно непосредственно применять хорошо развитый аппарат математического анализа. Такой подход дает возможность решать значительно более широкий круг задач, связанных с исследованием случайный явлений.

Рассмотрим ряд примеров вероятностных экспериментов,

вкоторых естественным образом появляется понятие случай-

ной величины (СВ).

1. Вероятностный эксперимент – бросание двух монет на гладкую горизонтальную поверхность. Фиксируется число выпавших гербов, возможные значения: 0, 1, 2 – это СВ.

2. Вероятностный эксперимент – испытание некоторого технического устройства. Фиксируется:

а) число отказов устройства за определенный промежуток времени, возможные значения СВ: 0, 1, …;

б) время безотказной работы устройства, возможные значения – любое неотрицательное число (длина временного промежутка).

Вкаждом из приведенных экспериментов мы имеем дело с некоторой величиной, принимающей случайным образом различные числовые значения. Такие величины и называются случайными. При первом знакомстве с понятием случайной величины можно дать следующее нестрогое определение.

Случайной величиной называется переменная величина, принимающая в результате опыта, в зависимости от его случайного исхода, то или иное числовое значение.

Таким образом, для задания случайной величины прежде всего необходимо знать те значения, которые она может принимать. Однако этого недостаточно. Действительно, во втором, приведенном выше примере, для любого устройства возможные значения числа отказов за определенный промежуток времени одни и те же. Но надежное устройство отличается от ненадежного тем, что большое число отказов в его работе встречается реже. Поэтому для задания СВ необходимо знать не только множество ее возможных значений, но и как часто, т.е. с какой вероятностью она принимает эти значений. В теории вероятностей говорят, надо задать закон распределения СВ.

Прежде чем дать строгое определение понятия СВ, рассмотрим подробнее, как оно появляется в вероятностном эксперименте с бросанием двух правильных монет.

Пространство элементарных событий в этом эксперименте имеет вид: 1, 2, 3, 4 ГГ, ГЦ, ЦГ, ЦЦ , где Г

– обозначает выпадение герба, а Ц – цифры. События i рав-

новозможные, поэтому вероятности всех элементарных исхо-

будет зависеть от элементарных исходов, т.е. будет функцией элементарных событий i , принимающей следующие значе-

ния: X 1 2, X 2 1, X 3 1, X 4 0. В силу слу-

чайности исходов опыта значения функции X X также являются случайными, т.е. X есть случайная величина.

Зная вероятности P i элементарных исходов, можно найти вероятности того, что СВ X примет то или иное значение. Для примера найдем вероятность P X 1 случайной ве-

личине придать значение единице. Эта вероятность будет равна вероятности события X 1 , которое наступает, если реализуется один из элементарных исходов 2 ГЦ или3 ЦГ , т.е. есть X 1 ГЦ, ЦГ . Отсюда P X 1

ных событий , для которой множество элементарных событий вида : x1 X x2 является наблюдаемым событием для любых действительных чисел x1 и x2 , т.е.

: x1 X x2 A . Короче, случайная величина – это отображение X : множества элементарных собы-

тий в множество действительных чисел такое, что: x1 X x2 A для всех x1, x2 .

Условимся в дальнейшем обозначать случайные величины большими латинскими буквами X, Y, Z, , а их возможные значения соответствующими маленькими буквами: x, y, z .

Поясним смысл приведенного определения, особенно его второй части. Как видно из рассмотренных примеров, множеством значений случайной величины могут быть различные подмножества числовой прямой: дискретные множества точек, промежутки, а также их объединения и пересечения. Все такие подмножества могут быть получены с помощью операций объ-

единения, пересечения и дополнения из множества всевозможных интервалов вида x1, x2 при различных x1 и x2 . Отсюда и соответствующие события могут быть получены из событий: x1 X x2 с помощью соответствующих операций

над событиями. Таким образом, для того, чтобы иметь возможность находить вероятность попасть случайной величине в какое-то множество на числовой прямой, достаточно потребовать, чтобы можно было находить вероятности событий вида: x1 X x2 . Это означает, что такие события должны

быть наблюдаемыми, т.е. они должны принадлежать - алгебре событий. Это требование и зафиксировано в определении случайной величины.

Следует отметить, что в теоретико-вероятностных задачах явная зависимость СВ X от чаще всего не имеет значения. Для решения большинства задач не требуется построения вероятностного пространства , A, P . Вместо этого можно

рассматривать новое вероятностное пространство , A, P , в

котором пространством элементарных событий является числовая прямая (т.е. множество всевозможных значений случайной величины), в качестве -алгебры A принимается - алгебра борелевских множеств, т.е. совокупность подмножеств B , полученных из интервалов с помощью счетного числа операций объединения, пересечения и взятия дополнения, а вероятность P определяется заданием вероятности P X B

для любых борелевских подмножеств B числовой прямой.

Задание вероятности P X B для любых борелев-

ских подмножеств B числовой оси называется законом распределения вероятностей случайной величины X .

В множестве всех случайных величин можно выделить два основных класса дискретных и непрерывных величин.

Можно дать следующие определения (не являющиеся строгими).

Случайная величина является дискретной (ДСВ), если множество ее значений конечно или счетно.

Случайная величина называется непрерывной (НСВ), если множество ее возможных значений несчетно и непрерывно заполняет некоторый интервал (конечный или бесконечный) на числовой оси.

СВ встречаются повсюду в окружающей нас действительности: время безотказной работы компьютера, число отказавших элементов некоторого устройства, курс доллара, цена товара, время ожидания транспорта, прибыль или убытки фирмы. Продумайте, какие из приведенных СВ являются дискретными, а какими непрерывными. Следует уяснить, что на практике объектом изучения является не абстрактная непрерывная СВ, а, как правило, результат измерений некоторого параметра прибором с определенной ценой деления шкалы.

Говорят, что задан закон распределения дискретной случайной величины, если известны ее возможные значения

n 1

Простейшей формой задания закона распределения дискретной случайной величины (ДСВ) является таблица, в верхней строке которой перечислены всевозможные значения случайной величины в возрастающем порядке, а в нижней – соответствующие им вероятности.

Таблица 1

Такую таблицу называют рядом распределения дискретной случайной величины (ДСВ) X .

Графическое представление ряда распределения называ-

ют многоугольником распределения ДСВ (рис. 1).

p

i

7.2. Примеры решения задач

Пример 1. Устройство состоит из четырех независимо работающих элементов. Вероятность отказа каждого элемента в одном испытании равна 0,2. Составить закон распределения числа отказавших элементов в одном испытании.

Решение. Дискретная случайная величина (ДСВ) X (число отказавших элементов в одном испытании) имеет следующие возможные значения: x1 0 (ни один из элементов устройства не отказал), x2 1 (отказал один элемент), x3 2 (отказали два элемента), x4 3 (отказали три элемента), x5 4

(отказали четыре элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию, n 4, p 0,2, q 1 p 0,8, получим:

P4 0 q4 0,84 0,4096;

P4 1 C41 pq3 4 0,2 0,83 0,4096;

P4 2 C42 p2q2 6 0,22 0,82 0,1536; P4 3 C43p3q 4 0,23 0,8 0,0256; P4 4 p4 0,24 0,0016.

Контроль: 0,4096+0,4096+0,1536+0,0256+0,0016=1. За-

пишем искомый биномиальный закон распределении ДСВ X (пишут X B(n, p)):

p

i

p

3

Пример 2. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения ДСВ X – числа стандартных деталей среди отобранных.

Решение. ДСВ X распределена по гипергеометрическому закону, вероятности ее возможных значений находятся по

формуле P X m CMm CNn mM 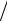CNn , где N – число деталей в партии, M – число стандартных деталей в партии, n – число отобранных деталей, m – число стандартных деталей среди отобранных. ДСВ X имеет следующие возможные значения: x1 1 (среди отобранных деталей содержится одна стандарт-

7.3.Контрольные вопросы и задания

1.Приведите примеры случайных величин в информационных системах.

2.Назовите два типа случайных величин.

3.Что такое закон распределения ДСВ?

4.Как строится многоугольник распределения ДСВ?

5.Чем отличается непрерывная СВ от дискретной СВ?

6.Чему равна вероятность P X x0 для НСВ?

7.Разберитесь в решении задач [2], №№ 164, 166, 170, 172, 174, 182.

7.4.Задачи для самостоятельной работы

1. Решите задачи [2], №№ 165, 167-169, 173, 175..

Форма отчетности: устный опрос, контрольная работа, типовой расчет, коллоквиум, экзамен.

Занятие № 8

ФУНКЦИЯ И ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН

8.1.Основные понятия

Вобщем случае наиболее распространенной формой записи закона распределении как для дискретных, так и для непрерывных случайных величин (СВ) является функция распре-

деления.

Функцией распределения случайной величины X называется функция FX x действительной переменной x ,

определяемая формулой

то есть FX x это вероятность того, что случайная вели-

чина X примет значение меньшее некоторого числа x.

Функция распределения FX x или просто F x являет-

ся самой полной характеристикой СВ; задать СВ означает задать ее функцию распределения.

Рассмотрим основные свойства функции распределения. 1. F x – неубывающая функция на всей числовой оси,

то есть если x1 x2 , то F x1 F x2 . 2. F x непрерывна слева, то есть

lim F x F x0 0 F x0 .

x x0 0

3. Для всех x выполняется соотношение 0 F x 1,

причем F 0, F 1.

Следствие. Вероятность того, что СВ заключена в определенных пределах, равна

Из формулы (8.5) в частном случае x1 x2 x получается выражение для вероятности принять СВ X значение x:

Для дискретной случайной величины (ДСВ) функция распределения является другой формой записи ее закона распределения. Зная ряд распределения ДСВ, можно записать ее функцию распределения и наоборот. Так, если известен закон

распределения СВ X , то ее функция распределения определяется следующим соотношением

Из формулы (8.3) видно, что функция распределения любой ДСВ является разрывной функцией. Она принимает постоянное значение в промежутках между соседними значениями xk 1, xk и возрастает скачком в точке разрыва x xk . Величи-

на скачка в точке xk согласно формуле (8.6) равна вероятности принять СВ значение xk :

F xk 0 F xk P X xk pk .

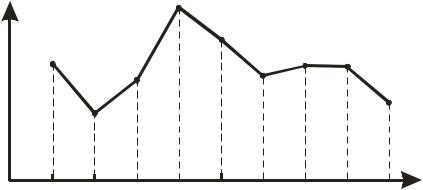
Типичный график функции распределения ДСВ изображен на рис. 4 для случая пяти возможных значений СВ.

В занятии 7 было дано нестрогое определение непрерывной случайной величины (НСВ) Приведем строгое определение НСВ.

Случайной величиной X называется непрерывной (аб-

солютно непрерывной), если существует неотрицательная

вероятностей (или просто плотностью распределения) случайной величины X .

Для НСВ плотность распределения вероятностей является основной характеристикой.

Плотность распределения вероятностей обладает сле-

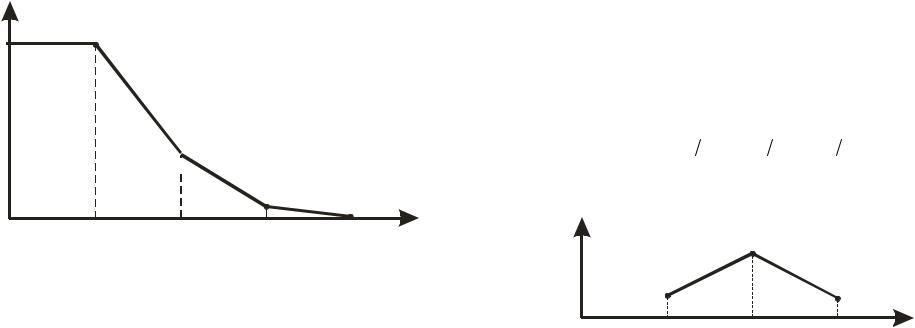
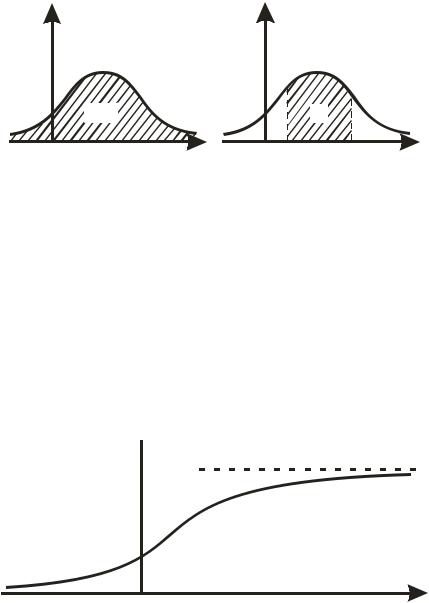
Приведенные свойства плотности распределения вероятностей имеют наглядную геометрическую интерпретацию, которая проиллюстрирована на рис. 5.

Рис. 5

Из определения (8.8) следует, что функция распределения НСВ является непрерывной функцией, поэтому согласно формуле (8.6) P X x F x 0 F x 0 , то есть вероятность

попасть в точку для НСВ равна нулю. Отсюда следуют следующие равенства:

P x1 X x2 P x1 X x2P x1 X x2 P x1 X x2 .

Типичный график функции распределения НСВ X изображен на рис. 6.

FX(x) 1

Рис. 6

8.2. Примеры решения задач

Пример 1. В условиях примера 1 из занятия 7 найти функцию распределения и начертить ее график.

Решение. Из найденного закона распределения

определяем, что при x 0 функция распределения

F x P X 0 0.

Если 0 x 1, то F x P X 1 P X 0 0,4096.

Если 1 x 2, то

F x P X 2 P X 0 P X 1

0,4096 0,4096 0,8192.

Если 2 x 3, то

F x P X 3 P X 0 P X 1 P X 2

0,4096 0,4096 0,1536 0,9728.

Если 3 x 4, то

F x P X 4 P X 0 P X 1 P X 2 P X 3

0,4096 0,4096 0,1536 0,0256 0,9984.

Соответствующий график функции распределения вероятностей изображен на рис. 7.

F(x)

0,9984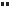1 0,9728

0,8192

0,4096

0

Рис. 7

Пример 2. В условиях примера 2 из занятия 7 найти функцию распределения и начертить ее график.

Решение. Из найденного закона распределения

Таблица 5

определяем, что при x 1 функция распределения

F x P X 1 0.

Если 1 x 2, то F x P X 2 P X 1 0,2.

Если 2 x 3, то

F x P X 3 P X 1 P X 2 0,2 0,6 0,8.

Если x 3, то

F x P X 3 P X 1 P X 2 P X 3

0,2 0,6 0,2 1.

Таким образом, искомая функция распределения имеет вид:0 при x 1

0,2 при 1 x 2

F x

0,8 при 2 x 3

1 при x 3

Соответствующий график изображен на рис. 8.

F(x)

1

0,8

0,2 0

Рис. 8

Пример 3. Функция распределения НСВ X (времени безотказной работы электронного устройства) равна

Найти: а) плотность распределения вероятностей; б) вероятность безотказной работы устройства за время x T .

Вероятность безотказной работы устройства за время x T определим по формуле (8.9):

P T X F F T 1 1 e 1 1e 0,37 .

Пример 4. Случайная величина эксцентриситета детали X имеет плотность распределения вероятностей

8.3.Контрольные вопросы и задания

1.Дайте определение функции распределения вероятностей случайной величины.

2.Назовите основные свойства функции распределения.

3.Чему равна вероятность того, что СВ заключена в определенных пределах.

4.Как определяется функция распределения для ДСВ?