
Учебники 80118
.pdf5.Изобразите типичный график функции распределения для ДСВ.
6.Приведите строгое определение НСВ.
7.Что такое плотность распределения вероятностей?
8.Приведите свойства плотности распределения вероят-
ностей.
9.Изобразите типичный график функции распределения для НСВ.
10.Чему равна вероятность попасть в точку для НСВ?
11.Разберитесь в решении задач [2], №№ 252, 256, 258, 260, 262, 264, 267, 271.
8.4.Задачи для самостоятельной работы
1.Решите задачи [2], №№ 253, 254, 257, 259, 261, 263, 265, 266, 269, 270, 273.
Форма отчетности: устный опрос, контрольная работа, типовой расчет, коллоквиум, экзамен.
Занятие № 9
ПРИМЕРЫ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
Здесь будут приведены примеры распределений, наиболее часто встречающихся в практических приложениях теории вероятностей
9.1.Законы распределения ДСВ
9.1.1.Геометрическое распределение
Будем рассматривать последовательность независимых испытаний в схеме Бернулли с вероятностью успеха p и фик-
сировать число k испытаний, проведенных до появления первого успеха включительно. Успех может наступить сразу в первом испытании и тогда k 1; может не наступить в первом, но осуществиться во втором испытании, тогда k 2, и так далее. Таким образом, число испытаний, проведенных до появления первого успеха, является случайной величиной дискретного типа с целочисленными возможными значениями 1, 2, … По теореме умножения для независимых событий находим вероятность принять рассматриваемой случайной величине значение k :
p P X k qk 1p , |
(q 1 p). |
(9.1) |
|
k |
|
|
|
|
|
|
|
Нетрудно проверить, что pk |
1. Итак, формула (9.1) задает |
||
k 1 |
|
|
|
распределение вероятностей, которое из-за связи его с геометрической прогрессией называется геометрическим.
Пример 1. Производятся последовательные независимые испытания пяти электронных устройств. Вероятность того, что устройство пройдет испытание успешно, равна 0,6. Каждое следующее устройство испытывается только в том случае, когда предыдущее прошло испытание успешно. Найти закон распределения ДСВ X – числа испытанных в данном эксперименте испытания устройств.
Решение. Замечаем, что данная ДСВ X распределена по
геометрическому закону с параметрами |
p 0,4 и |
q 0,6. По |
||||||
формуле (9.1) находим вероятности p1, |
p2 , p3, |
p4 . Вероят- |
||||||
ность |
p 0,64 0,4 0,64 0,6 0,64 . |
Получаем |
соответст- |
|||||
|
|
5 |
|
|
|
|
|
|
вующий ряд распределения: |
|
|
Таблица 6 |
|||||
|
|
|
|
|
|
|
||
|
xk |
|
1 |
2 |
3 |
4 |
5 |
|
|
pk |
|
0,4 |
0,24 |
0,144 |
0,0864 |
0,1296 |
|
19 |
20 |

Соответствующий многоугольник распределения выглядит следующим образом (рис. 9):
p
k
p
0,4




 1
1
0,24 |
|
|
p2 |
|
|
|
|
|
|
p3 |
p4 |
p5 |
|
|
|
|
|
|
||
0 |
1 |
2 |
3 |
4 |
5 |
xk |
|
|
|
Рис. 9 |
|
|
|
|
9.1.2. Биномиальное распределение B n, |
p |
|
|||
Число успехов в серии из n независимых испытаний с неизменной вероятностью p успеха является случайной величиной X , принимающей значения 0, 1, 2, …, n. Вероятность случайной величине X принять значение m определяется формулой Бернулли
P X m P |
m Cm pmqn m |
, |
m 0,1, 2, , n. (9.2) |
n |
n |
|
|
n
Заметим, что Cnm pmqn m p q n 1 есть разложение по
m 0
формуле бинома Ньютона выражения p q n и, следователь-
но, формула (9.2) задает биномиальное распределение. Биноми-
альное распределение является одним из важнейших распреде-
лений дискретных случайных величин. Оно само является предельным для некоторых распределений, и из него, как следует из предельных теорем в схеме Бернулли, при определенных условиях вытекают другие распределения.
В примере 1 из занятия 7 найден биномиальный закон распределения ДСВ X ( X B n, p ) и построен соответст-
вующий многоугольник распределения (рис. 2).
9.1.3. Распределение Пуассона
Случайная величина X , принимающая целочисленные значения 0, 1, 2, …, имеет пуассоновское распределение с па-
раметром , если
P X m |
m |
e , |
m 0,1, 2 |
(9.3) |
|
m!
Взанятии 6 была рассмотрена предельная теорема Пуассона, из которой следует, что распределение Пуассона может
быть получено из биномиального предельным переходом n , p 0 при условии np (0,1÷10,0) и в этом случае интерпретируется как закон редких явлений.
Распределение Пуассона является хорошей математической моделью случайного числа появлений определенных событий в фиксированном промежутке времени и находит широкое применение в теории случайных процессов.
Пример 2. Электронная аппаратура состоит из 1000 элементов, каждый из которых независимо от остальных выходит
из строя за время T с вероятностью p 5 10 4. Найти закон распределения ДСВ X – числа элементов, вышедших из строя за время T . Найти вероятность того, что за время T откажет хотя бы один элемент.
Решение. Значение параметра np 1000 5 10 4 0,5 принадлежит указанному выше интервалу, поэтому по формуле (9.3) получим соответствующий ряд распределения:
21 |
22 |
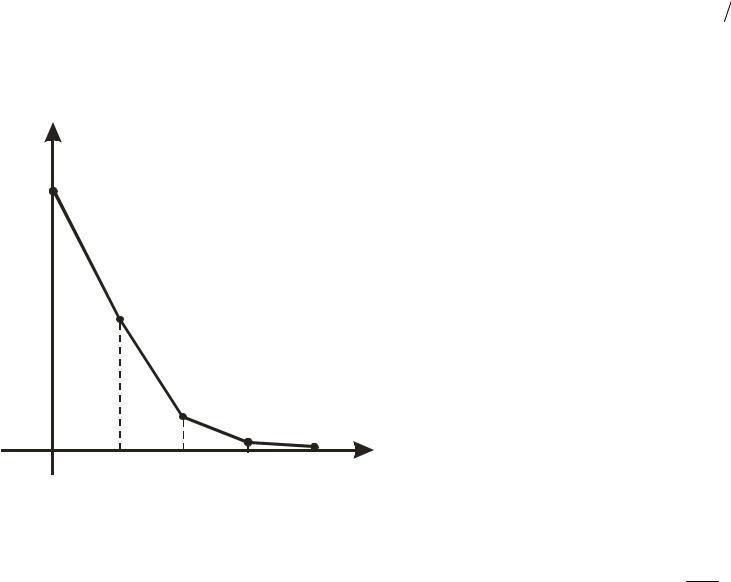
Таблица 7
xk |
0 |
1 |
2 |
3 |
4 |
… |
pk |
0,6065 |
0,3033 |
0,0758 |
0,0126 |
0,0016 |
… |
Соответствующий многоугольник распределения выглядит следующим образом (рис. 10).
p
k
p
0,6065 1
p
 2
2
p
 3
3
p4 p5
0 |
1 |
2 |
3 |
4 |
xk |
|
|
Рис. 10 |
|
|
|
9.1.4. Гипергеометрическое распределение
Рассмотрим следующую задачу. В урне находится N шаров, из которых M белых. Пусть один за другим без возврата (или одновременно, что одно и то же) вынимается n шаров (n M ). Тогда вероятность того, что среди этих вынутых n шаров будет m белых, равна
P |
n, m |
Cm |
Cn m |
Cn |
(m 0,1, , n). |
(9.4) |
N,M |
|
M |
N M |
N |
|
|
Случайная величина X |
называется распределенной ги- |
|||||
пергеометрически, |
если |
возможные |
значения m 0,1, , n |
|||
она принимает с вероятностями P X m PN,M n, m , опре-
деляемыми формулой (9.4). Числа N, M, n – параметры рас-
пределения.
Гипергеометрическое распределение, таким образом, описывает осуществление признака в выборке без возвращения. Если N очень велико по сравнению с n, то не имеет существенного значения, возвращаются шары обратно или нет, и формула (9.4) может быть приближенного заменена формулой (9.2) биномиального распределения.
В примере 2 из занятия 7 найден гипергеометрический закон распределения ДСВ X и построен соответствующий многоугольник распределения (рис. 3).
9.2.Законы распределения НСВ
9.2.1.Равномерное распределение R a, b
Непрерывная случайная величина X называется распре-
деленной равномерно на отрезке a, b , если ее плотность рас-
пределения вероятностей постоянная на данном отрезке:
1 |
, если |
x a, b |
|
|
|
||
|
|||
pX x b a |
|
(9.5) |
|
|
если |
x a, b . |
|
0, |
|||
Функция распределения для равномерного закона:0 при x a
x a
FX x при a x b (9.6)
b a
1 при x b.
23 |
24 |

Графики плотности распределения и функции распределения для равномерного закона приведены на рис. 11.
p (x) |
|
|
FX(x) |
|
|
X |
|
|
|
|
|
1 |
|
|
1 |
|
|
b-a |
|
|
|
|
|
|
|
|
|
|
|
0 a |
b |
x |
0 a |
b |
x |
|
|
Рис. 11 |
|
|
|
Вероятность равномерно распределенной СВ принять значение из интервала , , целиком лежащего в отрезке
a, b , равна
|
dx |
|
|
|
|
P X |
|
|
|
. |
(9.7) |
b a |
b a |
||||
|
|
|
|
|
|
Заметим, что такое же значение получается для вероятности попасть в промежуток , a, b точке, случайно брошен-
ной на отрезок a, b в схеме геометрических вероятностей.
Это как раз и есть отражение того, что все исходы в схеме геометрических вероятностей равновероятны.
На практике равномерное распределение реализуется при измерении тех или иных физических величин приборами, имеющими шкалу. Ошибка округления отсчета до ближайшего деления является случайной величиной, значения которой с одинаковой вероятностью лежат между соседними делениями шкалы измерительного прибора. Кроме того, равномерное распределение широко используется в статистическом моделировании (метод Монте-Карло).
Пример 3. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего деления шкалы. Найти вероятность того, что будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
Решение. Ошибку округления отсчета можно рассматривать как СВ X , которая распределена равномерно в интервале между соседними делениями шкалы (например, между 0 и 0,2),
т.е. X R 0; 0,2 . Так как 1 b a 1
b a 1 0,2 5, то
0,2 5, то
5, |
если |
x 0; |
0,2 |
pX x |
если |
x 0; |
0,2 . |
0, |
|||
|
|
|
|
а) Ошибке отсчета меньшей 0,04 будут соответствовать два симметричных интервала: (0; 0,04) и (0,16; 0,2) (рис. 12).
0 0,04 |
0,16 0,2 |
x |
|
Рис. 12 |
|
По формуле (9.7) получим
P 0 X 0,04 P 0,16 X 0,2 2P 0 X 0,04
0,04
2 5dx 2 5 0,04 0,4.
0
б) Ошибке отсчета большей 0,05 соответствует интервал
(0,05; 0,15) (рис. 13).
0 |
0,05 |
|
0,15 |
0,2 |
x |
|
|
|
Рис. 13 |
|
|
||
По формуле (9.7) получим |
0,15 |
|
|
|
||
P 0,05 X 0,15 |
5dx 5 0,15 0,05 0,5. |
|||||
|
||||||
|
|
0,05 |
|
|
|
|
25 |
26 |

9.2.2. Показательное (экспоненциальное) распределение Ex
Непрерывная случайная величина X , принимающая неотрицательные значения, имеет показательное (экспоненци-
альное) распределение с параметром 0 ( X Ex ), если
ее плотность распределения вероятностей задается формулой
|
|
0, |
|
если |
x 0 |
p |
|
|
|
|
(9.8) |
X |
x |
, |
если |
||
|
e x |
x 0. |
|||
|
|
|
|
|
|
Показательное распределение является непрерывным аналогом геометрического распределения.
Функция распределения вероятностей для показательного закона имеет вид:
0, если x 0
FX x x (9.9)
1 e , если x 0.
Графики плотности распределения и функции распределения для показательного закона приведены на рис. 14.
p (x) |
FX(x) |
X |
|
|
1 |
0 |
x |
0 |
x |
Рис. 14
Показательное распределение часто встречается в различных приложениях теории вероятностей: в теории массового обслуживания, когда СВ X – время ожидания при техническом обслуживании или X – длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции, в
теории надежности, где, например, СВ X – срок службы радиоэлектронной аппаратуры.
В примере 3 из занятия 8 найдена вероятность безотказной работы электронного устройства за время x T в случае СВ X Ex .
9.2.3. Нормальное распределение N m,
Нормальный закон распределения (закон Гаусса) занимает особое место в теории вероятностей. Он наиболее часто встречается на практике. Связано это с тем, что нормальное распределение является предельным для многих других распределений. С одним из таких случаев мы уже встречались при рассмотрении предельных теорем Муавра-Лапласа.
Непрерывная случайная величина X называется распре-
деленной по нормальному закону (закону Гаусса) с параметра-
ми m и 0 ( X N m, |
), если плотность распределе- |
|||||||
ния вероятностей для нее имеет вид |
|
|
||||||
pX x |
|
1 |
|
e |
x m 2 |
|
|
|
|
|
2 2 , |
x . |
(9.10) |
||||
|
|
|
|
|||||
|
||||||||
|
|
2 |
|
m и |
|
|||
Вероятностный смысл параметров |
будет пояснен в |
|||||||
следующем занятии.
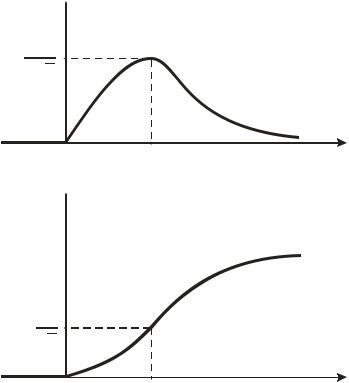
График плотности распределения нормального закона называется кривой Гаусса. Она имеет максимум в точке x m; симметрична относительно прямой x m; при x кривая Гаусса асимптотически приближается к оси Ox . При изменении параметра m кривая Гаусса, не меняя формы, смещается вдоль оси абсцисс. Параметр – расстояние от прямой x m до точек перегиба. Поведение кривой при изменении параметра показано на рис. 15. Отметим, что в любом случае площадь под кривой Гаусса в силу условия нормировки остается равной единице.
27 |
28 |

p (x)
X
3
3 2 1
2
1
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15 |
|
|
|
|
|
|
|
|
|
|
|||||||
Функция распределения для нормального закона: |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
t m 2 |
|
|
|
|
|
|
|
x m |
|
t2 |
|
|
|
|
||||||
|
x |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||
F |
|
|
|
|
e 2 2 |
dt |
|
|
|
|
e 2 dt |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
X |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m |
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x m |
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
x m |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 2 dt |
|
|
0 |
|
|
|
. (9.11) |
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График функции распределения (9.11) приведен на рис. 16.
 FX(x) 1
FX(x) 1





0,5







0 |
m |
x |
Рис. 16
29
Функция x – интеграл ошибок и 0 x – функция
Лапласа затабулированы (для положительных значениях аргумента имеются подробные таблицы). При отрицательных значениях аргумента используются свойства: x 1 x ,
0 x 0 x .
На практике часто требуется найти вероятность того, что СВ X N m, примет значение из заданного интервала
, . Эта вероятность находится по следующей формуле:
P X FX FX
m |
m |
m |
|
m |
|
|||||||||
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
. (9.12) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
В частности, для вероятности попадания в симметричный относительно x m интервал справедлива формула
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
P m X m P |
X m |
|
2 |
|
|
1 2 0 |
|
|
. |
||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положив 3 , получим |
|
|
|
|
|
|
|
|
(9.13) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
P |
X m |
|
3 2 0 |
|
|
2 0 3 2 0,49865 0,9973. |
|||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это означает, что с вероятностью, близкой к единице (практически достоверно), все значения нормально распределенной СВ располагаются на интервале m 3 , m 3 . Этот факт
называют «правилом трех сигм».
Пример 4. Производят измерения напряжения на одном из выходов компьютера. Величина напряжения U является случайной, распределенной нормально с параметрами m 5 B
и 0,2 B (U N 5; 0,2 ). Найти вероятность того, что в результате испытания величина напряжения примет значение:
30
а) от 4,8 до 5,1 В; б) больше 5,2 В; в) меньше 4,7; г) отличающееся от m 5 B не более чем на 0,1 В.
Решение. а) По формуле (9.12) имеем
5,1 5 |
|
4,8 |
5 |
0 0,5 |
||||
P 4,8 X 5,1 0 |
|
|
0 |
|
|
|
|
|
0,2 |
0,2 |
|
||||||
|
|
|
|
|
|
|
||
0 1 0 0,5 0 1 0,1915 0,3413 0,5328.
б) Здесь 5,2 и . По формуле (9.12) имеем
5 |
|
|
5,2 |
5 |
|
|||
P 5,2 X 0 |
|
|
0 |
|
|
|
|
|
0,2 |
0,2 |
|
||||||
|
|
|
|
|
|
|
||
0 0 1 0,5 0,3413 0,1587.
в) Здесь 0 и 4,7. По формуле (9.12) имеем
|
P 0 X 4,7 |
|
|
4,7 5 |
0 5 |
||||||
|
0 |
|
|
0 |
|
|
|
||||
|
0,2 |
|
|||||||||
|
|
|
|
|
|
|
0,2 |
|
|||
|
0 1,5 0 25 0,4332 0,5 0,0668. |
||||||||||
|
г) По формуле (9.13) имеем |
|
|
|
|
|
|||||
|
|
|
|
0,1 |
|
|
|
|
|
||
P |
X m |
0,1 2 0 |
|
|
2 0 0,5 2 0,1915 0,383. |
||||||
|
|
||||||||||
|
|
|
|
0,2 |
|
|
|
|
|
||
|
|
9.2.4. Распределение Рэлея |
|
||||||||
|
Непрерывная неотрицательная |
случайная |
величина X |
||||||||
называется распределенной по закону Рэлея, если ее плотность распределения вероятностей имеет вид
0, |
|
|
|
если |
x 0 |
||
|
|
|
x |
2 |
|
|
|
pX x |
x |
|
|
|
(9.14) |
||
|
|
|
|||||
|
e 2 2 , если |
x 0. |
|||||
|
|||||||
2 |
|
|
|
|
|
||
Здесь 0 – параметр, характеризующий распределение. Функция распределения для закона Рэлея определяется
равенством
0, |
|
|
|
если |
x 0 |
|
|
x2 |
|
|
(9.15) |
FX x |
|
|
|
||
|
2 |
2 |
, если |
x 0. |
|
1 e |
|
|
|
Графики плотности распределения и функции распределения закона Рэлея приведены на рис. 17.
 pX(x)
pX(x)
1
e
0 |
|
x |
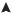 FX(x)
FX(x)
1






















1- 1
e
0 |
|
x |
Рис. 17
На практике распределение Рэлея встречается при обработке результатов стрельбы по плоской мишени (случайной величиной при этом является расстояние от центра мишени до
31 |
32 |

точки попадания), а также в некоторых задачах радиотехники и радиолокации.
НСВ X , распределенная по закону Рэлея, рассмотрена в примере 4 из занятия 8.
9.2.5. Другие распределения НСВ
1. СВ X распределена по закону равнобедренного треугольника в интервале a, a (закон Симпсона), если ее плот-
ность распределения вероятностей имеет вид, изображенный на рис. 18.
 pX(x)
pX(x)
1/a
-a |
0 |
a |
x |
Рис. 18
2. СВ X распределена по закону Коши, если
F |
x b carctg |
x |
при x . |
|
|||
X |
|
a |
|
|
|
|
3. Скорость V молекул идеального газа, находящегося в равновесии при определенной температуре, является случайной величиной, подчиняющейся закону распределения Максвелла с плотностью распределения вероятностей
|
0, |
|
|
|
|
|
|
|
|
если |
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
x |
2 |
|
|
3 2 |
|
2 |
|
|
1 |
x2 |
|
|
|
|
|
|
|
|||||||
V |
|
|
|
x |
e |
2 |
, если |
x 0, |
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где параметр распределения 0 определяется температурой
имассой молекул.
4.СВ X распределена по закону арксинуса, если
0, |
|
|
если |
x |
a |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
pX x |
|
1 |
|
, если |
|
x |
|
a. |
|
|
|
|
|
||||||
|
|
|
|||||||
|
a2 x2 |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
5. СВ X распределена по закону Лапласа с параметрами m и 0, если ее плотность распределения вероятностей
pX x |
|
1 |
|
|
e |
x m |
|
2 |
|
|
|
|
|
2 |
|
|
при x . |
||||
|
|
|
|
|||||||
2 |
||||||||||
|
|
|
|
|
|
|
||||
6. СВ X распределена по закону Парето с параметрами a 0 и x0 0, если ее функция распределения вероятностей
0, |
|
|
|
если |
x x0 |
|
x |
a |
|
|
|
FX x |
|
|
|||
1 |
|
0 |
|
, если |
x x . |
|
|||||
|
x |
|
0 |
||
|
|
|
|
|
|
В некоторых странах действует закон о налогообложении, распространяемый на тех частных предпринимателей, годовой доход которых превосходит некоторый установленный законом уровень x0 . Можно считать, что годовой доход наудачу вы-
бранного лица является случайной величиной, распределенной по закону Парето.
7. |
СВ |
X имеет гамма-распределение с параметрами |
a 0 и |
b 0 |
( X a, b ), если ее плотность распределения |
вероятностей имеет вид
33 |
34 |

0, |
|
|
|
если |
x 0 |
||
|
|
|
|
|
|
|
|
pX x ba |
|
a 1 bx |
|
|
|||
|
|
|
x |
e |
, если |
x 0, |
|
|
a |
||||||
|
|
|
|
|
|||
где a ta 1e tdt – гамма-функция Эйлера.
0
Рассмотренное в п. 9.2.2 показательное распределение с параметром является частным случаем гамма-распределения
спараметрами a 1 и b 0.
8.Другой частный случай гамма-распределения с пара-
метрами a n 2 (n – натуральное число) и b 1
2 (n – натуральное число) и b 1 2 называется
2 называется
распределением хи-квадрат с n степенями свободы (пишут
2 n ). Распределение 2 n играет большую роль в матема-
тической статистике. Если X 2 n , то ее плотность распре-
деления вероятностей имеет вид
0, |
|
|
|
|
|
если |
x 0 |
|
|
|
|
|
n |
|
x |
|
|
pX x |
1 |
|
|
1 |
|
|
||
|
|
|
|
|
|
|||
|
|
|
x2 e 2 |
, если |
x 0. |
|||
2n 2 n |
|
|||||||
|
2 |
|
|
|||||
9. СВ X подчиняется закону распределения Вейбулла с параметрами n , a и b 0, если ее плотность распределения вероятностей имеет вид
0,
|
|
|
|
|
|
|
|
pX x |
|
|
|
n x a e |
|||
b |
|
b |
|
|
|
|
|
|
|
|
|
если |
x a |
|
x a n |
|
|
||||
|
|
|
|
|
|
|
b |
, |
если |
x a. |
|||
|
|
|||||
Распределение Вейбулла в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике.
10. |
СВ |
|
X имеет |
бета-распределение с параметрами |
||
a 0 и |
b 0, |
если ее плотность распределения вероятностей |
||||
имеет вид |
a b |
|
|
|||
|
|
xa 1 |
1 x b 1, если 0 x 1 |
|||
|
|
|
|
|
||
pX x |
a b |
|
|
|||
|
|
|
||||
|
|
|
|
|
|
в остальных случаях. |
|
|
0, |
|
|||
Частным случаем бета-распределения при a b 1 является равномерное распределение на отрезке 0, 1 .
9.3.Контрольные вопросы и задания
1.Какие СВ имеют геометрическое распределение? Приведите графическое изображение геометрического распределения.
2.Какие СВ имеют биномиальное распределение? Приведите графическое изображение биномиального распределения.
3.Какие СВ имеют распределение Пуассона? Приведите графическое изображение распределения Пуассона.
4.Какие СВ имеют гипергеометрическое распределение? Приведите графическое изображение гипергеометрического распределения.
5.Приведите примеры использования рассмотренных распределений ДСВ при математическом моделировании прикладных задач.
6.Какие СВ имеют равномерное распределение? Приведите графическое изображение соответствующей плотности распределения и функции распределения.
7.Какие СВ имеют показательное распределение? Приведите графическое изображение соответствующей плотности распределения и функции распределения.
8.Какие СВ имеют нормальное распределение? Приведите графическое изображение соответствующей плотности рас-
35 |
36 |

пределения и функции распределения. В чем заключается важность нормального распределения?
9.Какие СВ имеют распределение Рэлея? Приведите графическое изображение соответствующей плотности распределения и функции распределения.
10.Приведите примеры использования рассмотренных распределений НСВ при математическом моделировании прикладных задач.
11.Разберитесь в решении задач [2], №№ 308, 328, 331, 334, 337, 346, 349, 350, 367, 369.
12.Найдите выражения для pX x и FX x СВ, распре-
деленной по закону Симпсона.
13. Вычислите коэффициенты a, b и c для FX x СВ,
распределенной по закону Коши. Найдите плотность вероятности распределения Коши.
14.Найдите функцию распределения вероятностей для закона арксинуса.
15.Пусть параметр распределения Лапласа m 0. Най-
дите функцию распределения и вычислите вероятности pk
P X k для k 1, 2, 3.
16.Найдите плотность распределения вероятностей для закона Парето.
9.4.Задачи для самостоятельной работы
1.Решите задачи [2], №№ 307, 310, 311, 312, 322, 325, 329, 330, 332, 333, 335, 336, 338, 341, 343, 348, 351, 352, 368, 370, 371.
Форма отчетности: устный опрос, контрольная работа, типовой расчет, коллоквиум, экзамен.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. М.: Высш. шк., 1998.
2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. М.: Высш. шк., 2006.
3.Вентцель Е.С. Теория вероятностей / Е.С. Вентцель. М.: Наука, 1999.
4.Кремер Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер. М.: ЮНИТИ-ДАНА, 2004.
5.Кибзун А.И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами / А.И. Кибзун, Е.Р. Горяинова, А.В. Наумов. М.: Физматлит, 2002.
6.Андронов А.М. Теория вероятностей и математическая статистика / А.М. Андронов, Е.А. Копытов, Л.Я. Гринглаз. СПб.: Питер, 2004.
7.Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике / Д.Т. Письменный. М.: Айрис-пресс, 2004.
8.Дубровская А.П. Теория вероятностей и элементы математической статистики / А.П. Дубровская, В.И. Минаков. Воронеж: ВПИ, 1993.
9.Глушко Е.Г. Элементы теории вероятностей и математической статистики / Е.Г. Глушко, А.П. Дубровская. Воронеж: ВГТУ, 2004.
10.Колемаев В.А. Теория вероятностей и математическая статистика / В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский. М.: Высш. шк., 1991.
11.Чистяков В.П. Курс теории вероятностей / В.П. Чистяков. М.: Наука, 1987.
12.Гурский Е.И. Теория вероятностей с элементами математической статистики / Е.И. Гурский. М.: Наука, 1971.
37 |
38 |
