
Использование математического моделирования при решении экономических вероятностных задач. методические указания для курсовой работы. Дежин В.В
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ВЕРОЯТНОСТНЫХ ЗАДАЧ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы по курсу
«Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения
Часть 2
A  B
B
P |
|
|
|
|
|
|
|
|
|
|
) |
( |
|
|
|
|
|
|
|
|
A |
||
|
A |
|
|
|
|
|
|
|
|
||
|
+ |
B |
|
|
|
|
|
|
( |
B |
|
|
|
) |
= |
|
|
|
|
P |
|
|
|
|
|
P(A |
|
|
)- |
|
|
|
|||
|
|
|
|
B |
|
|
|
|
|||
|
|
|
|
P( |
|
|
|
|
|
||
|
|
|
|
|
)+ |
|
|
|
|
|
|
Воронеж 2013
Составитель канд. физ.-мат. наук В.В. Дежин
УДК 517 Использование математического моделирования при ре-
шении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 2 / ФГБОУВПО «Воронежский государственный технический университет»; сост. В.В. Дежин. Воронеж, 2013. 32 с.
Методические указания предназначены в качестве руководства для самостоятельного изучения студентами направления 080100 «Экономика» профиля «Экономика предприятий и организаций» (Э) очной формы обучения курса «Теория вероятностей и математическая статистика». Методические указания включают в себя 3 занятия и содержат основные понятия, ссылки на литературу, пояснения и примеры, контрольные вопросы и задачи, форму отчетности.
Предназначены для студентов третьего семестра второго курса.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле Э-ТВиМС-2.pdf.
Ил. 1. Библиогр.: 19 назв.
Рецензент канд. физ.-мат. наук, доцент А.Н. Шелковой Ответственный за выпуск зав. кафедрой д-р физ.-мат. на-
ук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУВПО «Воронежский государственный технический университет», 2013
2

Занятие № 4
УСЛОВНЫЕ ВЕРОЯТНОСТИ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
4.1. Основные понятия
Пусть A и B – наблюдаемые события в эксперименте, причем P B 0. Условной вероятностью P A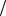 B PB A
B PB A
осуществления события A при условии, что событие B произошло в результате данного эксперимента, называется величина, определяемая равенством
P A B |
P AB |
. |
(4.1) |
|
|||
|
P B |
|
|
Для краткости условную вероятность P A B |
называют «ве- |
||
роятностью события A при условии B ». Нетрудно проверить, что в случае произвольного вероятностного пространства определенная формулой (4.1) вероятность P A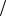 B , рассматри-
B , рассматри-
ваемая как функция наблюдаемых событий A при фиксированном событии B , удовлетворяет трем основным аксиомам вероятностей (см. занятие № 3). Формула (4.1), по существу, сводит вопрос о вычислении условной вероятности к вычислению двух безусловных вероятностей.
Событие A называется независимым от события B , удовлетворяющего условию P B 0, если выполняется ра-
венство P A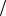 B P A . События A и B называются незави-
B P A . События A и B называются незави-
симыми, если
P AB P A P B . |
(4.2) |
События A1, A2, , An называются независимыми в совокуп-
ности, если для любого набора из m событий (m 2, 3, , n) выполняется равенство
P Ak1 Ak2 Akm P Ak1 P Ak2 P Akm , |
km 1, 2, , n . |
|
(4.3) |
Формулы (4.2) и (4.3) позволяют выделять независимые события в тех случаях, когда модель вероятностного эксперимента формализована и вероятности всех нужных событий полностью определены. Однако в практических задачах, связанных с проведением реальных экспериментов, далеко не всегда возможно использование данных критериев независимости. В таких случаях часто применяют гипотезу о физической независимости событий: считаются независимыми события, не связанные причинно. Так, например, естественно считать независимыми события, связанные с появлением брака определенного вида изделий, производимых двумя поточными линиями на различных предприятиях.
Сложным событием называется наблюдаемое событие, выраженное через другие наблюдаемые в том же эксперименте события с помощью допустимых алгебраических операций. Вероятность осуществления того или иного сложного события вычисляется по правилам, основу которых составляют:
– формула умножения вероятностей
P AB P A P B A P B P A B , |
(4.4) |
– формула сложения вероятностей |
|
P A B P A P B P AB . |
(4.5) |
Формула (4.4) справедлива, если P A 0, P B 0, и позво-
ляет вычислять вероятность совместного осуществления событий A и B в тех случаях, когда условная вероятность считается известной (из дополнительных опытов) или определяется методом вспомогательного эксперимента.
Формулы умножения и сложения для произвольного чис-
ла событий записываются следующим образом:
P A1A2 An P A1 P A2 |
A1 P An |
A1A2 An 1 , (4.6) |
2

|
n |
|
|
|
n |
k |
|
|
|
i |
j |
|
|
k |
|
|
|
P |
|
||||||
P |
|
A |
|
|
P A |
|
A A |
|
||||
k 1 |
|
|
|
k 1 |
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
(i j) |
|
|
|
|
P AiAj Ak 1 n 1 P A1A2 An . (4.7)
i j k (i j k)
В частности, для трех событий имеем:
P ABC P A P B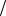 A P C
A P C AB ,
AB ,
P A B C P A P B P C
P AB P AC P BC P ABC .
В случае трех и большего числа событий для нахождения вероятности суммы S этих событий проще найти вероятность
противоположного события S , а затем воспользоваться равенством P S 1 P S .
Аксиома 3 (занятие № 3) дает правило вычисления веро-
|
|
|
|
|
k |
|
|
k |
|
. |
|||
ятности суммы несовместных событий P |
A |
|
|
P A |
||
|
k |
|
|
k |
|
|
4.2. Примеры решения задач
Пример 1. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, на втором три. Найти вероятность того, что все детали первосортные.
Решение. Пусть событие Ak (k 1, 2) означает, что k -я деталь, изготовленная на первом станке, будет первосортной, а событие Bn (n 1, 2, 3) означает, что n-я деталь, изготовлен-
ная на втором станке, будет первосортной. Тогда искомая вероятность равна вероятности одновременного наступления
этих событий p P A1A2B1B2B3 . Так как рассмотренные со-
бытия независимы в совокупности, то
p P A1 P A2 P B1 P B2 P B3 0,72 0,83 0,251.
Пример 2. Вероятности того, что любая деталь окажется бракованной в результате механической и термической обработки, равны соответственно p1 и p2 . Вероятности того, что брак является неустранимым, соответственно равны p3 и p4 .
Определить:
а) какое количество деталей необходимо взять после механической обработки, чтобы с вероятностью 0,9 можно было утверждать, что хотя бы одна из них будет сдана доброкачественной в термическую обработку с учетом возможности устранения брака;
б) вероятность того, что хотя бы одна из трех деталей будет иметь неустранимый брак после прохождения сначала механической, а затем термической обработки.
Решение. а) Пусть событие A {хотя бы одна из n деталей будет сдана доброкачественной в термическую обработку с учетом возможности устранения брака}. Рассмотрим противоположное событие A {все n деталей будут сданы в термиче-
скую обработку с неустранимым браком}, |
тогда P A |
||||
1 P |
|
. Очевидно |
|
B1B2 Bi Bn , где |
событие Bi |
A |
A |
||||
={i-я деталь будет сдана в термическую обработку с неустранимым браком}. Так как каждая деталь проходит механическую обработку независимо, то события Bi независимы и
P A P B1 P B2 P Bn . Каждое событие Bi , в свою очередь, является произведением двух событий: C1 {деталь ока-
залась бракованной |
после термической обработки} и |
C2 {брак является |
неустранимым}, поэтому P Bi |
3 |
4 |
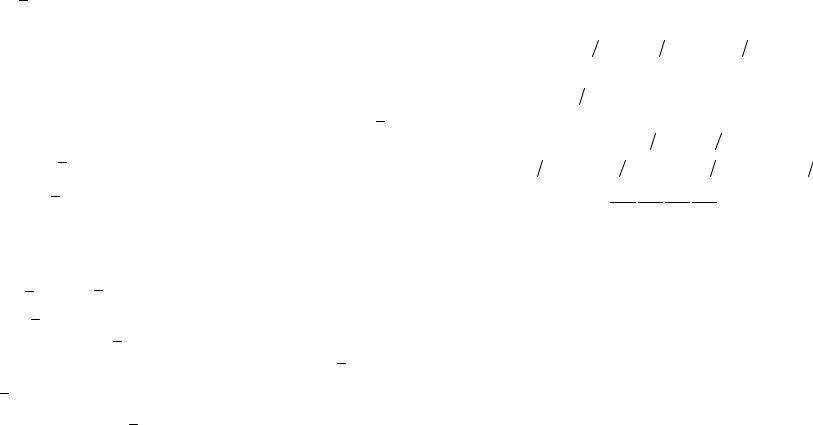
P C1C2 P C1 P C2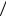 C1 p1p3 . Таким образом P A1 P A 1 P B1 P B2 P Bn 1 p1p3 n . По условию
C1 p1p3 . Таким образом P A1 P A 1 P B1 P B2 P Bn 1 p1p3 n . По условию
P A 0,9, тогда p1p3 n 0,1. Логарифмируя, получаем
n 1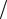 lg p1p3 .
lg p1p3 .
б) Пусть событие A {хотя бы одна из трех деталей будет иметь неустранимый брак после механической и термиче-
ской обработки}. Рассмотрим противоположное событие A ={ни одна из деталей не имеет неустранимого брака}, тогда
P A 1 P A . Так как детали проходят обработку незави-
симо, то P A P BC 3, где независимые события B {де-
таль не имеет брака или его устранили после механической обработки} и C {деталь не имеет брака или его устранили после термической обработки}. Получаем P BC P B P C
1 P B 1 P C . Здесь использованы противоположные
события B {после механической обработки деталь имеет не-
устранимый брак} и C {после термической обработки деталь имеет неустранимый брак}, их вероятности равны P B p1p3
и P C p2 p4 (см. пункт а). Таким образом
P A 1 P A 1 1 p1p3 3 1 p2 p4 3.
Пример 3. Производитель поставил потребителю 200 изделий, среди которых 2 % неисправных. Потребитель решил провести выборочный контроль четырех изделий, при этом условием отказа от всей партии является наличие хотя бы одного неисправного изделия среди проверяемых. Какова вероятность возврата изделий производителю?
Решение. Найдем вероятность q противоположного события A, которое заключается в том, что партия будет приня-
та. Событие |
A является произведением четырех |
событий: |
||
A A1A2A3A4, |
где Ai (i 1, 2, 3, 4) означает, |
что i-е изделие |
||
доброкачественное. События Ai зависимые, |
поэтому P A |
|||
P A1 P A2 |
A1 P A3 A1A2 P A4 A1A2A3 . |
Всего |
изделий |
|
200, а |
исправных среди них 200 0,02 200 196, |
поэтому |
||
P A1 |
196 200. После осуществления события A1 |
останется |
||
199 изделий, среди которых 195 исправных, поэтому условная
вероятность |
P A2 |
A1 195 199. |
Аналогично |
имеем |
P A3 A1A2 |
194 198 |
и P A4 A1A2A3 193 197. Таким обра- |
||
зом q P A 196 195194193 0,922. Искомая вероятность
200199198197
равна p 1 q 0,078.
Пример 4. В партии из n деталей m бракованных. Для проверки наудачу выбирают s изделий. Партия бракуется, если среди выбранных изделий более k бракованных (k s). Определить вероятность того, что партия будет забракована.
Решение. Пусть Ai – событие, состоящее в том, в вы-
бранных s изделиях i бракованных (i k 1, k 2, , s). Интересующее нас событие можно представить в виде суммы несовместных событий: Ak 1 Ak 2 As . Отсюда искомая вероятность p P Ak 1 Ak 2 As P Ak 1 P Ak 2
P As . Найдем вероятность события Ai . Из n изделий s
можно выбрать Cns |
способами, из m бракованных изделий i |
|||||||
можно выбрать Ci |
способами, остальные |
s i |
исправных из- |
|||||
m |
|
|
|
|
|
|
|
|
делий можно выбрать из всех n m исправных Cns mi |
способа- |
|||||||
|
|
Ci |
Cs i |
|
1 |
|
s |
s i |
|
|
m n m |
|
|
|
i |
||
ми. Таким образом |
P Ai |
|
|
и p |
|
CmCn m . |
||
|
Cs |
Cs |
||||||
|
|
|
n |
|
n i k 1 |
|
||
5 |
6 |

Пример 5. Отбор новых изделий для постановки на производство проводит комиссия из трех человек. Первый и второй принимают верное решение независимо друг от друга с вероятностью p , а третий участник комиссии поступает следующим образом: 1) для принятия решения бросает монету; 2) если два первых участника комиссии принимают одинаковые решения, то он к ним присоединяется, если же решения двух первых разные, то третий бросает монету. Окончательное решение комиссия принимает по большинству голосов. Какова в каждом случае вероятность того, что комиссия примет верное решение?
Решение. Пусть события A1, A2 и A3 – принятие верно-
го решения первым, вторым и третьим участником комиссии соответственно. Вероятность принятия верного решения третьим участником по результату падения монеты равна 1 2.
2.
Рассмотрим первый и второй случаи. |
|
|
|
|
||||||
1) |
Введем |
события: |
B1 A1A2A3 |
{все три |
участника |
|||||
приняли |
верное |
решение}, |
B2 A1A2 |
|
|
и второй |
||||
A3 {первый |
||||||||||
приняли |
верное |
решение, |
а третий |
– ошибочное}, |
B3 |
|||||
A1 |
|
2A3 |
{первый и третий приняли верное решение, |
а вто- |
||||||
A |
||||||||||
рой – ошибочное}, B4 A1A2A3 {второй и третий приняли
верное решение, а первый – ошибочное}. Рассматриваемое событий (комиссия примет верное решение) заключается в наступлении одного из событий Bi (i 1, 2, 3, 4). События Bi
несовместны, а события A1, A2 и A3 независимые, поэтому искомая вероятность будет равна
P B1 B2 B3 B4 P B1 P B2 P B3 P B4
P A1A2A3 P A1A2A3 P A1A2A3 P A1A2A3
P A1 P A2 P A3 P A1 P A2 P A3
P A1 P A2 P A3 P A1 P A2 P A3pp 1 pp 1 p 1 p 1 1 p p 1
2 |
2 |
2 |
2 |
1 p p p 1 p 1 p p . 2
2) Введем события: C1 A1A2A3 {первый и второй при-
няли верное решение, а третий к ним присоединился}, C2
A1A2A3 {первый принял ошибочное решение, второй – вер-
ное, а третий – верное по результату падения монеты}, C3
A1A2A3 {первый принял верное решение, второй – ошибоч-
ное, а третий – верное по результату падения монеты}. Рассматриваемое событие заключается в наступлении одного из событий C1, C2, C3 . Эти события несовместны, поэтому иско-
мая вероятность равна
P C1 C2 C3 P C1 P C2 P C3
P A1A2A3 P A1A2A3 P A1A2A3
P A1 P A2 P A3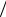 A1A2 P A1 P A2 P A3
A1A2 P A1 P A2 P A3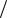 A1A2
A1A2
P A1 P |
|
2 P A3 |
A1 |
|
2 |
p p 1 1 p p |
1 |
|
|
A |
A |
||||||||
|
|||||||||
|
|
|
|
|
|
2 |
|
||
p 1 p 1 p2 1 p p p . 2
Пример 6. На предприятие поступила партия изделий в количестве 1000 штук. Из этих изделий 50 имеют повреждения окраски, на 40 имеются зазубрины и на 30 имеются вмятины, 20 изделий имеют зазубрины и повреждения окраски, 10 изделий имеют вмятины и повреждения окраски, 8 изделий имеют зазубрины и вмятины, 3 изделия имеют все три вида повреждений. Наудачу выбирается одно изделие для проверки. Определить вероятности следующих событий: A {выбранное из-
7 |
8 |

делие имеет повреждение окраски или вмятины}, B {выбранное изделие не имеет повреждений}.
|
|
C |
|
|
|
|
|
|
|
|
D |
|
|
|
50 |
|
20 |
|
40 |
||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
10 |
8 |
|
|
|
||||
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|||
Решение. |
|
Рассмотрим |
|
следующие события: C {вы- |
|||||||
бранное изделие имеет повреждения окраски}, D {выбранное |
|||||||||||
изделие имеет |
|
зазубрины}, |
|
E {выбранное изделие имеет |
|||||||
вмятины}. Из условия задачи видно, что события C, D, E со- |
|||||||||||
вместны (рис. 1). Получаем |
|
|
|
|
|
|
|||||
P A P C E P C P E P CE |
|||||||||||
|
|
50 |
|
30 |
|
|
10 |
|
|
70 |
0,07. |
1000 |
|
1000 |
1000 |
||||||||
|
1000 |
|
|
|
|||||||
Для вычисления вероятности события B CDE используем правила де Моргана и формулу сложения для трех совместных событий:
P B P CDE P C D E 1 P C D E
1 P C P D P E P CD P CE P DE
P CDE 1 |
50 |
|
|
|
40 |
|
|
30 |
|
|
|
20 |
|
|
10 |
|
||||||
|
|
|
|
1000 |
|
|
|
|
1000 |
1000 |
||||||||||||
1000 |
|
|
1000 |
|
|
|
||||||||||||||||
|
8 |
|
|
|
3 |
|
|
1 |
|
85 |
|
0,915. |
|
|
|
|||||||
|
|
|
|
|
|
|
1000 |
|
|
|
|
|||||||||||
1000 |
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 7. В продукции завода брак составляет 5 % от общего количества выпускаемых деталей. Для контроля отобрано 20 деталей. Какова вероятность того, что среди них имеется хотя бы одна бракованная?
Решение. Для любой детали из продукции завода вероятность быть бракованной равна по условию p P Ak 0,05 (k 1, 2, , 20), где событие Ak {k -я по счету извлеченная деталь бракованная}. Рассматриваемому событию соответствует сумма совместных событий A1 A2 A20 . В условиях отлаженного технологического процесса можно считать, что события A1, A2, , A20 независимы в совокупности. Учитывая вышеизложенное и пользуясь правилом де Моргана, получаем
P A1 A2 A20 1 P A1 A2 A20
20
1 P A1A2 A20 1 P Ak 1 p20 1 0,0520 0,64 .
k1
4.3.Контрольные вопросы и задания
1.Что такое условная вероятность события?
2.Когда два события являются независимыми?
3.Какие события называются независимыми в совокуп-
ности?
4.Следует ли из попарной независимости событий их независимость в совокупности? Приведите примеры.
5.Пусть события A и B независимы. Будут ли тогда не-
зависимы и события A и B? Обосновать ответ.
9 |
10 |
6.Какие события являются совместными и какие несовместными?
7.Будут ли зависимы два несовместных события с ненулевыми вероятностями? Обосновать ответ.
8.Будут ли два независимых события с ненулевыми вероятностями совместными? Обосновать ответ.
9.Пусть события A и B зависимы. Следует ли из этого, что они несовместны? Привести примеры.
10.Какое событие называется сложным?
11.Запишите формулы сложения и умножения вероятностей для двух событий.
12.Запишите формулы сложения и умножения вероятностей для произвольного числа событий.
13.Запишите формулу умножения вероятностей для независимых событий.
14.Запишите формулу сложения вероятностей для несовместных событий.
15.Объясните отличие примеров 3 и 7.
4.4.Задачи для самостоятельной работы
1.Решите задачи №№ 47, 50, 53, 55, 57, 62, 65, 67, 69, 81, 83, 87 [2].
2.Имеются 8 заказов на отправку товара внутри страны и 6 – на экспорт. Какова вероятность того, что из двух выбранных наудачу заказов последний будет предназначен для экспорта?
3.Совет директоров состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Планируется создать подкомитет из трех его членов. Вероятность войти в подкомитет одинакова для любого члена совета директоров. Какова вероятность того, что в подкомитет попадут только бухгалтеры?
Форма отчетности: устный опрос, типовой расчет, экза-
мен.
Занятие № 5
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА
5.1. Основные понятия
Пусть событие A может произойти с одним и только одним из попарно несовместных событий H1, H2, , Hn , обра-
|
n |
P H |
|
|
зующих полную группу |
|
k |
1 и удовлетворяющих |
|
|
|
|
||
k 1 |
|
|
|
|
условию P Hk 0 (k 1, 2, , n). Тогда справедлива форму-
ла полной вероятности:
n
P A P Hk P A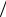 Hk .
Hk .
k 1
События Hk принято называть гипотезами по отношению к событию A. Безусловные вероятности P Hk трактуются как
доопытные (априорные) вероятности гипотез. В ряде случаев выбор системы гипотез не определяется однозначно условиями эксперимента. В таких случаях предпочтение следует отдавать той системе, для которой условные вероятности вычисляются наиболее просто. Формула полной вероятности позволяет определить вероятность осуществления события A с учетом возможности наступления любой из гипотез.
Пусть события A, H1, H2, , Hn удовлетворяют условиям формулы полной вероятности и P A 0. Пусть экспери-
мент проведен и стало известно, что событие A осуществилось. Какова послеопытная (апостериорная) вероятность осуществления гипотезы Hk при условии, что событие A имело место? Ответ дается формулой Байеса
11 |
12 |
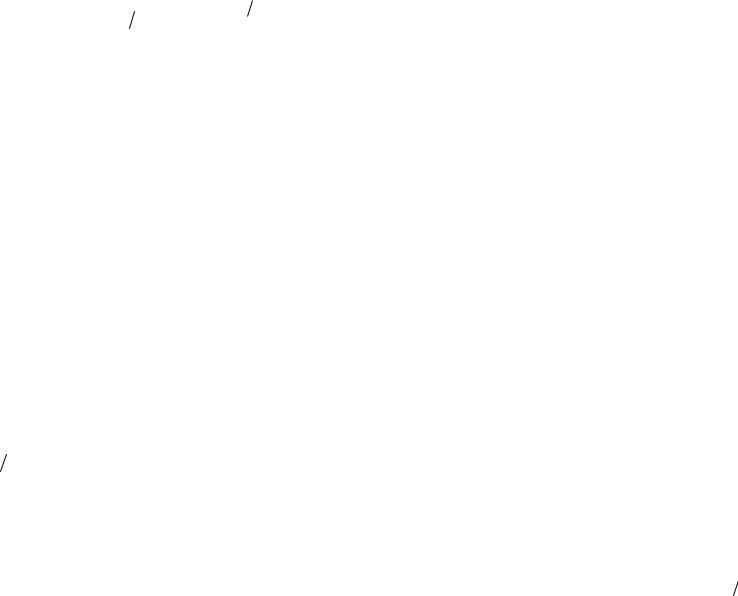
P Hk |
A |
P Hk P A Hk |
, |
|
P A |
||||
|
|
|
||
n |
|
|
|
где P A P Hk P A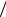 Hk – полная вероятность осущест-
Hk – полная вероятность осущест-
k 1
вления события A. Формула Байеса позволяет «переоценить» вероятность каждой из гипотез после поступления новой информации относительно осуществления тех или иных наблюдаемых событий. Особое значение приобретает формула Байеса для таких экспериментов, в которых гипотезы Hk непо-
средственно не наблюдаемы, хотя априорные вероятности P Hk и соответствующие условные вероятности P A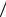 Hk
Hk
известны из дополнительных опытов. Такая ситуация может иметь место, например, если отсутствует прибор, позволяющий регистрировать факт осуществления данных гипотез, или же если применение прибора для регистрации осуществления гипотез приводит к разрушению предмета наблюдения (разрушающий контроль). Для подобных экспериментов переоценка вероятностей гипотез после опыта может быть проведена на основании наблюдаемого события A, тесно связанного с гипотезами. Такой подход часто используется в задачах медицинской и технической диагностики. В экономике априорные ве-
роятности |
P Hk и соответствующие условные вероятности |
P A Hk |
часто определяют, пользуясь известными из преды- |
дущей практики сведениями, проводят исследования рынка.
5.2. Примеры решения задач
Пример 1. Имеются две партии изделий по 20 и 12 штук, причем в первой партии 15 изделий доброкачественных и 5 бракованных, а во второй 8 доброкачественных и 4 бракованных. Из первой партии наудачу выбрали 3 изделия и переложили во вторую партию. После этого наудачу выбирается одно
изделие из второй партии. Определить вероятность того, что оно доброкачественное.
Решение. Пусть событие A {извлечение доброкачественного изделия из второй партии}. Этому событию предшествует перемещение трех изделий из первой партии во вторую. Являются ли эти 3 изделия бракованными или доброкачественными неизвестно, поэтому делаем следующие предположения (гипотезы) о составе переложенных изделий: H1 {пере-
ложили 3 доброкачественных изделия}, H2 {переложили 2
доброкачественных изделия и 1 бракованное}, H3 {перело-
жили 1 доброкачественное изделие и 2 бракованных}, H4 {переложили 3 бракованных изделия}. Очевидно, что других гипотез выдвинуть нельзя. Также видно, что выдвинутые гипотезы являются попарно несовместными событиями. Вычисляем вероятности гипотез по формуле классической вероятности с использованием числа сочетаний:
P H1 |
C3 C0 |
|
|
15! 3!17! |
|
|
|
13 14 15 |
|
||||||||||||||||||
|
15 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
0,399; |
||||||||||||
|
|
C203 |
|
3!12! 20! |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
18 19 20 |
|
|||||||||||||
P H2 |
|
C2 C1 |
|
|
|
15! 3!17! 5 |
|
14 15 3 5 |
|
||||||||||||||||||
|
|
|
15 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,461; |
|||||||||
|
|
C203 |
|
|
|
2!13! 20! |
18 19 20 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
P H3 |
|
|
C1 C2 |
|
|
|
15 3!17! 5! |
|
|
15 3 4 5 |
|
||||||||||||||||
|
|
15 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,132; |
||||||||||
|
C203 |
|
|
|
|
|
20! 2 3! |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 19 20 |
|
|||||||||
P H4 |
|
C0 |
C |
3 |
|
|
|
|
3!17! 5! |
|
|
|
|
|
3 4 5 |
|
|||||||||||
|
15 5 |
|
|
|
|
|
|
|
|
|
|
0,009. |
|||||||||||||||
|
|
20! 3! 2! |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
C203 |
|
|
|
|
|
|
|
|
18 19 20 |
|
|||||||||||
Проверка: 0,399+0,461+0,132+0,009=1,000. Вероятность того,
что из второй партии будет извлечено доброкачественное из-
делие, при условии, |
что в нее переложили 3 доброкачествен- |
||||
ных изделия, будет |
равна P A H1 |
8 3 |
|
0,733. Здесь в |
|
12 3 |
|||||
|
|
|
|||
знаменателе прибавили 3, так как во вторую партию перело-
13 |
14 |

жили 3 изделия, а в числителе прибавили 3, так как переложили 3 доброкачественных изделия. Аналогично вычисляются
остальные |
условные вероятности: |
P A H2 |
8 2 |
|
0,667; |
|||||
|
|
|||||||||
|
8 1 |
|
|
|
8 0 |
|
12 3 |
|||
P A H3 |
0,600; |
P A H4 |
0,533. |
Искомую |
||||||
12 3 |
12 3 |
|||||||||
|
|
|
|
|
|
|
|
|||
вероятность находим по формуле полной вероятности:
P A P H1 P A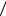 H1 P H2 P A
H1 P H2 P A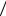 H2 P H3 P A
H2 P H3 P A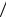 H3
H3
P H4 P A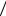 H4 0,399 0,733 0,461 0,667
H4 0,399 0,733 0,461 0,667
0,132 0,600 0,009 0,533 0,683.
Пример 2. Имеются две партии изделий по 50 и 40 штук, причем известно, что в первой партии 5 изделий с дефектами, а во второй партии 10 изделий с дефектами. Изделие, взятое из наудачу выбранной партии, оказалось с дефектами. Определить вероятность того, что второе изделие, выбранное наудачу из этой же партии, окажется без дефектов.
Решение. Пусть событие A {первое изделие имеет дефекты}, а событие B {второе изделие не имеет дефектов}. Можно сделать две гипотезы: H1 {изделия взяты из первой
партии}, H2 {изделия взяты из второй партии}. |
P H1 |
|
P H2 0,5, так как выбор любой из партий равновероятен. |
||
По условию P A H1 5 50 0,1; |
P A H2 10 |
40 0,25. |
Вероятность события A находим по формуле полной вероят-
ности: P A P H1 P A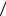 H1 P H2 P A
H1 P H2 P A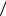 H2 0,5 0,1
H2 0,5 0,1
0,5 0,25 0,175. Вероятности гипотез H1 и H2 следует переоценить, так как произошло испытание (событие A). Определяем их новые значения по формуле Байеса:
P H1 |
A |
P H1 P A H1 |
|
0,5 0,1 |
0,286 ; |
P A |
|
||||
|
|
0,175 |
|
||
|
P H2 |
A |
P H2 P A H2 |
|
0,5 0,25 |
0,714. |
|
||
|
|
|
|
||||||
|
|
|
P A |
|
0,175 |
|
|
||
Вероятность события B находим по формуле полной вероят- |
|||||||||
ности. |
По |
условию |
задачи |
|
P B H1 45 49 0,918; |
||||
P B H2 30 |
39 0,769. |
В качестве вероятностей |
гипотез |
||||||
следует |
взять переоцененные |
вероятности P H1 |
A и |
||||||
P H2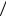 A , поэтому
A , поэтому
P B P H1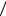 A P B
A P B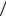 H1 P H2
H1 P H2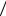 A P B
A P B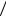 H2
H2
0,286 0,918 0,714 0,769 0,812 .
Пример 3. На производственном участке установлены 4 независимо работающих станка, изготовленных на разных заводах. Вероятности поломки станков, выпускаемых первым, вторым, третьим и четвертым заводом, равны, соответственно, p1, p2 , p3 и p4 . По истечении некоторого времени три станка
вышли из строя. Найти вероятность того, что исправным остался станок, изготовленный вторым заводом.
Решение. Возможна следующая полная система гипотез
о работоспособности станков: |
H0 {все станки |
исправны}, |
H1 {один станок неисправен, |
а три исправны}, |
H2 {два |
станка неисправны и два исправны}, H3 {станки, выпущен-
ные первым, вторым и третьим заводами неисправны, а станок,
выпущенный |
четвертым заводом |
исправен} или |
кратко |
H3 {1, 2, 3 – неисправны, 4 – исправен}, H4 {1, 2, 4 – неис- |
|||
правны, 3 – исправен}, H5 {1, 3, 4 – неисправны, 2 – испра- |
|||
вен}, H6 {2, |
3, 4 – неисправны, 1 |
– исправен}, H7 {все |
|
станки неисправны}. Произошло событие A {три станка вы- |
|||
шли из строя}. Определим условные вероятности события A |
|||
при каждой гипотезе. Видно, что при гипотезах H0 , |
H1, H2, |
||
15 |
16 |

H7 событие A невозможно и условные вероятности
P A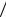 H0 P A
H0 P A H1 P A
H1 P A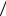 H2 P A
H2 P A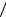 H7 0. При гипотезах
H7 0. При гипотезах
H3, H4, H5, H6 событие A достоверно и условные вероятно-
сти P A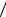 H3 P A
H3 P A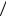 H4 P A
H4 P A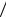 H5 P A
H5 P A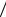 H6 1. Вероятно-
H6 1. Вероятно-
сти гипотез определяем по теореме умножения для независи-
мых |
событий: P H3 p1p2 p3 1 p4 p1p2 p3q4 , |
P H4 |
p1p2q3p4 , P H5 p1q2 p3p4 , P H6 q1p2 p3p4 . |
Таким об- |
|
разом |
P A p1p2 p3q4 p1p2q3p4 p1q2 p3p4 q1p2 p3p4. Ис- |
|
комую вероятность исправности станка, изготовленного вторым заводом, при условии, что вышли из строя три станка, оп-
ределяем по формуле Байеса: P H5 |
A |
P H5 P A H5 |
|
||
|
P A |
||||
|
|
|
|
|
|
|
p1q2 p3p4 |
|
. |
|
|
|
|
|
|||
p1p2 p3q4 p1p2q3p4 p1q2 p3p4 q1p2 p3p4
Пример 4. Для поиска месторождений нефти на заданной территории нефтяной компанией было организовано n геологоразведочных партий, каждая из которых независимо от других обнаруживает залежь нефти с вероятностью p . После обработки и анализа сейсмографических записей вся территория была поделена на два района. В первом районе нефть может залегать с вероятностью p1, а во втором – с вероятностью
1 p1. Как следует распределить n геологоразведочных партий по двум районам, чтобы вероятность обнаружения нефти была максимальной?
Решение. В задаче требуется определить вероятность события A {хотя бы одна из n геологоразведочных партий обнаружила нефть}. Найдем вероятность обратного события
A {ни одна из n геологоразведочных партий не обнаружила нефть}. Эта вероятность находится по формуле полной веро-
ятности P |
A |
P H1 P |
A |
H1 P H2 P |
A |
H2 , |
где введе- |
||||||||
ны гипотезы |
H1 {залежь |
залегает в первом |
районе}, |
||||||||||||
H2 {залежь |
залегает во |
втором районе}. По |
условию |
||||||||||||
P H1 p1, |
P H2 1 p1. Пусть в первом районе производят |
||||||||||||||
поиск нефти |
|
m геологоразведочных партий, тогда во втором |
|||||||||||||
районе будет |
n m геологоразведочных партий. P |
|
H1 – |
||||||||||||
A |
|||||||||||||||
вероятность того, что |
m партий, посланных в первый район, |
||||||||||||||
не обнаружат нефть; |
P |
|
H2 – вероятность того, |
что n m |
|||||||||||
A |
|||||||||||||||
партий, посланных во второй район, не обнаружат нефть. По
теореме умножения для независимых событий |
P |
A |
H1 |
||||||
1 p m и |
P |
|
H2 1 p n m . Таким |
образом |
P A |
||||
A |
|||||||||
1 P |
|
1 p1 1 p m 1 p1 1 p n m |
Нам |
необходимо |
|||||
A |
|||||||||
установить значение m, при котором вероятность |
P A мак- |
||||||||
симальна, т.е. имеем задачу определения точки максимума функции f x 1 p1 1 p x 1 p1 1 p n x . Находим производную и приравниваем ее к нулю:
f x p1 1 p x ln 1 p 1 p1 1 p n x ln 1 p 0.
Отсюда p |
1 p 2x n 1 p и x |
max |
|
n |
|
1 |
ln |
1 p1 |
ln 1 p . |
1 |
1 |
2 |
2 |
|
p |
|
|||
|
|
|
|
|
|
|
1 |
|
|
Для проверки того, что точка xmax является точкой максимума,
находим вторую производную
f x ln2 1 p p1 1 p x 1 p1 1 p n x .
Из полученного выражения видно, что f x 0 |
при 0 p 1 |
и 0 p1 1, поэтому xmax действительно является точкой мак-
симума f x . Таким образом в первый район следует послать
17 |
18 |
