Учебники 8070

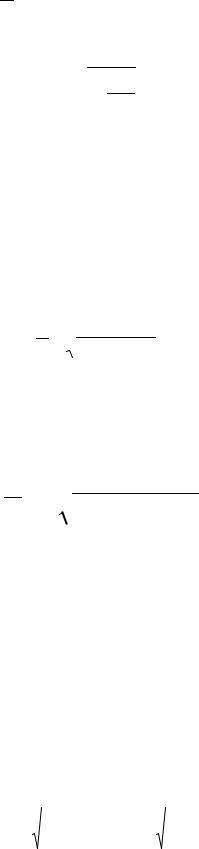
Q= M i

imi

Подставляя найденное значение mi в выражение для расчета среднего удельного расхода то есть m , получаем

n

∑Mi

m = in=1 M .

∑ i

i=1 mi

Таким образом, средний удельный расход материала вычисляется по средней гармонической взвешенной, в которой в качестве доли признака используется количество материала Mi, а осредняемым признаком является mi.

Из всего спектра средних степенных особое место занимает средняя геометрическая, которую применяют в тех случаях, когда объем совокупности формируется не суммой, а произведением индивидуальных значений признаков. Этот вид средней используется для вычисления средних коэффициентов (темпов) роста в рядах динамики. Так, в случае одинаковых временных интервалов между и уровнями динамического ряда средняя геометрическая простая имеет такой вид:

K = m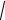K1K2 Km

уровни ряда; т – количество темпов роста (т = п – 1).

Если временные интервалы между и уровнями динамического ряда неравны, то используется средняя геометрическая взвешенная

m

K = ∑i=1 fi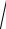K1f1 K2f2 Kmfm

Подчеркнем особенности использования данной формулы: если исходный ряд динамики содержит n уровней ряда, то по этим данным можно вычислить темпы роста только за (n – 1) периодов. Таким образом, для базисного, как правило начального, уровня темп роста не вычисляется из-за недостаточности исходных данных. Это обстоятельство позволяет ряд динами условно разбить на две части: базисный период и изучаемый период (все уровни динамического ряда кроме первого). Обозначив число уровней ряда составляющих изучаемый период через m и приходим к приведенной выше формуле.

Следует отметить, что данная формула расчета средних темпов роста в рядах динамики имеет достаточно существенный недостаток. Если в формулу простой средней геометрической подставить значения цепных темпов роста, то получим

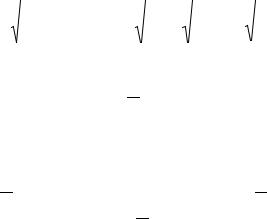
то есть при вычислении среднего темпа роста используется только конечный и начальный уровень ряда динамики, влияние же остальных значений в данном случае учитываться не будет. Это обстоятельство послужило основой для того факта, что в теории статистики данный способ расчета средних темпов роста не считается универсальным, так как очень часто необходимо контролировать темпы роста по каждому периоду, что при подобном способе расчета сделать будет уже невозможно, так как использование среднего тепа роста, рассчитанного по данной формуле будет давать искаженный результат. Данный факт иллюстрирует следующий пример.

Рассмотрим расчет темпов роста характеризующих динамику объемов работ (в млрд. рублей), выполненных собственными силами, по виду деятельности «Строительство», в Воронежском регионе за последние пять лет. Соответствующие данные приведены в табл. 1.

Таким образом суммарный объем выполненных строительных работ за последние пять лет в Воронежском регионе составил 296,6 млрд. руб.

Понятно, что данный динамический ряд делится на две расти: за базисный уровень приятны данные 2010 года, а изучаемый период составляет 4 года: 2011, 2012, 2013, 2014. Таким образом, в данной задаче m=4.

Находим средний темп роста

Теперь можно проверить, что уровень 2014 года может быть определен по формуле

y2014 = y2010 K 4 = 40,8 1,116784 = 75,9 ,

и составляет фактическую величину, достигнутую в этом году.

Однако, если использовать данное среднее значение темпа роста для других уровней динамического ряда, то получим следующее:

y2013 = y2010 K3 = 40,8 1,116783 = 65, y2012 = y2010 K 2 = 40,8 1,116782 =55,7,

y2011 = y2010 K = 40,8 1,11678 = 47,7.

Теперь найдем общий объем произведенных работ в Воронежском регионе за последние пять лет с использованием полученного значения среднего темпа роста. Получим

75,9+65+55,7+47,7+40,8=285 млрд. руб.

Таким образом отклонение фактического объема выполненных работ от объемов работ, полученных расчетным путем составляет 11,6 млрд. руб. или 3,9% от базисного периода за который принят 2010 год. Такое отклоне-

14

ние стало возможным из-за особенностей расчета среднего темпа роста, когда используются только два значения из всего рада динамики: первое и последнее.

Попробуем применить алгоритм выбора средней степенной величины к данной задаче.

1.Определяем цель и задачи вычисления средней величины. Понятно, что в данном случае задача заключается в получении такой средней величины, которая максимально точно отражала бы данные об объеме выполненных работ как за весь анализируемый период, так и отдельно по годам.

2.Исходя из цели и задач выбираем определяющий показатель и формулу его расчета. В данном случае в качестве определяющего показателя принимается объем выполненных работ за весь анализируемый период, то есть

n

Q = ∑ yi = y0 + y1 + y2 +...+ yn ,

i=0

или применительно к нашим исходным данным получаем

Q = y2010 + y2011 + y2012 + y2013 + y2014 = y2010 + K1 y2010 + K2 y2011 + K3 y2012 + K4 y2013 .

ем

Q= y2010 + K1 y2010 + K2 K1 y2010 + K3 K2 K1 y2010 + K4 K3 K2 K1 y2010 .

3.Выбираем вид средней степенной величины исходя из правила: значение определяющего показателя не должно измениться при замене индивидуальных значений признака на среднее значение. В этом случае последнее выражение преобразуется к виду:

Q = y2010 + K y2010 + K 2 y2010 + K 3 y2010 + K 4 y2010

Преобразуя левую часть и приводя подобные получим

4

∑ y201i K 4 + K 3 + K 2 + K = i=y12010

Таким образом, средняя величина темпа роста, удовлетворяющая поставленным условиям, будет находится из решения полученного линейного алгебраического уравнения четвертой степени.

Для случая произвольного изучаемого периода, состоящего из n уровней ряда, соответствующее уравнение запишется в виде

n

∑ yi

K n + K n−1 +...+ K 2 + K = i=y10

Средняя величина, найденная из данного соотношения, получила название средней параболической.

15

Вполне понятно, что решить данное уравнение аналитически для произвольного случая невозможно, поэтому используются приближенные методы решения.

Наибольшее распространение получила следующая форма средней параболической величины

риода; y0 – базисный уровень, то есть период, предшествующий изучаемому.

Отсюда средний темп прироста будет составлять

T = K −1.

Учитывая, что средних величин достаточно много и они не совпадают даже для одной и той же совокупности, естественно возникает вопрос об их соотношении. Это задается правилом мажорантности средних

xгармоническая ≤ xгеометрическая ≤

xарифметическая ≤ xквадратическая

При изучении структурных (позиционных средних) необходимо обратить внимание на тот факт, что для совокупности будет характерным три квартили и девять децилей. Причем вторая квартиль и пятая дециль будут совпадать с медианой данной совокупности.

Вопросы для самоконтроля

1.Докажите «нулевое» свойство средней арифметической величины.

2.Докажите «оптимальное» свойство средней арифметической величи-

ны.

3.В каких случаях применяется средняя геометрическая взвешенная?

4.В каких случаях применяется средняя гармоническая взвешенная?

5.В каких случаях применяется средняя гармоническая простая?

6.Каково значение средних величин в статистике?

7.Какие виды средних величин вы знаете?

8.В чем отличие простой средней арифметической от взвешенной? Чем обусловлено применение той или иной формы?

9.В каких случаях применяется средняя гармоническая?

10.Объясните понятие «исходное соотношение средней».

11.Перечислите основные свойства средней арифметической.

Тема №6 «Показатели вариации»

Вариация признака в совокупности. Значение ее изучения. Виды вариационных рядов и их графическое изображение. Показатели вариации и

16

способы их расчета. Виды дисперсии и правило их сложения. Проверка статистических гипотез.

Основное внимание необходимо уделить понятию вариации совокупности и способом ее количественного описания. Показать, что дисперсия имеет основной недостаток, который заключается в том, что единицы ее измерения будут являться квадратом единиц измерения элементов совокупности, например, исходные единицы совокупности измеряются в тоннах (т), тогда единица измерения дисперсии, вычисленной по этой совокупности будет т2 (тонна в квадрате). Естественно, в этом случае очень тяжело судить о степени разбросанности значений совокупности от средней величины. Именно поэтому и вводится новая величина, тесно связанная с дисперсией – среднее квадратическое отклонение (СКО) или стандартное отклонение.

Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются индивидуальные значения признака от своего среднего значения.

При изучении коэффициента вариации v следует обратить внимание на тот факт, что при изучении нескольких совокупностей имеющих различную природу, а, следовательно, и различные единицы измерения, невозможно сравнивать величину дисперсии, которая будет измеряться в разных величинах. Для таких сравнений необходимо использовать относительную величину. В качестве такой относительной величины и стали использовать коэффициент вариации.

В ходе изучения правила сложения (или разложения) дисперсии необходимо пояснить, что изучаемое правило сложения дисперсии справедливо только для случая, когда совокупность сгруппирована по одному единственному признаку. Если же это не так, то для этого случая используются более сложные методы многомерного статистического анализа, который в рамках данного курса не рассматривается.

Особо следует обратить внимание на возможность количественного определения тесноты связи между рассматриваемыми признаками на основе использования понятия межгупповой и общей дисперсий, путем вычисления эмпирического корреляционного отношения.

Вопросы для самоконтроля

1.В чем недостаток дисперсии

2.Для чего необходим коэффициент вариации

3.Что показывает средняя из внутригрупповых дисперсий

4.Что показывает межгрупповая дисперсия

5.Что такое вариация и каковы этапы ее статистического анализа?

6.Как определить моду и медиану в интервальном вариационном ряду?

7.Для чего рассчитываются относительные показатели вариации?

8.В чем состоит правило сложения дисперсий?

17

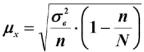
Тема №7 «Выборочное наблюдение»

Значение и теоретические основы выборочного наблюдения. Генеральная и выборочная совокупности. Их сводные характеристики. Методы и способы отбора единиц в выборочную совокупность. Ошибки выборки. Определение оптимальной численности выборки.

В основе выборочного метода лежит предположение о том, что на основании вычисленных характеристик выборочной совокупности можно сделать о значениях характеристик генеральной совокупности. Это предположение получило научное обоснование в виде теоремы Чебышева.

Особое внимание необходимо обратить на научно обоснованные способы формирования выборочной совокупности. В ходе отбора единиц выборочной совокупности необходимо обеспечить соблюдение следующих двух правил.

а) выборка из генеральной совокупности должна быть прове­дена случайно, то есть каждая ее единица должна иметь такую же вероятность попасть в выборку, как и остальные (так, например, отобранные наилучшие или наихудшие единицы не отображают действительное распределение признака в генеральной совокуп­ности);

б) выборка должна быть осуществлена из однородной совокупности, так как при других обстоятельствах результаты выборки будут не точными и не могут в полной мере представлять генеральную совокупность.

Нарушение этих принципов ведет к появлению систематической ошибки репрезентативности, что делает проведенное исследование ошибочным.

В ходе обсуждения задач, возникающих при выборочном наблюдении необходимо обратить внимание на определение предельной ошибки выборки. Она определяется согласно теореме Ляпунова

= t·μ

где μ – средняя квадратическая ошибка выборки или стандартная ошибка выборки.

Коэффициент доверия t при определении предельной ошибки зависит от принятого уровня вероятности Р: так, при t=1,0 значение вероятности

Р=0,683;

t=1,96 – для вероятности Р = 0,950; t=2,0 – для вероятности Р = 0,954; t=3,0 – для вероятности Р=0,997.

Формулы для вычисления средней квадратической ошибки выборки или стандартной ошибки зависят от способа организации выборочного обследования. Для простой случайной бесповторной выборки и механической выборки для средней величины стандартная ошибка будет определяться по формуле

для доли

18

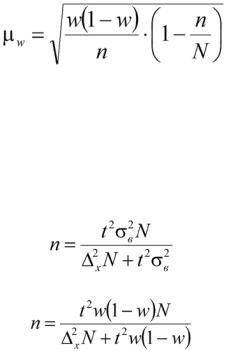
Для более сложных способов формирования выборочной совокупности стандартная ошибка такой выборки μ находится по формулам, известным из специальной литературы.

При решении задачи о нахождении необходимой численности выборки, которая с практической достоверностью обеспечивала бы заданную точность выборочных характеристик используются следующие формулы

а) для средней

б) для доли

В данном случае в этих выражениях все величины известны или могут быть определены из таблиц, но выборочная дисперсия и для средней величины, и для доли, как правило, остается неизвестной. Возникает вопрос о том, как ее определить. Это возможно сделать одним из следующих способов

–принять равной значениям из предыдущих выборочных наблюдений;

–по правилу, согласно которому в размахе вариации R=xmax – xmin укладывается примерно шесть стандартных отклонений. То есть в этом случае будет справедливо следующее соотношение

R/σ = 6 или R2/σ2= 36.

Тогда выборочная дисперсия будет определяться из соотношения

σ2= R2/36.

– по правилу «трех сигм», согласно которому в средней величине укладывается примерно три стандартных отклонения. В этом случае, используя выражение для коэффициента вариации, получим

Вопросы для самоконтроля

1.Какое наблюдение называют выборочным и где его используют? 2.Каковы преимущества выборочного наблюдения по сравнению с дру-

гими видами наблюдения?

3.Что означает репрезентативность выборки? При каких условиях выборка репрезентативна?

4.Что означают понятия генеральной и выборочной совокупности?

5.Какие подходы используются при создании случайной выборки?

6.Какие способы используются при формировании выборочной совокупности?

19

7.Какие разновидности выборки используются в экономической практике и их суть?

8.Виды выборки в статистических исследованиях.

9.Обобщающие характеристики генеральной и выборочной со вокупно-

стей.

10.Чем случайная ошибка репрезентативности отличается от систематической? Можно ли ее избежать?

11.Что позволяет установить теорема Чебышева закона больших чисел. 12.Что позволяет установить теорема Ляпунова закона больших чисел. 13.Как определяется предельная ошибка выборки?

14.Суть простой случайной выборки и ее применение в практике. 15.Какие задачи могут решаться при простой случайной выборке? 16.Преимущества бесповторной выборки перед повторной.

17.В чем заключается суть коэффициента доверия и как он определяется? 18.Структура формул для расчета средней ошибки и численности про-

стой случайной выборки в зависимости от средней и доли.

19.Суть механической выборки и ее практическое применение.

20.Разновидности механической выборки и их суть.

21.Суть районированной выборки и виды распределения между районами в выборочной совокупности.

22.Структура формул для расчета средней ошибки и численности районов в механической выборке в зависимости от средней и доли.

23.Суть типической выборки как разновидности районированной. 24.Суть серийной выборки и ее использование на практике. 25.Структура формул для определения средней ошибки и численности

выборки в сериях.

26.Суть ступенчатой выборки и ее практическое применения.

27.Структура формулы для определения средней ошибки в ступенчатой выборке.

28.Виды ступенчатой выборки.

29.Применение малой выборки для решения практических задач.

30.Особенности малой выборки в сравнении с большой.

31.Для каких случаев справедливы результаты, полученные Стьюдентом для малых выборок.

32.Что следует из теоремы Ляпунова?

Тема №8. «Статистические методы анализа корреляционных связей»

В ходе изучения различных социально-экономических явлений приходится сталкиваться с различными типами зависимостей. Как правило, различают функциональную и стохастическую зависимости.

Под функциональной понимается такая зависимость, когда одному значению независимого фактора обычно соответствует только одно значение

20