
- •Силы, действующие на движущиеся заряды и проводники с током в магнитном поле
- •Силы, действующие на движущиеся заряды и проводники с током в магнитном поле
- •394026 Воронеж, Московский просп., 14
- •Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2. Силы, действующие на движущиеся заряженные частицы в электростатическом и магнитном полях Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Сила, действующая на проводник с током в магнитном поле Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4. Работа по перемещению контура с током в магнитном поле Основные законы и формулы
- •П римеры решения задач
- •Задачи для самостоятельного решения
- •Библиографический список
- •Содержание
Задачи для самостоятельного решения
1.
Электрон в атоме водорода движется
вокруг ядра по круговой орбите некоторого
радиуса. Найти отношение магнитного
момента
 эквивалентного кругового тока к моменту
импульса
эквивалентного кругового тока к моменту
импульса
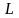 орбитального движения электрона. Заряд
электрона и его массу считать известными.
Указать направления векторов
орбитального движения электрона. Заряд
электрона и его массу считать известными.
Указать направления векторов
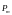 и
и
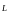 .
.
Ответ:
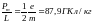
2.
По тонкому стержню, длиной
 равномерно распределён заряд Q=240нКл.
Стержень
приведён во вращение с постоянной
угловой скоростью
равномерно распределён заряд Q=240нКл.
Стержень
приведён во вращение с постоянной
угловой скоростью
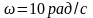 относительно оси, перпендикулярной
стержню и проходящей через его середину.
Определить: 1) магнитный момент
,
обусловленный вращением заряженного
стержня;
относительно оси, перпендикулярной
стержню и проходящей через его середину.
Определить: 1) магнитный момент
,
обусловленный вращением заряженного
стержня;
2) отношение магнитного момента к моменту импульса, если стержень имеет массу m=12г.
Ответ:

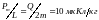
3.
Тонкое кольцо радиусом R=10см
несёт заряд Q=10нКл.
Кольцо
равномерно вращается с частотой
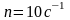 относительно оси, перпендикулярной
плоскости кольца и проходящей через
его центр. Найти: 1) магнитный момент
кругового тока, создаваемого кольцом;
2) отношение магнитного момента к моменту
импульса, если масса m
кольца равна
10г.
относительно оси, перпендикулярной
плоскости кольца и проходящей через
его центр. Найти: 1) магнитный момент
кругового тока, создаваемого кольцом;
2) отношение магнитного момента к моменту
импульса, если масса m
кольца равна
10г.
Ответ:
1)
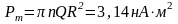
2)
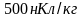
4. То же, что и в предыдущей задаче, но относительно оси, совпадающей с одним из диаметров кольца.
Ответ:
1)
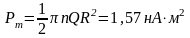 ;
2)
;
2)
5.
Диск радиусом R=10см
несёт равномерно распределённый по
поверхности заряд Q=0,2мкКл.
Диск равномерно вращается с частотой
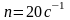 относительно оси, перпендикулярной
плоскости диска и проходящей через его
центр. Определить: 1) магнитный момент
кругового тока, создаваемого диском;
2) отношение магнитного момента к моменту
импульса, если масса m
диска равна
100г.
относительно оси, перпендикулярной
плоскости диска и проходящей через его
центр. Определить: 1) магнитный момент
кругового тока, создаваемого диском;
2) отношение магнитного момента к моменту
импульса, если масса m
диска равна
100г.
Ответ:
1)
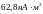 ,
2)
,
2)
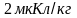
6.
Тонкостенная металлическая сфера
радиусом R=10см
имеет равномерно распределенный по её
поверхности заряд Q=3мКл.
Сфера равномерно вращается с угловой
скоростью
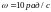 относительно оси, проходящей через
центр сферы. Найти: 1) магнитный момент
относительно оси, проходящей через
центр сферы. Найти: 1) магнитный момент
 кругового тока, создаваемый вращением
сферы; 2) отношение магнитного момента
к моменту импульса, если масса m сферы
равна 100г.
кругового тока, создаваемый вращением
сферы; 2) отношение магнитного момента
к моменту импульса, если масса m сферы
равна 100г.
Ответ:
1)

2)

2. Силы, действующие на движущиеся заряженные частицы в электростатическом и магнитном полях Основные законы и формулы
Сила
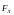 ,
действующая на заряд
,
действующая на заряд
 ,
движущийся со скоростью
,
движущийся со скоростью
 в электрическом поле напряженностью
в электрическом поле напряженностью
 и в магнитном поле с индукцией
и в магнитном поле с индукцией
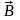 выражается формулой
выражается формулой
 .
.
Её называют силой Лоренца. Данное выражение справедливо как для постоянных, так и для переменных магнитных и электрических полей, причем, при любых значениях скорости заряда.
Примеры решения задач
1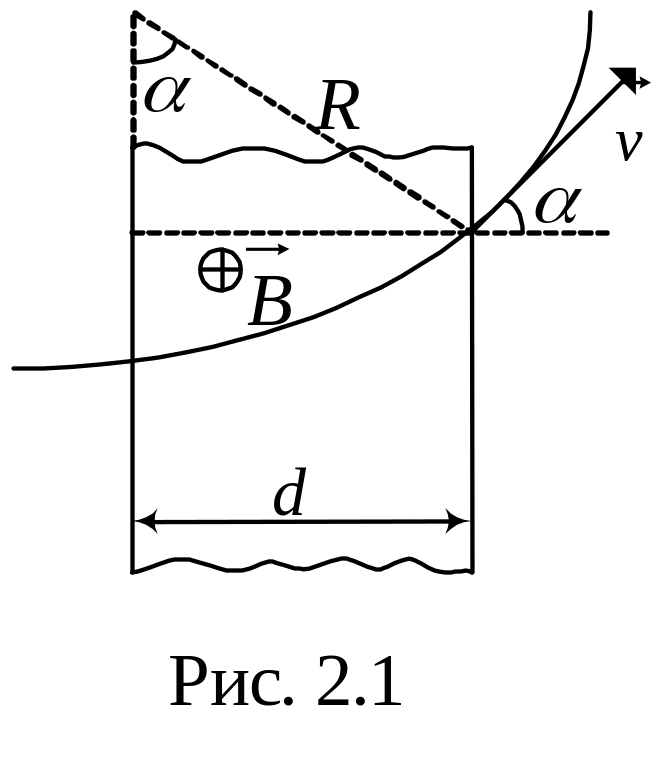 .
Протон, ускоренный разностью потенциалов
.
Протон, ускоренный разностью потенциалов
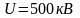 ,
пролетает поперечное однородное
магнитное поле, с индукцией
,
пролетает поперечное однородное
магнитное поле, с индукцией
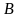 .
Толщина области с полем
.
Толщина области с полем
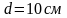 (рис.2.1).
Найти угол
(рис.2.1).
Найти угол
 отклонения протона от первоначального
направления движения.
отклонения протона от первоначального
направления движения.
Решение
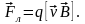 ,
т.к.
,
т.к.
 ,
,
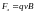 .
.
Вследствие того,
что
 протон движется по дуге окружности
радиуса R,
который
находится из условия, что результирующая
всех сил, действующих на частицу,
движущуюся равномерно по окружности,
является центростремительной силой.
протон движется по дуге окружности
радиуса R,
который
находится из условия, что результирующая
всех сил, действующих на частицу,
движущуюся равномерно по окружности,
является центростремительной силой.
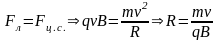 .
.
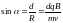 ( рис.2.1).
( рис.2.1).
Скорость протона находится из условия, что работа сил электростатического поля идет на увеличение кинетической энергии протона
![]() .
.
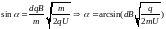 ,
,
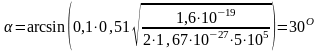 .
.
2.
Заряженная частица движется по окружности
радиуса
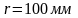 в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией
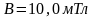 .
Найти её скорость и период обращения,
если частицей является:
.
Найти её скорость и период обращения,
если частицей является:
а) нерелятивистский протон;
б) релятивистский электрон.
Решение
а)
,
т.к.
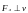 ,
траектория движения – окружность и
,
траектория движения – окружность и
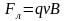 .
.
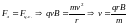 ,
,
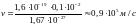 .
.
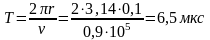 .
.
б)
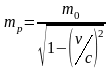 -
релятивистская масса частицы.
-
релятивистская масса частицы.
 ,
,
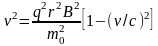 ,
,
 ,
,
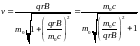 ,
,
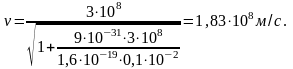
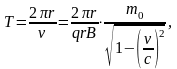
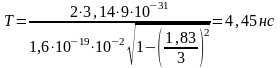 .
.
3.
Электрон, ускоренный разностью потенциалов
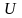 ,
пролетает поперечное магнитное поле с
индукцией
.
Толщина
области с полем
,
пролетает поперечное магнитное поле с
индукцией
.
Толщина
области с полем
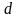 .
Определить траекторию движения электрона.
.
Определить траекторию движения электрона.
Решение
Радиус
траектории движения электрона
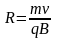 (см. реше-ние задачи 1).
(см. реше-ние задачи 1).
1)Если
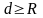 ,
электрон
описывает полуокружность и выходит из
области магнитного поля в противоположном
направлении.
,
электрон
описывает полуокружность и выходит из
области магнитного поля в противоположном
направлении.
2)Если
d
< R,
электрон выходит из области магнитного
поля под углом
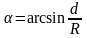 к горизонту.
к горизонту.
3) Если
 ,
то
,
то
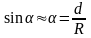 .
.
4. Протон с энергией 10МэВ попадает в магнитное поле с индукцией 1Тл под углом 60° к вектору магнитной индукции. Определить радиус, период и шаг винтовой траектории протона. (1эВ = 1,6• 10-19 Дж) .
Решение
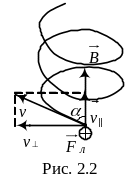
,
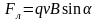 ,
,
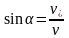 (рис.2.2).
(рис.2.2).
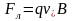 .
.
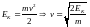 .
.
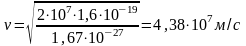 .
.
 .
.
 ,
,
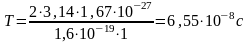 .
.
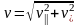 ,
,
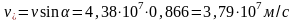 ,
,
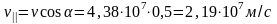 .
.
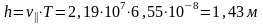 .
.
5.
Альфа-частица прошла ускоряющую разность
потенциалов
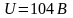 и влетела в скрещенные под прямым углом
электрическое (
и влетела в скрещенные под прямым углом
электрическое ( )
и магнитное (
)
и магнитное ( )
поля. Найти отношение заряда альфа -
частицы к её массе, если двигаясь
перпендикулярно обоим полям частица
не испытывает отклонений от прямолинейной
траектории (рис.2.3).
)
поля. Найти отношение заряда альфа -
частицы к её массе, если двигаясь
перпендикулярно обоим полям частица
не испытывает отклонений от прямолинейной
траектории (рис.2.3).
Р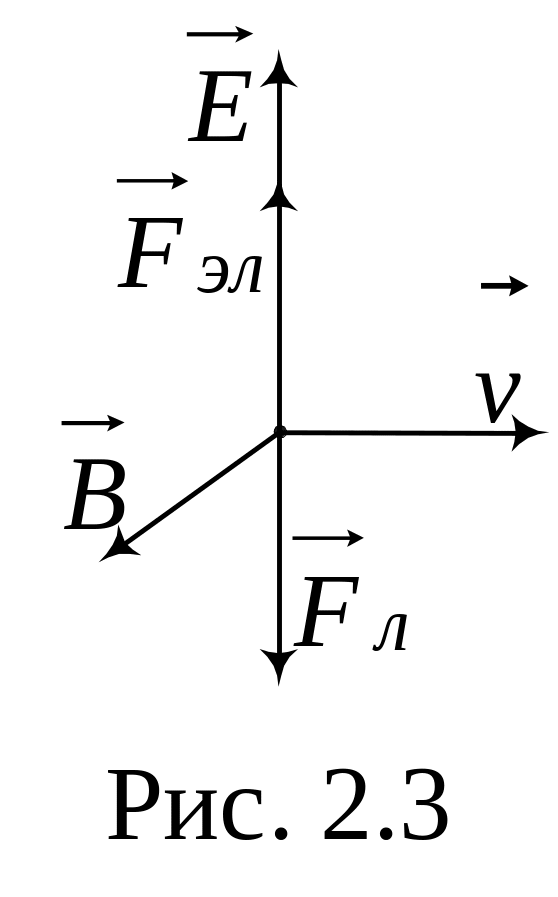 ешение
ешение
Работа сил электростатического поля идет на увеличение кинетической энергии частицы. Полагая начальную энергию частицы равной нулю, запишем
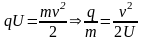 .
.
Альфа –
частица
является классической частицей, т.к. её
энергия много меньше энергии покоя
электрона
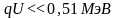 .
.
Так как частица
движется равномерно и прямолинейно, то
сила
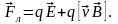 ,
действующая на частицу равна нулю и
,
действующая на частицу равна нулю и
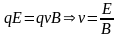 .
.
 .
.
6.
Прямолинейный проводник длиной
 вращается равномерно с угловой скоростью
вокруг
вертикальной оси, проходящей через его
конец в магнитном поле с индукцией
,
направленной
перпендикулярно плоскости вращения
проводника. Направление векторов
вращается равномерно с угловой скоростью
вокруг
вертикальной оси, проходящей через его
конец в магнитном поле с индукцией
,
направленной
перпендикулярно плоскости вращения
проводника. Направление векторов
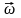 и
совпадают.
Определить разность потенциалов на
концах проводника.
и
совпадают.
Определить разность потенциалов на
концах проводника.
Решение
.
 .
.
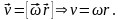
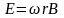 .
.
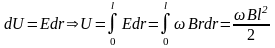 .
.
