3.1.4 Переменные в Matlab. Массивы и матрицы
В любой области MATLAB можно определить переменные, а затем использовать в выражениях.
Любая переменная до использования в формулах и выражениях должна быть определена. Для определения переменной необходимо набрать ее имя, символ «=» и значение переменной. Здесь знак равенства – это оператор присваивания, действие которого не отличается от других языков программирования.
Имя переменной не должно совпадать с именами встроенных процедур, функций и встроенных переменных системы может содержать до 19 символов. Система различает большие и малые буквы в именах переменных. То есть ABC, abc, Abc, aBc – это имена разных переменных.
Выражение в правой части оператора присваивания может быть числом, арифметическим выражением, строкой символов или символьным выражением. Отметим, что если речь идет о символьной или строковой переменной, то выражение в правой части оператора присваивания следует брать в одинарные кавычки.
Несколько примеров присвоения значений переменным приведено в листинге 1. Обратите внимание, что если символ «;» в конце выражения отсутствует, то в качестве результата выводится имя переменной и ее значение. Наличие символа «; » передает управление следующей командной строке. Это позволяет использовать имена переменных для записи промежуточных результатов в память компьютера.
Листинг 1.
>> а=2.3
а =
2.3000
» b=-34.7
b =
-34.7000
» х-1;у=2;
» z=(х+у)-а/Ь
z =
3.0663
>>%------------------------------------------------
>>%Сообщение об ошибке - переменная с не определена
» с+3/2
??? Undefined function or variable 'с'.
>>%------------------------------------------------
»%Определение символьной переменной
» с='а'
c=
а
»%Определение строковой переменной
» h='мама мыла раму'
h =
мама мыла раму
Вы обратили внимание, что если команда не содержит знака присваивания, то по умолчанию вычисленное значение присваивается специальной системной переметром ans. Причем полученное значение можно использовать в последующих вычислениях, но важно помнить, что значение ans изменяется после каждого вызова команды без оператора присваивания.
Кроме переменной ans в MATLAB существуют и другие системные переменные:
ans - результат последней операции без знака присваивания;
i, j - мнимая единица (
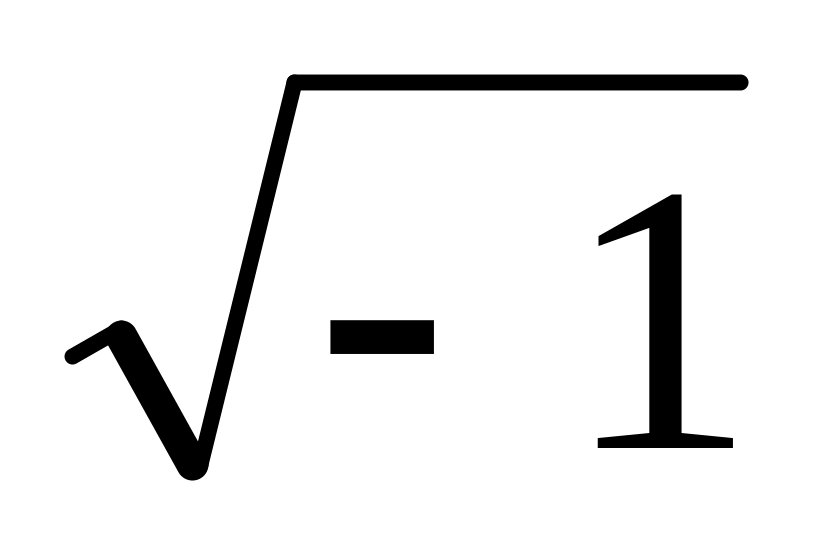);pi - число п (3.141592653589793);
inf - машинный символ бесконечности (∞);
NaN - неопределенный результат (0/0, ∞/∞, 1∞ и т.п.);
realmin - наименьшее число с плавающей точкой (2.2251е - 308);
realmax - наибольшее число с плавающей точкой (1.7977е + 308).
Для работы со множеством данных оказывается удобным использовать массивы.
Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив - множественный тип данных, состоящий из фиксированного числа элементов. Как и любой другой переменной, массиву должно быть присвоено имя.
Переменную, представляющую собой просто список данных, называют одномерным массивом или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом.
Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй номеру столбца, в которых хранится необходимый элемент.
Значение нижней границы индексации в МАТLАВ равно единице. Индексы могут быть только целыми положительными числами или нулем.
Самый простой способ задать одномерный массив в МАТLАВ имеет вид:
[nаmе]=
где
nаmе
- имя переменной, в которую будет записан
сформированный массив, ХN
- значение первого элемента массива, Хk
- значение последнего его элемента, dx-
шаг, с помощью которого формируется
следующий элемент массива, то есть
значение второго элемента составит
Xn+dx,
третьего Xn+dx+dx
и так далее до Xk.
Если параметр dx
в конструкции отсутствует: [nаmе]=
это означает,
что по умолчанию он принимает значение,
равное единице, то есть каждый следующий
элемент массива равен значению предыдущего
плюс один.
Примеры создания массивов приведены в листинге 3. Обратите внимание, что переменную, заданную как массив, можно использовать в арифметических выражениях и в качестве аргумента математических функций. Результатом работы таких операторов являются массивы.
Листинг 2.
>>Xn=-3.5;dX=1.5;Xk=4.5;
>> X=Xn:dx:Xk
X=-3.5000 -2.0000 -0.5000 1.0000 2.5000 4.0000
>> Y=sin(X/2)
Y= -0.9840 -0.8415 -0.2474 0.4794 0.9490 0.9093
>> A=0:5
A=
0 1 2 3 4 5
ans=
0 1 2 3 4 5
>> ans/2+pi
ans=
3.1416 3.6416 4.1416 4.6416 5.1416 5.6416
Еще один способ задания векторов и матриц в МАТLАВ - это их поэлементный ввод. Так, для определения вектор-строки следует ввести имя массива, а затем, после знака присваивания, в квадратных скобках через пробел или запятую перечислить элементы массива (листинг 4).
Листинг 3.
>> V=[1 2 3 4 5]
V=
1 2 3 4 5
>> W=[1.1,2.3,-0.1,5.88]
W=
1.1000 2.3000 -0.1000 5.8800
Элементы вектора-столбца вводятся через точку с запятой.
Листинг 4.
>> X=[1;2;3]
X=
1
2
3
Обратиться к элементу вектора можно, указав имя массива и порядковый номер элемента в круглых скобках.
Листинг 5.
>> W=[1.1,2.3,-0.1,5.88]
>> W=W(1)+2*(3)
ans=
0.9000
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом все элементы строки отделяются друг от друга запятой или пробелом, а строки разделяются точкой с запятой. Обратиться к элементу матрицы можно, указав после имени матрицы в круглых скобках через запятую номера строки и столбца, на пересечении которых расположен элемент. Примеры задания матриц и обращения к их элементам показаны в листинге 6.
Листинг 6.
>>% Ввод матрицы по строкам
>> М=[1 2 3;4 5 6]
М=
1 2 3
4 5 6
>>% Обращение к элементу матрицы
>> М (2,2)
ans=
5
>>% Замена элемента матрицы
>> М (1,3)=pi;
>> М
M=
1.0000 2.0000 3.1416
4.0000 5.0000 6.0000