§4. Уравнение центральной винтовой оси

П

Рис. 59.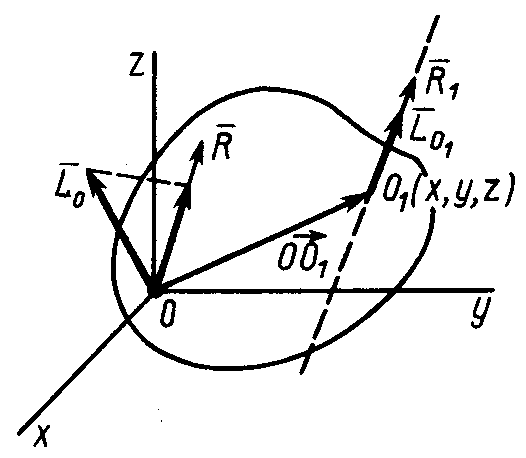

редположим, что в центре приведения, принятом за начало координат, получены главный вектор с проекциями на оси координат и главный момент с проекциями . При приведении системы сил к центру приведения (рис. 59) получается динама с главным вектором и главным моментом . Векторы , и , как образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем . Имеем

, (71)

так как . Главные моменты и , согласно (64), удовлетворяют соотношению

. (64)

Подставляя из (64) в (71), получим

. (71’)

Координаты точки в которой получена динама, обозначим . Тогда проекции вектора на оси координат равны координатам . Учитывая это, (71’) можно выразить в форме

, (71”)

где – единичные векторы осей координат; а векторное произведение представлено определителем. Векторное уравнение (71”) эквивалентно трем скалярным, которые после отбрасывания можно представить в виде:

. (72)

Линейные уравнения (72) для координат являются уравнениями прямой линии – центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.

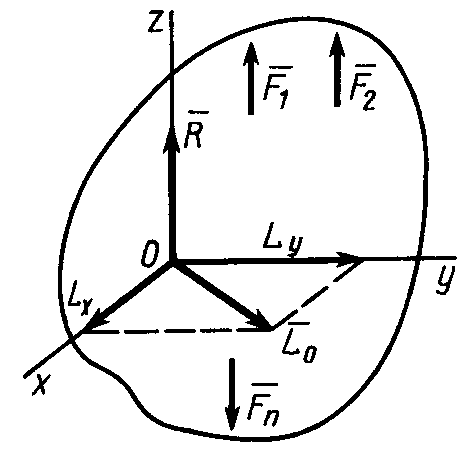
§5. Частные случаи приведения пространственной системы параллельных сил

В отличие от произвольной системы сил пространственная система параллельных сил не приводится к динаме, так как для нее главный вектор и главный момент в общем случае взаимно перпендикулярны. Для доказательства этого рассмотрим пространственную систему параллельных сил, для которой главный вектор и главный момент не равны нулю. Выберем за центр приведения точку О – начало декартовой системы координат, ось которой направим параллельно силам (рис. 60). Тогда проекции главного вектора на оси координат

,

,

т

Рис. 60

ак как параллельные силы перпендикулярны этим осям. Только проекция главного вектора на ось в общем случае не равна нулю. Она равна алгебраической сумме параллельных сил, т. е.

.

Следовательно, главный вектор параллелен оси .

Для проекций главного момента на оси координат имеем:

, , .

Проекция главного момента на ось равна нулю, так как каждая сила параллельна этой оси.

Таким образом, главный момент расположен в плоскости , перпендикулярной главному вектору, направленному по оси . В этом случае система сил приводится к равнодействующей.

Для системы параллельных сил возможны следующие частные случаи приведения:

и – система приводится к паре сил;

и или и – система приводится к равнодействующей силе;

и – имеем равновесную систему сил.

Если главный вектор не равен нулю, то система параллельных сил приводится только к равнодействующей силе, параллельной главному вектору и равной ему по величине.

§6. Центр системы параллельных сил

Для систем параллельных сил, приводящихся к равнодействующей, введем понятие центра параллельных сил. Для этого предположим, что на твердое тело действует система параллельных сил , приводящаяся к равнодействующей, силы которой приложены в точках . При введении понятия центра параллельных сил считаем силы приложенными в точках твердого тела. При переносе сил вдоль линий действия положение центра параллельных сил изменяется.

О

Рис. 61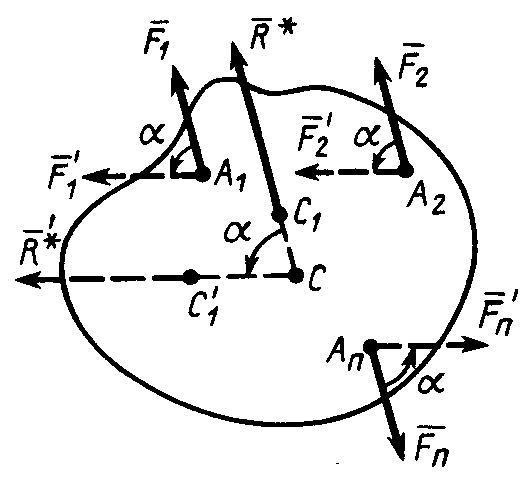

пределим линию действия равнодействующей параллельных сил для заданного направления этих сил. Затем через точки приложения параллельных сил проведем взаимно параллельные оси, перпендикулярные силам. Повернем параллельные силы вокруг этих осей на общий угол в одном и том же направлении (рис. 61). Получим новую систему параллельных сил . Равнодействующая этой системы параллельных сил равна по модулю равнодействующей силе , так как при повороте числовые значения параллельных сил не изменялись.

Линии действия двух равнодействующих сил и пересекутся в точке С, которая и называется центром параллельных сил. Если равнодействующую силу приложить в точке С вместо , то при повороте заданных параллельных сил на угол она повернется на тот же угол а вокруг оси, проходящей через точку С и параллельной осям, вокруг которых поворачиваются заданные параллельные силы. Оси поворота параллельных сил должны быть перпендикулярны параллельным силам.

Центр параллельных сил не зависит от угла поворота и направления параллельных осей, вокруг которых поворачиваются параллельные силы. Из определения центра параллельных сил следует, что его положение зависит от точек приложения параллельных сил. Поэтому параллельные силы следует считать приложенными в точках твердого тела.

Получим формулу для определения радиуса-вектора центра параллельных сил, если известны параллельные силы и радиусы-векторы точек их приложения. Для этого выберем единичный вектор , параллельный силам. Тогда каждая из параллельных сил

где – алгебраическое значение силы. Оно положительно, если сила направлена в одну сторону с единичным вектором , и отрицательно, если направление силы противоположно направлению единичного вектора.

Для равнодействующей силы параллельных сил соответственно имеем

.

Так как система параллельных сил, по предположению, приводится к равнодействующей, то к ней можно применить теорему Вариньона относительно точки О:

. (73)

Для векторных моментов сил относительно точки О имеем :

,

,

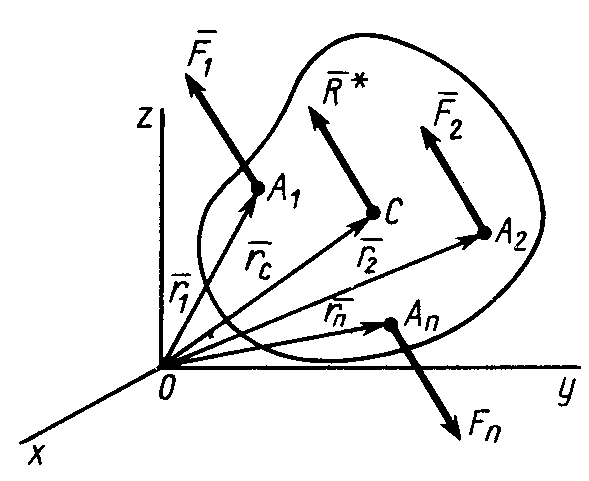где – радиус-вектор центра параллельных сил, проведенный из точки О; – радиус-вектор точки приложения силы проведенный из той же точки (рис. 62).

Е

Рис. 62

сли подставить эти значения векторных моментов сил в (73), то после переноса всех слагаемых в левую часть равенства и вынесения за скобку общего множителя получим

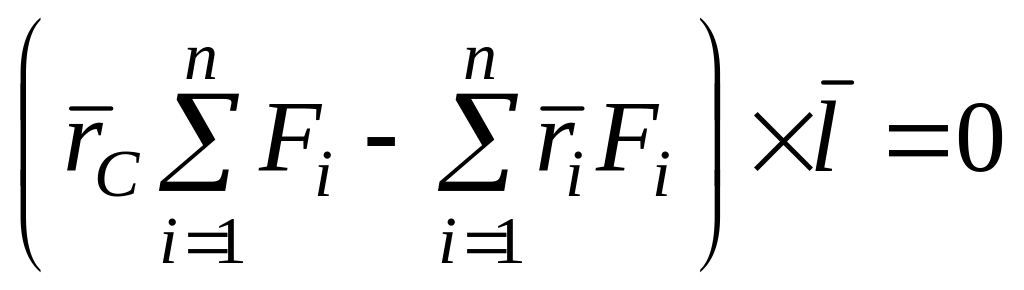. (73’)

Так как центр параллельных сил, а следовательно, и его радиус-вектор не зависят от направления параллельных сил, характеризуемого единичным вектором , то условие (73’) должно выполняться при любом направлении этого вектора.

Это возможно только при обращении в нуль векторной величины, стоящей в скобках, т. е.

,

или 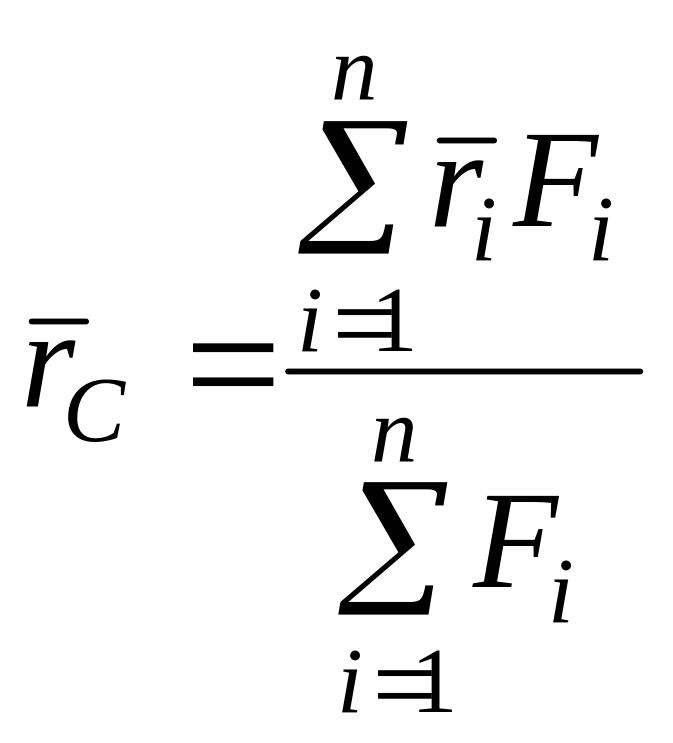. (74)

По формуле (74) определяют радиус-вектор центра параллельных сил, если заданы эти силы и их точки приложения.

Так как алгебраические значения параллельных сил входят в числитель и в знаменатель (74), то не зависит от того, какое из двух направлений параллельных сил считается положительным.

В проекциях на оси координат из (74) получаем:

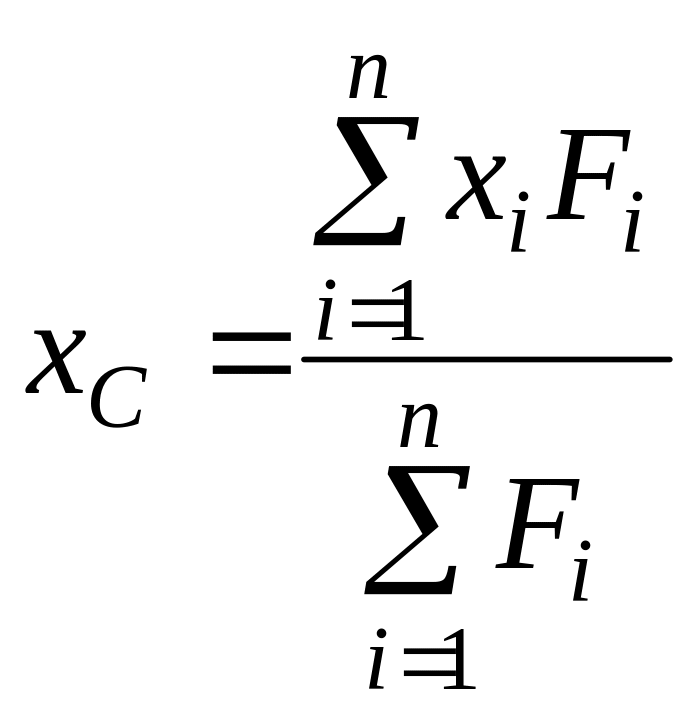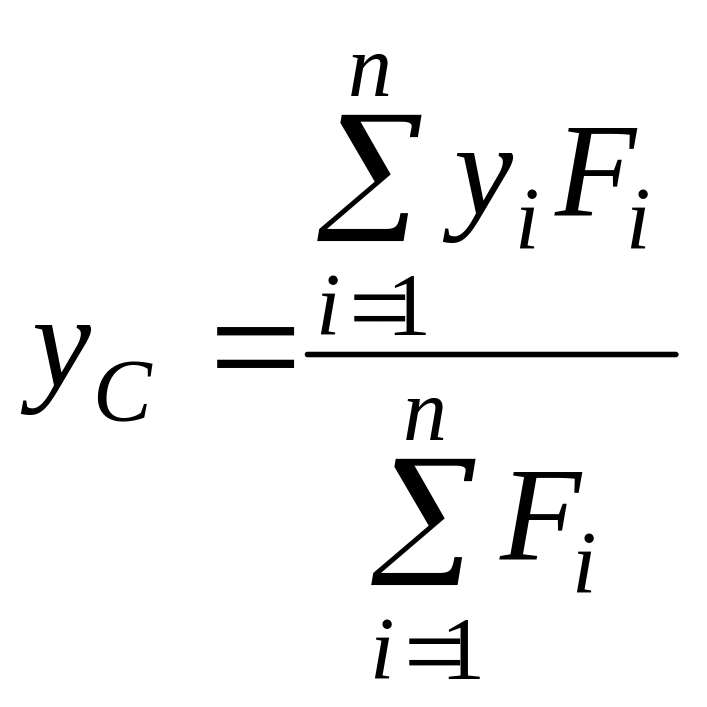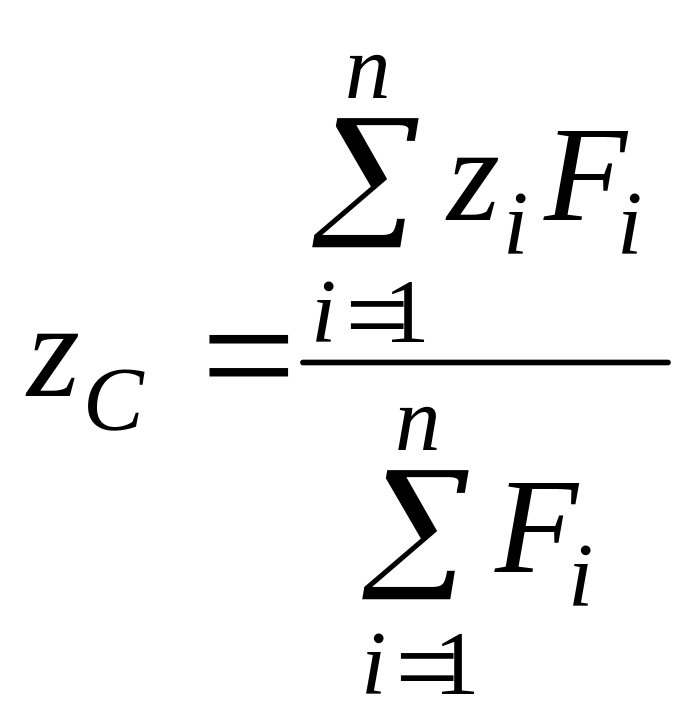, , . (75)

По формулам (13) вычисляют координаты центра параллельных сил , если известны алгебраические значения параллельных сил и координаты точек приложения этих сил .

Векторную величину

называют статическим моментом системы параллельных сил относительно точки О. Алгебраические величины

, ,

называют статическими моментами относительно координатных плоскостей. Для плоской системы параллельных сил, расположенных, например, в плоскости Оху, вводят понятие статических моментов относительно осей координат Ох и Оу по формулам:

, .

Статические моменты параллельных сил относительно точки и координатных плоскостей определяются по единому правилу: алгебраические значения сил умножают на расстояния от точек приложения сил до точки или плоскости и результаты суммируют. Расстояния от точек приложения сил до координатных плоскостей есть величины скалярные; это соответствующие координаты этих точек. Расстояния от точки О до точек приложения параллельных сил берутся векторные. Ими являются радиусы-векторы точек приложения параллельных сил, проведенные из точки О.