
- •Часть 1
- •Введение
- •I. Основные понятия и аксиомы. Сходящиеся силы
- •§ 1. Основные понятия и определения
- •§ 2. Аксиомы статики
- •§ 3. Простейшие теоремы статики
- •§ 4. Система сходящихся сил
- •П риведение к равнодействующей силе
- •Условия равновесия системы сходящихся сил
- •Проецирование силы на оси координат
- •II. Моменты силы относительно точки и оси
- •§ 1. Алгебраический момент силы относительно точки
- •§ 2. Векторный момент силы относительно точки
- •§ 3. Момент силы относительно оси
- •§ 4. Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
- •§ 5. Формулы для моментов силы относительно осей координат
- •III. Теория пар сил
- •§ 1. Пара сил и алгебраический момент пары сил
- •§ 2. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости
- •§ 3. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости
- •§ 4. Векторный момент пары сил
- •§ 5. Эквивалентность пар сил
- •§ 6. Теорема о сумме моментов сил пары
- •§ 7. Сложение пар сил
- •§ 8. Равновесие пар сил
- •IV. Приведение системы сил к простейшей системе. Условия равновесия
- •§ 1. Приведение произвольной системы сил к силе и паре сил
- •Приведение силы к заданному центру
- •П риведение произвольной системы сил к силе и паре сил
- •Приведение плоской системы сил
- •Формулы для вычисления главного вектора и главного момента
- •§ 2. Условия равновесия системы сил Условия равновесия системы сил в векторной форме
- •Условия равновесия пространственной системы сил в аналитической форме
- •Условия равновесия пространственной системы параллельных сил
- •Условия равновесия плоской системы сил
- •V. Плоская система сил. Теорема вариньона
- •§ 1. Частные случаи приведения плоской системы сил
- •Случай приведения к равнодействующей силе
- •Случай приведения к паре сил
- •§ 2. Теорема о моменте равнодействующей силы (Теорема Вариньона)
- •§ 3. Различные формы условий равновесия плоской системы сил
- •Теорема о трех моментах (вторая форма условий равновесия)
- •Третья форма условий равновесия
- •§ 4. Статически определимые и статически неопределимые задачи
- •§ 5. Равновесие системы тел
- •§ 6. Распределенные силы
- •Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии
- •Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону
- •Реакция заделки
- •§7. Решение задач на равновесие плоской системы сил, приложенных к твердому телу и системе тел
- •VI. Трение
- •§ 1. Трение скольжения
- •Законы Кулона
- •Угол и конус трения
- •Равновесие тела на шероховатой поверхности
- •§2. Трение качения
- •VII. Частные случаи пространственных систем сил. Центр параллельных сил
- •§ 1. Изменение главного момента при перемене центра приведения
- •§ 2. Инварианты системы сил
- •§ 3. Частные случаи приведения пространственной системы сил
- •§4. Уравнение центральной винтовой оси
- •§5. Частные случаи приведения пространственной системы параллельных сил
- •§6. Центр системы параллельных сил
- •§7. Частные случаи равновесия твердого тела Равновесие твердого тела с двумя закрепленными точками
- •Твердое тело с одной закрепленной точкой
- •Библиографический список
- •Оглавление
- •II. Моменты силы относительно точки и оси………………... 24
- •III. Теория пар сил……………………………………………... 32
- •IV. Приведение системы сил к простейшей системе. Условия равновесия…………………………………………… 44
- •V. Плоская система сил. Теорема Вариньона………………... 55
- •VI. Трение………………………………………………………. 73
- •VII. Частные случаи пространственных систем сил. Центр параллельных сил………………………………………. 86
- •Библиографический список………………………………….. 104
- •Часть 1
- •394026 Воронеж, Московский просп., 14
VII. Частные случаи пространственных систем сил. Центр параллельных сил
§ 1. Изменение главного момента при перемене центра приведения
П
Рис. 52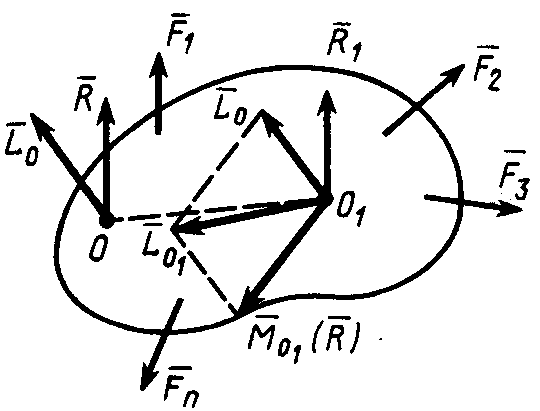
![]() (рис. 52). Выберем в качестве центра
приведения другую точку
(рис. 52). Выберем в качестве центра
приведения другую точку
![]() и вычислим главный момент
и вычислим главный момент
![]() рассматриваемой системы сил. Так как
рассматриваемой системы сил. Так как
~![]() ,
то для получения главного момента
достаточно привести к новому центру
систему
,
то для получения главного момента
достаточно привести к новому центру
систему
![]() .
Силу
из точки О перенесем в точку
.
Получим в этой точке силу
.
Силу
из точки О перенесем в точку
.
Получим в этой точке силу
![]() и, согласно теореме о параллельном
переносе силы, присоединенную пару сил
с векторным моментом
и, согласно теореме о параллельном
переносе силы, присоединенную пару сил
с векторным моментом
![]() .
Векторный момент пары сил
,
вычисленный относительно точки О как
вектор свободный, можно приложить в
любой точке тела. Новый главный момент
относительно точки
по правилу сложения пар сил является
векторной суммой моментов
и
,
т. е.
.
Векторный момент пары сил
,
вычисленный относительно точки О как
вектор свободный, можно приложить в
любой точке тела. Новый главный момент
относительно точки
по правилу сложения пар сил является
векторной суммой моментов
и
,
т. е.
![]() ;
;
![]() . (63)
. (63)
По формуле для векторного момента силы имеем
![]() .
.
С учетом этого формула (63) примет вид
![]() . (64)
. (64)
Итак, главный момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора , приложенного в старом центре приведения, относительно нового центра приведения .
§ 2. Инварианты системы сил
Инвариантами в
статике называются такие величины для
рассматриваемой системы сил, которые
не изменяются при изменении центра
приведения. Одним
из инвариантов является главный вектор,
так как в любом центре приведения он
выражается векторной суммой системы
сил. Если в одном центре приведения
![]() главный вектор
,
а в другом
,
он
главный вектор
,
а в другом
,
он
![]() ,
то
,
то
![]() . (65)
. (65)
Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
Из векторного равенства (65) следует, что равны модули и проекции главных векторов на любые оси координат, т. е.
![]() ,
,
![]() ,
,
![]() ,
,
![]() . (65’)
. (65’)
Для получения второго, скалярного, инварианта используем формулу (64):
.
Умножая обе части этого равенства скалярно на , причем в правой части при умножении вместо , согласно (65), возьмем , получим
![]() ,
,
или
![]() , (66)
, (66)
так как смешанное произведение векторов, содержащих два одинаковых множителя , равно нулю, т. е.
![]() .
.
Соотношение (66)
является вторым скалярным инвариантом:
скалярное
произведение главного момента на главный
вектор не зависит от центра приведения.
Второй скалярный инвариант можно
выразить в двух других эквивалентных
формах, если раскрыть скалярное
произведение векторов в (66). Обозначая
проекции
на оси координат через
![]() ,
,
![]() ,
,
![]() ,
а проекции
– соответственно
через
,
а проекции
– соответственно
через
![]() ,
,
![]() ,
,
![]() ,
второй инвариант можно выразить в форме
,
второй инвариант можно выразить в форме
![]() . (66’)
. (66’)
К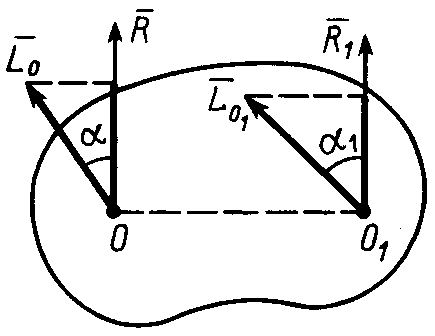 роме
того, формуле (66) можно придать вид:
роме
того, формуле (66) можно придать вид:
![]() ,
,
г
Рис. 53![]() – угол между векторами
и
– угол между векторами
и
![]() ,
а
– между
и
(рис.53). После сокращения на
,
а
– между
и
(рис.53). После сокращения на
![]() получим
получим
![]() .
(66”)
.
(66”)
В этой форме второй инвариант утверждает, что проекция главного момента на направление главного вектора не зависит от центра приведения.
Если главный момент в каждом центре приведения разложить на две взаимно перпендикулярные составляющие, одна из которых направлена по главному вектору, то, учитывая, что главные векторы в различных центрах приведения параллельны, согласно (66”), получим
![]() , (67)
, (67)
где
![]() – составляющая главного момента
по направлению главного вектора
,
а
– составляющая главного момента
по направлению главного вектора
,
а
![]() —составляющая
главного момента
по направлению главного вектора
.
Соотношение (67) является следствием
первого и второго инвариантов.
—составляющая
главного момента
по направлению главного вектора
.
Соотношение (67) является следствием
первого и второго инвариантов.
Рассмотренные инварианты (65) и (66) являются независимыми, т.е. из одного не следует другой. Комбинируя эти инварианты, можно получить другие, зависящие от них инварианты.
