§ 2. Теорема о моменте равнодействующей силы (Теорема Вариньона)
Д
Рис. 35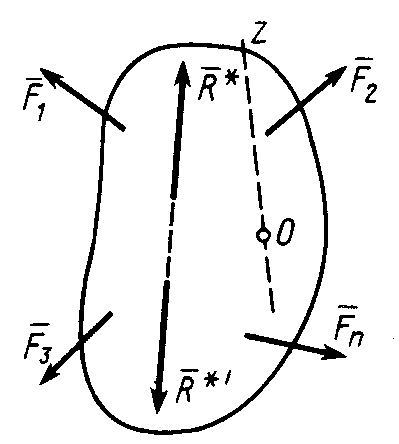
Пусть на твердое тело действует любая система сил (рис. 35), имеющая равнодействующую , т. е.
~ . (46)
Добавим
к заданной системе сил ее уравновешивающую
силу
,
которая равна по модулю, но противоположна
по направлению равнодействующей силе
и имеет с ней общую линию действия. Тогда
~
,
(47)
т.е. при добавлении к системе сил уравновешивающей силы, согласно определению уравновешивающей силы, образуется новая система сил, эквивалентная нулю и, следовательно, удовлетворяющая условиям равновесия системы сил, приложенных к твердому телу. В частности, сумма векторных моментов сил этой новой системы сил относительно любой точки О равна нулю:
,
но
,
так как и – две равные и противоположно направленные силы, действующие вдоль одной прямой. Получаем:
.
Отсюда следует теорема Вариньона:
. (48)
Если правую и левую части векторного равенства (48) спроецировать на произвольную ось Оz, проходящую через точку О, то, учитывая связь момента силы относительно оси с проекцией векторного момента относительно точки на оси, получим теорему Вариньона относительно оси Оz:
, (49)
т.е. момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
Для случая плоской системы сил, если точку О выбрать в плоскости действия сил, из (48) получаем:
. (50)
Это теорема Вариньона для плоской системы сил: алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.
§ 3. Различные формы условий равновесия плоской системы сил
В § 2 гл. IV получены общие условия равновесия плоской системы сил, действующих на твердое тело, в следующей форме:
.
(51)
Условия равновесия (51) назовем условиями равновесия плоской системы сил в первой форме.
Условия равновесия плоской системы сил, приложенных к твердому телу, можно сформулировать в других эквивалентных формах. Существуют еще две эквивалентные формы необходимых и достаточных условий равновесия.
Рассмотрим эти условия равновесия в виде теоремы о трех моментах и третьей формы условий равновесия.
Теорема о трех моментах (вторая форма условий равновесия)
Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю, т.е.
. (52)
Н
Рис. 36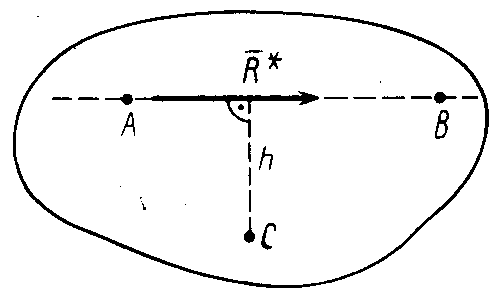
еобходимость
этих условий равновесия плоской системы
сил обусловлена тем, что если плоская
система сил находится в равновесии, то
силы этой системы удовлетворяют условиям
равновесия в первой основной форме
(51). А тогда из последнего условия (51)
следует, что сумма алгебраических
моментов сил относительно любой точки
(следовательно, и точек А, В, С) равна
нулю (рис. 36).
Для доказательства достаточности условий (52) для равновесия плоской системы сил, действующих на твердое тело, можно привести следующие рассуждения. Так как главные моменты относительно трех точек А, В и С равны нулю, то для любой из этих точек, взятых за центр приведения, система приводится или к равнодействующей, если главный вектор системы отличен от нуля, или система сил оказывается в равновесии, если главный вектор системы равен нулю. Предположим, что она приводится к равнодействующей силе . Тогда если выбрать за центр приведения точку А, то, используя теорему Вариньона (50), согласно (52), получим
.
Выбрав за центр приведения точку В, аналогично имеем
.
Эти условия для равнодействующей силы , отличной от нуля, могут выполняться в том случае, если линия действия равнодействующей силы проходит через точки А и В.
Из последнего условия (52) после применения теоремы Вариньона получаем
.
Но
,
так как точка С не находится на прямой,
проходящей через точки А и В. Следовательно,
равнодействующая сила равна нулю, что
и является достаточным условием
равновесия плоской системы сил,
приложенных к твердому телу.