§ 2. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости

Докажем, что пары сил, расположенные в одной плоскости, по своему действию на тело отличаются одна от другой только алгебраическими моментами.

Д

Рис. 23

ве пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Д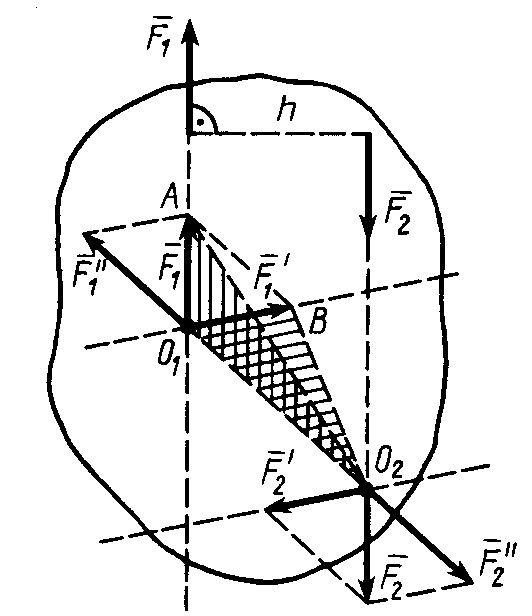 окажем теперь следующую теорему об эквивалентности двух пар сил: пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент. Иначе: две пары сил, расположенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты.

Пусть на твердое тело действует пара сил с алгебраическим моментом (рис. 23). Перенесем силу в точку О₁, а силу – в точку О₂, проведем через точки О₁ и О₂ две любые параллельные прямые, пересекающие линии действия сил пары и лежащие, следовательно, в плоскости действия заданной пары сил. Соединив прямой точки О₁ и О₂, разложим силы в точке О₁ и – в точке О₂ по правилу параллелограмма, как указано на рис. 23. Тогда

,

.

Так как силы и образуют пару сил, то

и, следовательно,

,

.

Итак

~ ~ ,

т.к. ~0 и, следовательно, эту систему двух сил можно отбросить.

Таким образом, заданную пару сил заменим другой парой сил . Докажем, что алгебраические моменты у этих пар сил одинаковы. Направление вращения у них одно и то же. Имеем:

;

.

Но , так как эти треугольники имеют общее основание О₁О₂ и равные высоты (их вершины расположены на общей прямой, параллельной основанию).

Таким образом, теорема доказана и можно сделать следующие выводы:

а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;

б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Эти операции над парами сил не изменяют их действия на твердое тело.

§ 3. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости

Д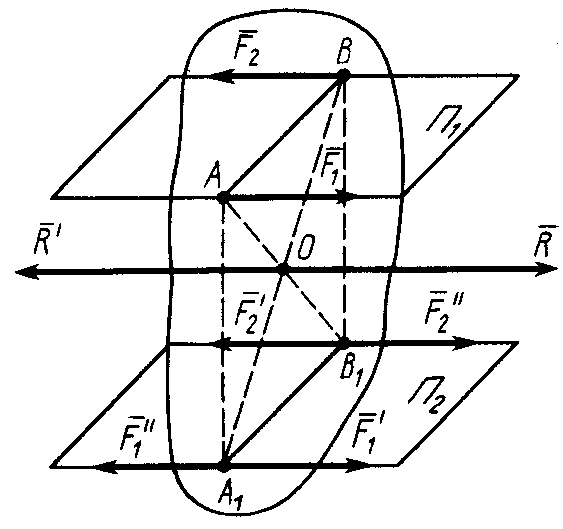 ействие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость (рис. 24).

Д

Рис. 24

ля доказательства этой теоремы к паре сил в точках А₁ и В₁, где перпендикуляры, опущенные из точек А и В плоскости , пересекаются параллельной ей плоскостью , приложим две системы сил и , каждая из которых эквивалентна нулю, т. е.

, .

Выберем силы и так, чтобы они удовлетворяли условиям

и

Сложим две равные и параллельные силы и . Их равнодействующая параллельна этим силам, равна их сумме и приложена посередине отрезка АВ₁ в точке О, так как складываются равные параллельные силы. Равнодействующая двух равных параллельных сил и тоже равна их сумме, параллельна им и приложена на середине отрезка ВА₁, т.е. в точке О, где пересекаются диагонали прямоугольника АВА₁В₁. Так как , то система сил эквивалентна нулю и ее можно отбросить.

Таким образом, пара сил эквивалентна такой же паре сил , но лежащей в другой, параллельной плоскости. Пару сил, не изменяя ее действия на твердое тело, можно перенести из одной плоскости в другую, параллельную ей.