6. Основные положения метода конечных элементов

6.1. Роль вычислительных методов в расчетах на прочность. Основные этапы численного исследования прочности конструкций.

Экстремальные условия работы элементов современных конструкций, сложность их формы и большие габариты делают исключительно трудным и дорогим осуществление натурного или полунатурного эксперимента, особенно, если речь идет об установлении предельных (разрушающих) нагрузок. Создание конструкций такого типа невозможно без совершенствования и автоматизации процесса проектирования, применения новых материалов и технологий.

Необходимость внедрения в производство сложнейшей техники в короткие сроки приводит к созданию систем автоматизированного проектирования. Важную роль в этих системах играет расчет на прочность.

В основе любого расчета на прочность лежит расчетная схема, включающая в себя геометрию конструкции и действующие на нее нагрузки (механические и температурные). В дальнейшем, в зависимости от конечных целей расчета, используя те или иные модели материала конструкции, определяются напряжения и деформации элементов конструкции. Затем на основе анализа поля напряжений устанавливается наиболее опасное сечение, при этом используются те или иные гипотезы прочности, в зависимости от свойств материала и условий работы конструкции.

Естественно, что при создании расчетной схемы сложной конструкции прибегают к некоторой идеализации ее формы, при этом степень этой идеализации влияет на достоверность результатов расчета.

Теории упругости и пластичности, теория пластин и оболочек и другие аналитические теории решают большое количество технических задач, связанных с исследованием напряженно-деформированного состояния твердых тел. Тем не менее, многие практически важные технические задачи не могут быть решены аналитически вследствие сложности геометрии конструкции и граничных условий. Так, например, конструкции с простой геометрией (рис. 6.1, а - в) могут быть решены аналитически для получения значений внутренних напряжений, смещений, частот собственных колебаний.

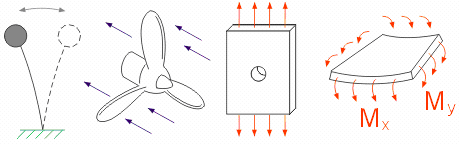
Рис. 6.1. Примеры анализируемых конструкций

Задачи со сложной геометрией (например, гребной винт рис. 6.1, г) обычно решаются численными методами, к которым относится, в частности, и метод конечных элементов.

Стремление рассмотреть все более близкие к действительности форму и условия работы конструкции, а также стремление учесть реальные особенности деформирования материала потребовало дальнейшего совершенствования численных методов расчета.

Рассмотрим более подробно основные этапы численного исследования, прочности конструкций: построение физической модели, построение математической модели, методы исследования математической модели и анализ полученных результатов.

6.1.1. Построение физической модели

Построение физической модели включает в себя идеализацию свойств конструкции и внешних воздействий.

В общем случае конструкция, изготовленная из реального материала, находящаяся под действием внешних нагрузок, может иметь много особенностей, включающих в себя несовершенство формы, несплошность и неоднородность свойств материала, особенности в характере внешнего нагружения и т. п. В практических расчетах учесть все имеющиеся особенности конструкции, материала и нагружения невозможно. Конечно, привлечение ЭВМ расширило возможности учета в прочностных расчетах некоторых из перечисленных выше особенностей, но необходимо понимать, что как бы ни были велики мощности современных ЭВМ, их быстродействие и объем памяти, но и они не безграничны. Поэтому, приступая к практическим расчетам, мы вынуждены подменять реальные тела некими которыми идеализированными объектами - «механическими моделями». В качестве примера кратко рассмотрим эволюцию модели одного из основных объектов механики - сплошной среды. В курсах теоретической механики вводится понятие материальной точки, как некоторого идеализированного (несуществующего в природе) объекта, имеющего массу, но не имеющего размеров. Подобная идеализация оказалась достаточной для решения целого ряда задач. Например, при изучении движения планет вокруг Солнца достаточно считать Солнце и движущиеся вокруг него планеты материальными точками, т. к. расстояние между планетами и Солнцем гораздо больше размеров самих небесных тел.

Далее, реальное твердое тело или жидкость можно представить себе как бесконечную систему материальных точек, определенным образом взаимодействующих между собой. С точки зрения атомного строения вещества и существования сил межатомного взаимодействия каждой из материальных точек свойственна определенная индивидуальность. Однако проследить за состоянием каждой из материальных точек совершенно невозможно, поэтому приходится вводить некоторые осредненные характеристики, описывающие взаимодействие между атомами, отказавшись от рассмотрения каждого атома в отдельности (статистическая физика). Методы статистической физики хорошо развиты применительно к газам. Для описания поведения твердых тел сведения об их атомной структуре не нужны. Реальное твердое тело заменяется воображаемой (модельной) сплошной средой. Среда называется сплошной, если любой объем, выделенный из нее, содержит вещество. Такое представление о сплошной среде противоречит представлению об атомном строений, вещества, однако оно чрезвычайно упрощает математическое описание поведения твердых тел под действием приложенной нагрузки.

Еще одной идеализацией реального твердого тела является присвоение ему свойств однородности. Среда называется однородной, если свойства выделенных из нее малых объемов одинаковы. Естественно, здесь речь идет о тех свойствах, которые определяются посредством механического эксперимента. Однако известно, что обычный металл или сплав состоит из кристаллических зерен, ориентированных случайным образом. Очевидно, что свойства этих объемов могут быть различными, т.к. металл неоднороден в пределах зерна. Но наличие этих неоднородностей не влияет на поведение металла в изделии, поскольку размеры этих зерен малы по сравнению с размерами изделия, и подобный металл рассматривается как однородная сплошная среда.

Существуют неоднородные материалы с размером неоднородности значительно большим, чем у металлов, например, бетон. Но и изделия из таких материалов имеют размеры, по сравнению с которыми размеры структурных элементов пренебрежимо малы.

В ряде конструкций такая идеализация невозможна, т. к. она привела бы к неверным результатам расчета. Примером может служить пластинка из биметалла, в которой свойства меняются скачкообразно при переходе границы раздела материалов. Свойства неоднородного материала могут также меняться непрерывно по объему. Примером этого является неравномерно нагретое тело, в котором свойства материала зависят от температуры, распределенной по объему непрерывным образом (или с конечным числом разрывов).

Определенной идеализации подвергается также и понятие «внешние силы». В механике предполагается, что сила полностью определена, если задан соответствующий вектор, при этом сила рассматривается как результат взаимодействия двух твердых тел. С этой точки зрения вектор силы, действующей на поверхность тела, означает сосредоточенную силу, т. е. силу, приложенную в точке. Однако, в действительности, «сосредоточенных» сил не существует.

Идеализированное понятие о точечном контакте двух твердых тел неразрывно связано с идеализацией твердого тела как абсолютно жесткого. При контакте реальные твердые тела деформируются, образуя площадку контакта конечных размеров, по которой давление распределяется непрерывно и неравномерно. Однако у достаточно прочных материалов размеры площадки контакта значительно меньше остальных размеров конструкции, поэтому при расчете напряженно-деформированного состояния (НДС) элементов конструкции вдали от площадки контакта ввод идеализированной сосредоточенной силы вполне оправдан. Но при расчете НДС вблизи этой площадки замена распределенного давления сосредоточенной силой приводит к значительным погрешностям.

Таким образом, физическая модель может быть наделена лишь частью свойств реальной конструкции, а поэтому - проще ее математическое описание. От того, насколько удачно выбрана физическая модель конструкции, зависит, в конечном итоге, трудоемкость расчета и точность его результатов. Здесь многое зависит от опыта расчетчика, его понимания работы конструкции, умения выделить те характеристики, которые, в основном, и определяют ее работу.

6.1.2. Построение математической модели

Следующим этапом расчета является математическое описание поведения модели, или построение математической модели. В самых общих чертах она включает в себя входные и выходные данные и математически сформулированный оператор перехода от первых ко вторым.

При математическом описании поведения модели часто приходится вводить дополнительные упрощающие предположения о характере отдельных свойств модели и ее мате­риала. Этим объясняется, в частности, существование для одной и той же физической мо­дели нескольких различных математических моделей. Так, например, если задачей расчета балки из изотропного материала на изгиб является определение лишь нормальных напряжений, в основу математической теории изгиба достаточно положить гипотезу плоских сечений, по которой плоские до деформации поперечные сечения балки остаются и после деформации плоскими и ортогональными к изогнутой оси (техническая теория, или теория Бернулли - Эйлера). Однако точная теория, построенная Сен-Венаном для изгиба балки сосредоточенными силами, показывает, что, хотя гипотеза плоских сечений и не соблюдается, полученные на ее основе результаты весьма точны для балок, длина которых гораздо больше размеров ее сечения. В то же время, как известно из технической теории изгиба, введение гипотезы плоских сечений позволило описывать деформированное состояние балки при помощи небольшого числа параметров.

Для перехода к напряжениям в технической теории изгиба понадобилось еще сделать предположение об отсутствии взаимодействия между слоями, параллельными оси балки.

При математическом описании поведения изотропных пластин также используется ряд гипотез: прямых нормалей, прямой линии, о равномерном распределении касательных напряжений по толщине пластины и т. п.

6.1.3. Метод исследования математической модели и анализ полученных результатов

Часто для математической модели может существовать несколько методов ее исследования. Так, например, дифференциальное уравнение

[ЕI(x) ''(x)]'' - T ''(x) + k(x)  (x) = q(x)

при некоторых краевых условиях образует мате магическую модель изгиба непризматической балки с изгибной жесткостью ЕI(x), лежащей, на упругом основании переменной жесткости k(x) и подверженной действию поперечной нагрузки интенсивностью q(x) и осевых сил Т (рис. 1.2).

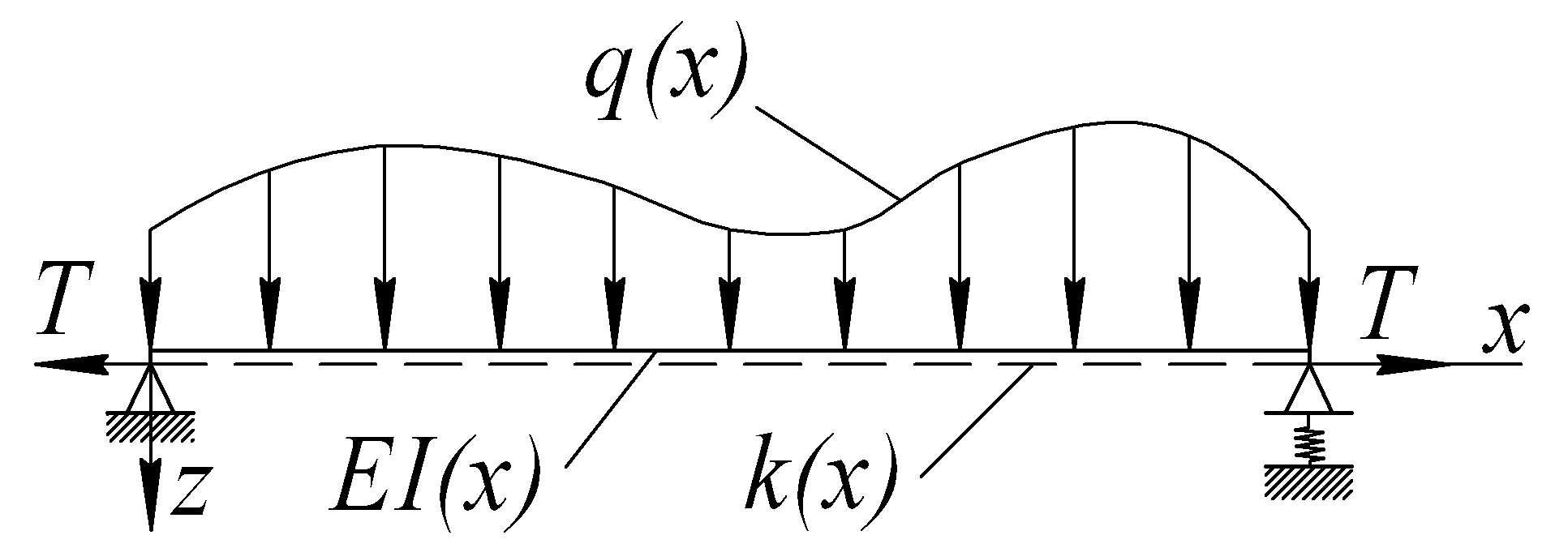
Рис. 6.2. Схема балки

Исследовать данную математическую модель, т. е. получить решение дифференциального уравнения при заданных граничных условиях, можно с помощью обобщенного метода начальных параметров, метода Ритца, метода сеток, метода коллокаций, метода конечных элементов и т. д. Выбор метода исследования математической модели может существенно сказаться на устойчивости алгоритма - чувствительности результата решения к неизбежным погрешностям числовых операций. Например, при расчете достаточно длинной балки, лежащей на упругом основании, использование метода начальных параметров может привести к числовой неустойчивости и большим погрешностям результатов. В то же время использование метода прогонки приводит к устойчивому числовому алгоритму.

6.2. Матричная форма записи основных соотношений теории упругости

В результате воздействия на тело внешних нагрузок и температуры его точки могут переместиться относительно друг друга в новые положения. В этом случае вектор перемещений для трехмерной задачи можно записать следующим образом: {u}={u_x, u_y, u_z}, где u_x, u_y, u_z (или соответственно u, ν, w) – проекции вектора перемещений на координатные оси х, у, z соответственно. Для двумерной задачи вектор перемещений имеет два компонента {u}={u_x, u_y}.

Разность перемещений двух соседних точек вызывает в материале деформации и связанные с ними напряжения. В общем случае деформации и напряжения в материале состоят из 6 компонент (рис. 6.3): σ_х, σ_у, σ_z, τ_ху, τ_уz, τ_zx – для напряжений и ε_х, ε_у, ε_z, γ_ху, γ_уz, γ_zx – для деформаций.

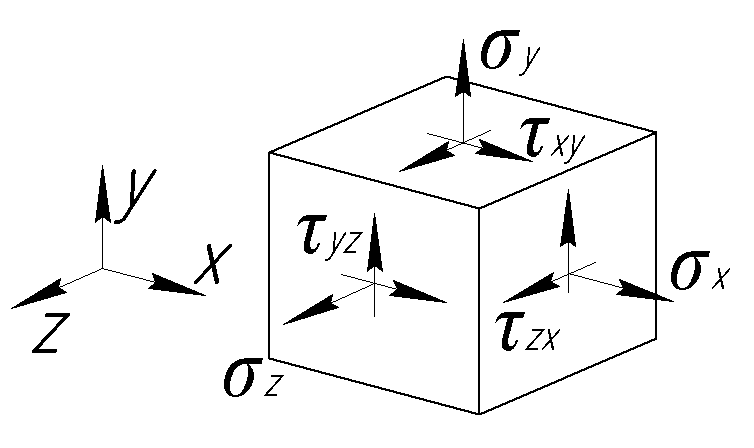
Рис. 6.3.

Расчет задачи в трехмерной (объемной) постановке требует значительных компьютерных ресурсов, поэтому часто трехмерную схему приводят к двумерной используя понятия плоскодеформированного и плосконапряженного состояний.

Под плоским напряженным состоянием понимают случай σ_z = τ_уz = τ_zx =0 (ε_z ≠0). Примером этого может служить плоское тонкое кольцо постоянной толщины, находящееся под действием давления (рис. 6.4, а).

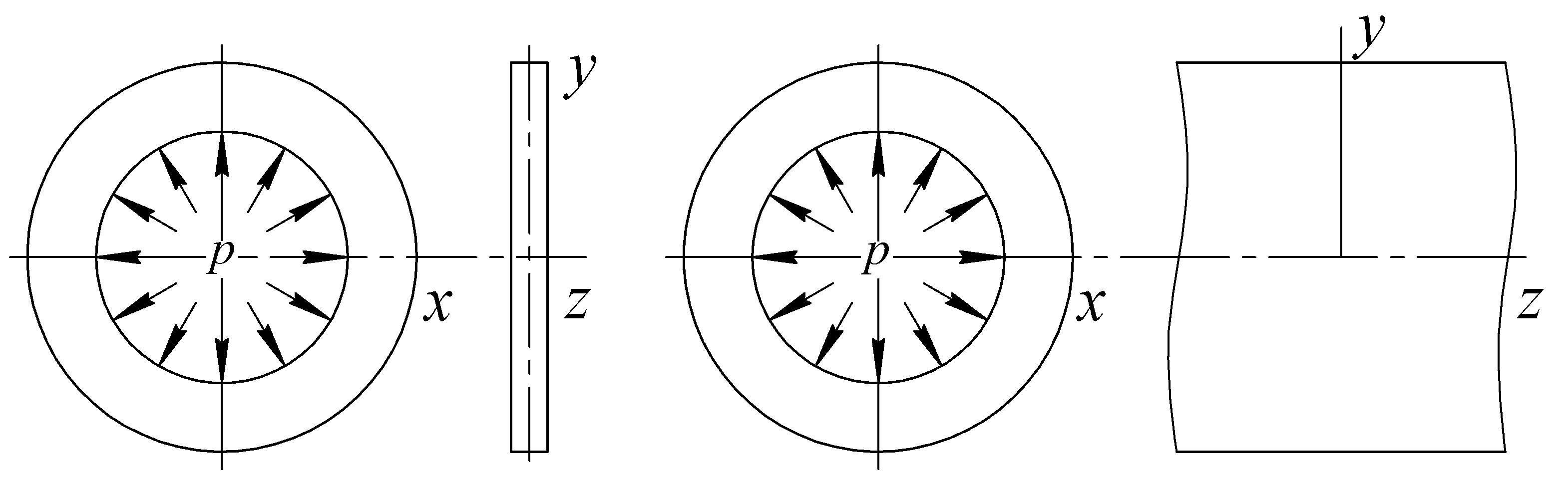
а б

Рис. 6.4. Схемы плосконапряженного (а) и плоскодеформированного (б) состояния

О плоской деформации говорят в случае ε_z = γ_уz = γ_zx =0 (σ_z ≠0). Примером может служить длинный цилиндр с постоянной площадью сечения под действием постоянного вдоль оси z внутреннего давления (рис. 6.4, б).

Основные соотношения между напряжениями, деформациями и температурой для упругих изотропных материалов могут быть записаны в виде:

,

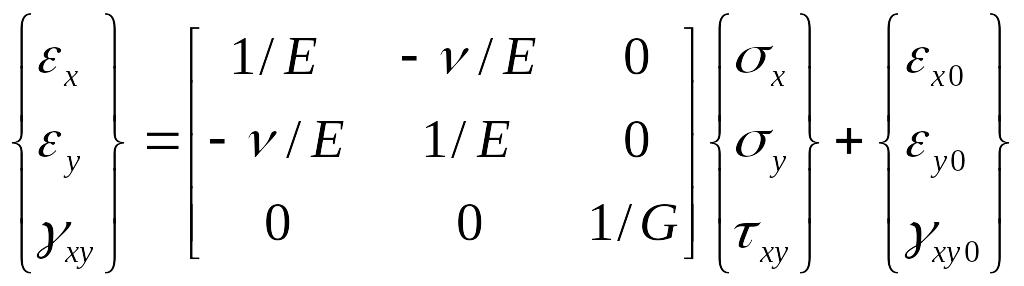или {ε}=[E]^-1∙{}+{ε₀}, где ε₀ – начальные деформации, Е - модуль упругости, ν - коэффициент Пуассона, G - модуль сдвига. Заметим что G = 0,5E/(1+ν). Анализ этого уравнения показывает, что для однородных изотропных материалов механическое состояние материала описывается двумя независимыми константами.

Решив приведенную систему уравнений, получим зависимость напряжений от деформаций:

,

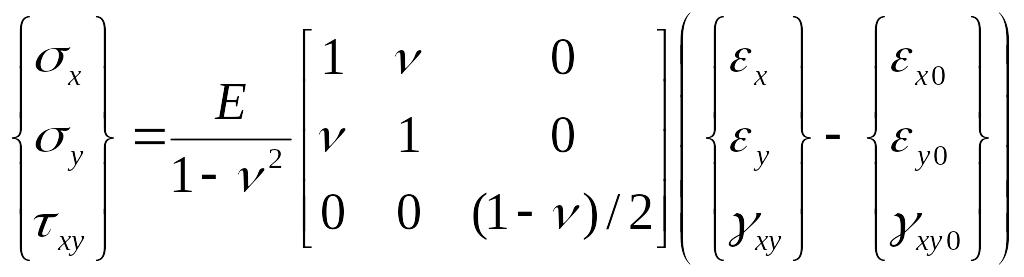или {}=[E]∙{ε}+{₀}, где {₀}= -[E]∙{ε₀} – начальные напряжения.

Приведенные выше формулы справедливы для случая плоского напряженного состояния. При плоской деформации выражения для постоянных материала необходимо изменить следующим образом:

EE/(1- ν²); ν  ν/(1- ν).

Связь между напряжениями и деформациями для случая плоской деформации выглядит следующим образом:

.

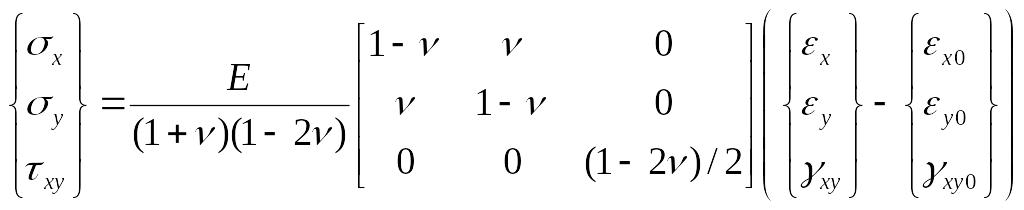Начальные напряжения вследствие изменения температуры определяются по формуле:

,

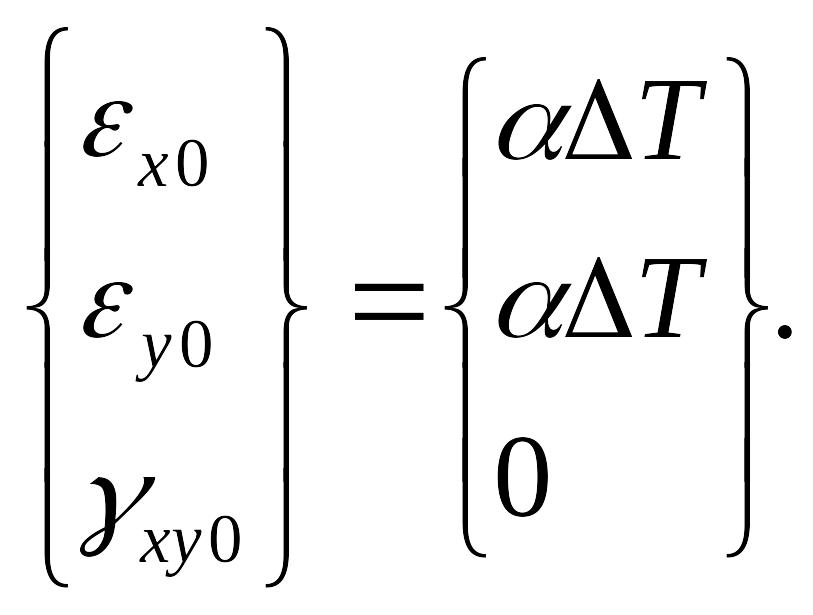где α – коэффициент линейного расширения при нагреве, Т - изменение температуры. Если температурные деформации не стеснены, то при изменении температуры в конструкции не возникают термические напряжения.

Для малых деформаций и перемещений имеют место следующие зависимости: ε_х = u/x, ε_y = ν/y , γ_ху = u/y + ν/x, или в матричной форме

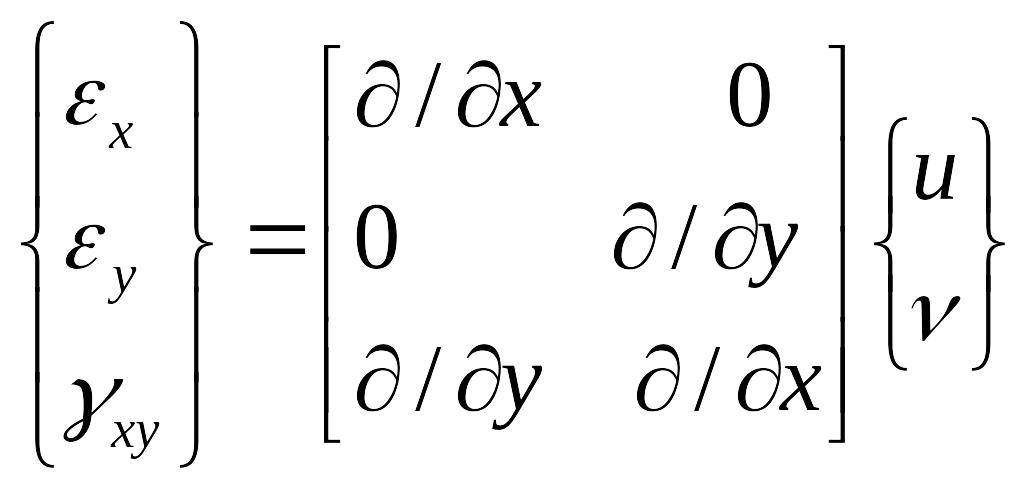, или { ε }=[D]∙{u}.

Согласно теории упругости, напряжения в элементе объема должны удовлетворять уравнениям равновесия:

σ_х/x+τ_ху /у+ f_x =0, τ_ху /x+σ_у/у+ f_x =0,

где f_x, f_y – удельная сила (например, сила тяжести или инерции) на единицу объема.

Воздействие на тело внешних сил в МКЭ представляют в виде граничных условий, в качестве которых могут выступать силовые факторы (распределенные поверхностные нагрузки, объемные силы, сосредоточенные силы, моменты и т.д.) или закрепления (ограничение подвижности вдоль направления или вращения вокруг оси). Все виды нагрузок приводят к сосредоточенным нагрузкам, приложенным в узлах.

6.3. Идея и область применения МКЭ

6.3.1. Основные понятия

Возникновение МКЭ связано с решением задач космических исследований (1950 г.). Этот метод возник из строительной механики и теории упругости, а уже потом был осмыс­лен математиками, которые часто называют данный метод вариационно-разностным, под­черкивая тем самым его математическую природу. Они занимаются математическим обос­нованием МКЭ, т. е. проводят теоретический анализ его сходимости и точности резуль­татов. Представители же инженерного направления решают довольно сложные технические задачи, часто не задумываясь над строгим обоснованием применяемых ими приемов, а построенные алгоритмы и программы проверяют на известных точных решениях.

Существенный толчок в своем развитии МКЭ получил после того, как было доказано (1963 г.), что этот метод можно рассматривать как один из вариантов известного в строительной механике метода Рэлея-Ритца, который путем минимизации потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия.

Связь МКЭ с процедурой минимизации позволила широко использовать его при решении задач в других областях техники. Метод применялся к задачам, описываемым Уравнениями Лапласа или Пуассона (например, электромагнитные поля). Решение этих уравнений также связано с минимизацией некоторого функционала. Известны решения с помощью этого метода задач распространения тепла, задач гидромеханики и, в частности задач о течении жидкости в пористой среде.

Область применения МКЭ существенно расширилась, когда было показано (1968 г.) что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёркина или способ наименьших квадратов. Установление этого факта сыграло важную роль в теоретическом обосновании МКЭ, т. к. позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов из численной процедуры решения задач строительной механики превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. Этот прогресс был достигнут за довольно короткий срок, благодаря совершенствованию быстродействующих ЭВМ.

Кратко изложим сущность МКЭ и основные этапы его практической реализации. Основная идея метода конечных элементов состоит в том, что любую непрерывную величину (перемещение, температура, давление и т. п.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента.

В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что известны числовые значений этой величины в некоторых внутренних точках области (в дальнейшем эти точки мы назо­вем «узлами»). После этого можно перейти к общему случаю.

Чаще всего при построении дискретной модели непрерывной величины поступают следующим образом:

1. Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

2. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

3. Значение непрерывной величины в каждой узловой точке первоначально считается известным, однако необходимо помнить, что эти значения в действительности еще предстоит определить путем наложения на них дополнительных ограничений в зависимости от физической сущности задачи.

4. Используя значения исследуемой непрерывной величины в узловых точках и ту или иную аппроксимирующую функцию, определяют значение исследуемой величины внутри области.

Поясним сказанное выше на примере исследования распределения температуры в стержне. В общем случае распределение температуры неизвестно, и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Первоначально считают значения температуры в некоторых точках в пределах стержня известными. Определяют множество узлов и значения температуры в этих узлах, которые теперь являются переменными, т. к. они заранее неизвестны. Область (в нашем случае - длина стержня) разбивается на элементы, для каждого из которых определяется, аппроксимирующая функция. Узловые значения температуры должны быть теперь «выбраны» таким образом, чтобы с учетом граничных условий (например, значений температуры на концах стержня) обеспечить наилучшее приближение к истинному распределению температуры вдоль стержня. Этот «выбор» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функция, связанная с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений температуры. В прочностных задачах, где определяются поля перемещений, деформаций и напряжений, минимизируется потенциальная энергия деформированного тела.

Аппроксимирующие функции чаще всего выбираются в виде линейных, квадра­тичных или кубических полиномов. Для каждого элемента можно подбирать свой полином, но полиномы подбираются таким образом, чтобы сохранить непрерывность величины вдоль границ элемента. Этот полином, связанный с данным элементом, называют «функцией элемента».

С этой точки зрения конструкцию можно рассматривать как некоторую совокупность конструкционных элементов, соединенных в конечном числе узловых точек. Если известны соотношения между силами и перемещениями для каждого отдельного элемента, то, используя известные приемы строительной механики, можно описать свойства и исследовать поведение конструкции в целом.

В сплошной среде число точек связи бесконечно, и именно это составляет основную трудность получения численных решений в теории упругости. Понятие «конечных элементов» представляет собой попытку преодолеть эту трудность путем разбиения сплошного тела на отдельные элементы, взаимодействующие между собой только в узловых точках, в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. Если такая идеализация допустима, то задача сводится к обычной задаче строительной механики, которая может быть решена численно.

Таким образом, при использовании МКЭ решение краевой задачи для заданной области ищется в виде набора функций, определенных на некоторых подобластях (конечных элементах).

6.3.2. Основные этапы практической реализации

Как было отмечено ранее, согласно МКЭ, модель конструкции сложной формы подразделяется на более мелкие части (конечные элементы) сравнительно простой формы, в пределах которых ищется приближенное решение. Результатом такого моделирования обычно является поле напряжений и смещений в целой конструкции.

Таким образом, решение задачи с применением МКЭ состоит из следующих основных этапов (рис. 6.5):

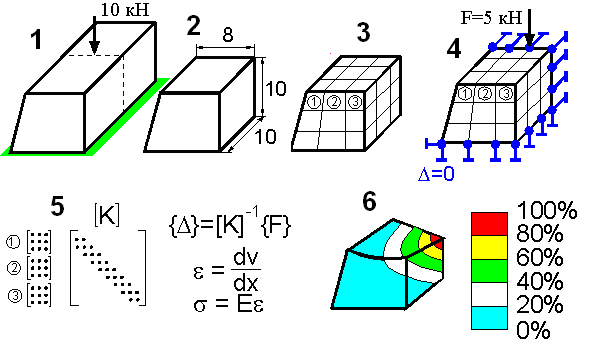
Рис. 6.5. Этапы реализации МКЭ

1) идентификация задачи, присвоение ей имени; создание чертежа конструкции и нагрузок;

2) создание геометрии модели, пригодной для МКЭ;

3) разбиение модели на сетку конечных элементов;

4) приложение к модели граничных условий (закрепление на границе или граничные нагрузки);

5) численное решение системы уравнений (автоматически);

6) анализ результатов.

Этапы 1, 2, 3, 4 относятся к препроцессорной стадии, этап 5 - к процессорной стадии, этап 6 - к постпроцессорной стадии.

Построенная модель делится на конечные элементы достаточно простой формы. Имеются несколько типичных форм конечных элементов, в которых поле смещений определяется по смещениям узлов с помощью некоторых интерполяционных функций. По вычисленным таким образом смещениям определяются поля напряжений и деформаций.

Наиболее трудоемкий этап решения задач с помощью МКЭ - это создание конечно - элементной модели на стадии препроцессорной подготовки, т. к. автоматическое построение сетки элементов не гарантирует от появления ошибок. Правильное приложение нагрузок и граничных условий также представляет определенные трудности.

Пятый из перечисленных выше этапов (численное решение системы уравнений) выполняется автоматически и, как правило, особых трудностей не вызывает (за исключением систем с плохо обусловленной матрицей жесткости).

Шестой этап (анализ результатов) существенно облегчается имеющимися мощными инструментальными средствами визуализации результатов.

Учитывая то, что в конечно-элементных задачах неизвестными являются перемеще­ния в узлах, а также то, что в трехмерных задачах каждый узел тетрагонального элемента может иметь перемещения по трем направлениям (рис. 6.6), система уравнений равновесия, записанная в матричной форме, может иметь размерность, достигающую 100000 и более. Однако для современных ЭВМ решение таких систем уравнений - вполне посильная задача. При составлении уравнений равновесия учитывается, что сумма проекций всех сил на каждую из координатных осей равна нулю, а сумма внутренних сил равна внешней силе с обратным знаком.

Рис. 6.6.

В трехмерных моделях число узлов обычно больше числа элементов, а число степеней свободы в 3 раза больше числа узлов (за исключением числа кинематических граничных условий).

Матрица жесткости [К] связывает векторы узловых смещений {U} и нагрузок {F}. Матрица жесткости является симметричной диагональной матрицей, что существенно облегчает ее обработку.

6.3.3. Конечные элементы

Как следует из основной концепции МКЭ, вся модель конструкции (или отдельной ее части) делится на множество конечных элементов, соединенных между собой в вершинах (узлах) (рис. 6.7, а, б). Силы действуют в узлах. Конечный элемент не является «абсолютно жестким» телом.

Конечно-элементная модель предполагает, что напряжения и деформации имеются и вне данного конечного элемента.

Имеются несколько наиболее употребительных типов конечных элементов (рис. 6.7, в): брус (А), стержень (В), тонкая пластина или оболочка (С), двумерное или трехмерное тело (D). Естественно, что при построении модели могут быть использованы не один, а несколько типов элементов.

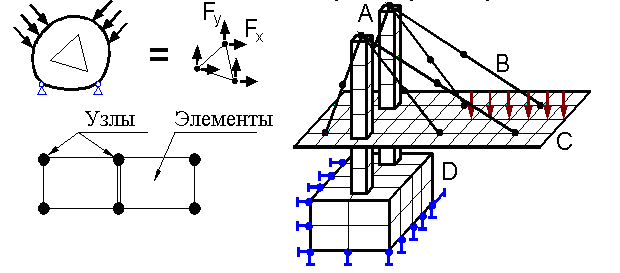
Рис. 6.7.

Достоверность расчетов по МКЭ зависит от многих факторов, в том числе и от коли­чества конечных элементов. Однако, если напряжения не меняются значительно в пределах модели, то количество конечных элементов несущественно влияет на точность вычисления напряжений.

Конечные элементы могут быть линейными (элементы первого порядка) или параболическими (элементы второго порядка) (рис. 6.8).

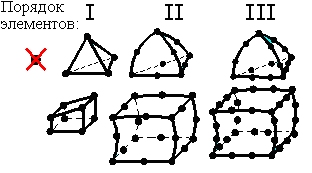
Рис. 6.8. Типы КЭ

Линейные элементы имеют прямые стороны и узлы только в углах. Таким образом, минимальное число узлов трехмерного элемента равно 4. Параболические элементы могут иметь промежуточный узел вдоль каждой из сторон. Именно благодаря этому стороны элемента могут быть криволинейными (параболическими). При равном количестве элементов параболические элементы дают большую точность вычислений, т. к. они более точно воспроиз­водят криволинейную геометрию модели и имеют более точные функции формы (аппроксимирующие функции). Однако расчет с применением конечных элементов высоких по­рядков требует больших компьютерных ресурсов и большего машинного времени.

Рассмотрим самый простой трехмерный линейный элемент с 8 узлами (рис. 6.9). Каждый из узлов имеет 3 степени свободы. Это означает, что необходимо рассмотреть 24 узловые смещения и столько же узловых сил. Таким образом, размерность матрицы жесткости [К], связывающей вектор узловых смещений с вектором узловых сил, будет [24  24].

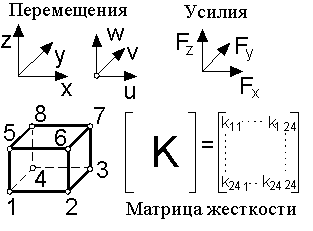
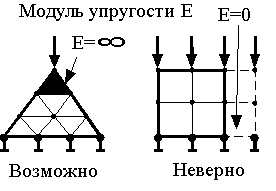
Рис. 6.9 Рис. 6.10

Компоненты матрицы жесткости прямо пропорциональны модулю упругости. Таким образом, нулевой модуль упругости означает отсутствие конечного элемента (рис. 6.10). В этом случае деление на нулевой модуль упругости приведет к значительным погрешностям.

Бесконечно большой модуль упругости означает, что данный элемент является абсолютно жестким. Кроме того, если теория упругости допускает бесконечные напряжения (например, в вершине трещины), то в МКЭ напряжения всегда конечны.

Несколько замечаний относительно соотношения между сторонами элемента. «Длинные» элементы с соотношением сторон 2 и более (рис. 6.11) можно использовать, если не ожидаются большие градиенты смещений, деформаций и напряжений, т. е. вдали от зоны действия концентраторов напряжений.

Если конструкция и нагрузки симметричны относительно оси, как показано, например, на рис. 6.12, задача может быть решена с помощью плоских симметричных конечных элементов.

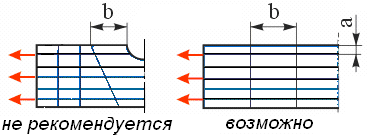
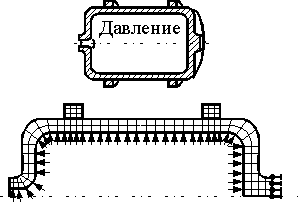
Рис. 6.11. Рис. 6.12.

6.3.4. Построение сетки конечных элементов

Одним из наиболее важных этапов в конечно-элементном анализе является построение на модели сетки из конечных элементов, т. е. разделение всей модели на маленькие кусочки (конечные элементы), связанные между собой в узлах.

Существуют два основных метода построения сетки построение произвольной сетки (рис. 6.13, а) и построение упорядоченной сетки (рис. 6.13, б).

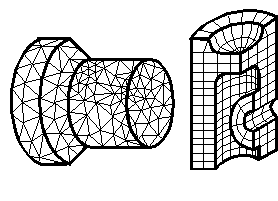
Рис. 6.13 Рис. 6.14

Произвольная сетка строится автоматически, при этом соседние элементы могут существенно отличаться по размерам. Упорядоченная сетка строится путем деления геометрических элементов модели на некоторое число частей. В автоматически построенных сетках с большим числом элементов число узлов преобладает над числом элементов. Отношение между узлами и элементами, примерно, 2:1 для плоских, произвольных сеток и 6:1 для произвольных трехмерных сеток с четырехгранными элементами.

Очевидно, что чем меньше линейный размер конечного элемента Н (рис. 6.14), тем большее количество элементов в модели, при этом время вычислений существенно возрастает, а ошибки анализа уменьшаются. Однако, ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ.

Практика расчетов с применением МКЭ позволяет дать следующие рекомендации (рис. 6.15): 1) линейные элементы требуют более частой сетки, чем квадратичные элементы (с одним промежуточным узлом) или кубичные (с двумя промежуточными узлами), 2) упорядоченная сетка (б) является более предпочтительной, чем произвольная сетка (о), 3) прямоугольная сетка с 4 узлами (в) более предпочтительна, чем сетка с треугольными элементами (б); 4) сетка треугольных элементов с промежуточными узлами (г) имеет, по крайней мере, ту же самую точность, что и сетка прямоугольных элементов с 4 узлами (в); 5) прямоугольная сетка с 8 узлами (д) является более предпочтительной, чем сетка тре­угольных элементов с промежуточными узлами (г), несмотря на больший размер прямоугольных элементов; 6) аппроксимация смещений кубическим полиномом (е) не требует более мелкой сетки.

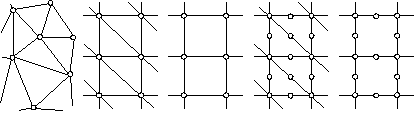
а б в г д

Рис. 6.15

Необходимо помнить, что МКЭ - приближенный метод, точность которого зависит от правильного выбора типов и размеров конечных элементов. Так, например, более частая сетка требуется там, где ожидается большой градиент деформаций или напряжений (рис. 6.16). В то же время более редкая сетка может применяться в зонах с более или менее постоянными деформациями или напряжениями, а также в областях, не представляющих особого интереса. В связи с этим исследователь должен уметь предвидеть области концентрации напряжений.

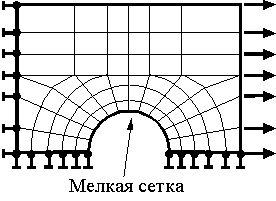
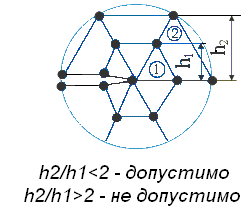
Рис. 6.16 Рис. 6.17

Необходимо заметить, что точность результатов анализа уменьшается, если размеры соседних элементов вблизи концентратора напряжений существенно различны (рис. 6.17).

Форма конечных элементов также влияет на точность вычислений. С этой точки зрения следует избегать слишком узких и вытянутых элементов (рис. 6.18), т. к. элементы с одинаковыми, примерно, сторонами дают меньшую ошибку.

Одновременно в сетке могут присутствовать треугольные и четырехугольные элементы, однако между ними не должно быть разрывов (рис. 6.19).

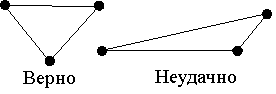
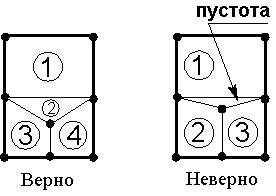
Рис. 6.18 Рис. 6.19

Для дальнейшего объединения элементов в сетку узлы последовательно нумеруются. Запрещается строить четырехугольные элементы с углами, большими 180⁰ (рис. 6.20).

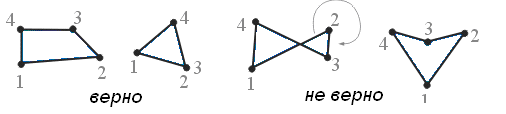
Рис. 6.20

6.3.5. Граничные условия

Задание граничных условий - один из ответственных этапов конечно-элементного анализа. Так, например, на модели, показанной на рис. 6.21, изображенные графически граничные условия в узлах А и В служат для того, чтобы перемещение указанных узлов модели соответствовали перемещениям тех же узлов натурной конструкции с учетом наложенных на них связями ограничений. При этом перемещения могут приобретать как нулевые (в узле А), так и не нулевые (в узле В) значения. Существуют также граничные условия, при которых задаются нагрузки (узел С).

Граничные условия (перемещения или силы) прикладываются только к узлам (рис. 6.22). Максимальное число граничных условия, приложенных в узле, равно числу степеней свободы – 3 силы или 3 перемещения.

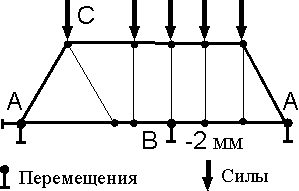
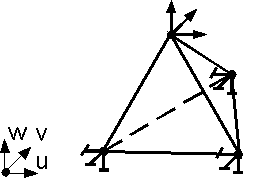
Рис. 6.21 Рис. 6.22

Необходимо обратить особое внимание на то, что число граничных условий должно быть минимально необходимым (не меньше и не больше). Так, например, не следует фиксировать все степени свободы (все перемещения) в каждом узле элемента (рис. 6.23, а); не следует также прикладывать силу в узле в том же самом направлении, в котором в данном узле зафиксировано смещение (рис. 6.23, б); полное отсутствие закрепления вдоль какой-либо из осей (рис. 6.23, в) может привести при анализе к кажущемуся сдвигу вдоль этой оси вследствие неизбежных ошибок округления при численных расчетах. Для рассмотренных примеров правильные схемы граничных условий показаны на рис. 6.23, г, д.

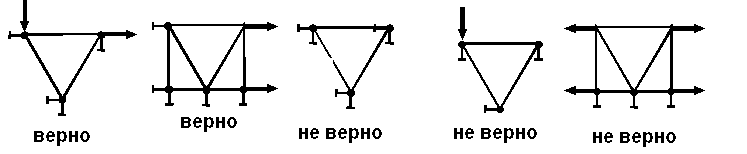
а б в г д

Рис. 6.23

Схема размещения граничных условий зависит от вида нагружения (растяжение, чистый изгиб, сдвиг), как показано на рис. 6.24.

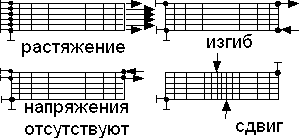
Рис. 6.24

Если конструкция имеет оси или плоскости симметрии, то при назначении граничных условий необходимо это учитывать. Так, например, пресс с жесткими пуансонами, сжи­мающий куб из более мягкого однородного материала (рис. 6.25, а), имеет три плоскости симметрии. Очевидно, в этом случае нет необходимости моделировать всю конструкцию целиком. Можно смоделировать только часть конструкции (1/4 или 1/8), имея в виду, что в точках на плоскостях симметрии соответствующие перемещения равны нулю. Это обстоятельство мы учитываем соответствующими граничными условиями в узлах элементов, лежащих на плоскостях симметрии (рис. 6.25, б).

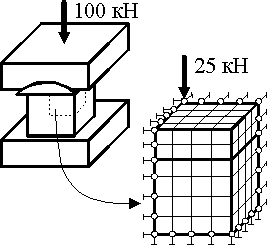
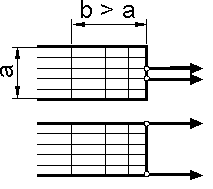
Рис. 6.25 Рис. 6.26

Выбор размеров элементов и граничных условий при построении сетки можно существенно упростить, если принять во внимание принцип Сен-Венана: две статически экви­валентные системы сил создают одно и то же поле напряжений на расстоянии от их точек приложения, большем, чем характерный линейный размер поперечного сечения (b>a, рис. 6.26).

Рассмотрим следующую ситуацию. Известно, что чрезмерно большие растягивающие напряжения являются основной причиной многих разрушений. В этом случае, если зона максимальных растягивающих напряжений находится вдали от точки приложения силы (например, как на схеме рис. 6.27), нет необходимости строить подробную сетку элементов вблизи этой точки, т. к. здесь действуют, в основном, сжимающие напряжения.

Рис. 6.27

6.3.6. Точность результатов

Численный анализ, к которому относится и МКЭ, требует некоторой идеализации реальной конструкции. Поэтому, несмотря на мощное развитие вычислительной техники, результаты вычислений по МКЭ не свободны от ошибок Использование вычислительной техники в роли «черного ящика», без понимания основных процессов и этапов вычислений, может привести к существенным ошибкам. К сожалению, не исключены также и ошибки операторов.

Приступая к конечно-элементному анализу, инженер должен понять:

- к какой области анализа относится данная задача;

- какая часть всей конструкции должна исследоваться подробнее;

- какие упрощения можно допустить в данной задаче.

Естественно, это требует определенной квалификации исследователя.

Ошибки могут возникать на различных стадиях конечно-элементного анализа: при постановке задачи, дискретизации (построении модели), численном решении.

Ошибки постановки задачи могут возникать, когда выбранный тип конечных элементов или их размер не соответствуют физическому поведению материала в конструкции. Несколько уменьшить эту ошибку (по крайней мере, ту ее часть, которая связана с размером конечного элемента) можно, используя автоматическое построение сетки. Однако основным источником ошибок при постановке задачи является некорректное задание граничных условий. Таким образом, успех конечно-элементного анализа зависит от точности воспроизведения на модели граничных условий, геометрии и свойств материала натурной конструкции.

Ошибки дискретизации возникают при замене реальной конструкции ограниченным числом конечных элементов (с учетом их формы и размеров).

Ошибки, связанные с численным решением систем уравнений, обычно менее значимы, чем перечисленные выше два типа ошибок.

При конечно-элементном анализе, как правило, неизвестными являются смещения, и результатом решения в этом случае будет вектор смещений в узле {u}. Смещения в других точках элемента вычисляются интерполяцией.

После аппроксимации поля смещений (в пределах элемента) соответствующим полиномом, называемым «функцией формы», могут быть вычислены деформации и напряжения. Описанная схема вычислений показывает, что наибольшая точность достигается при определении смещений в узлах.

Деформации вычисляются дифференцированием соответствующих смещений, поэтому максимальная точность вычислений деформаций и напряжений будет в центре элемента. На рис. 6.28 показана деформированная частица для случая чистого изгиба. Как видим, теоретическое и численное решение совпадает в центральной части конечного элемента.

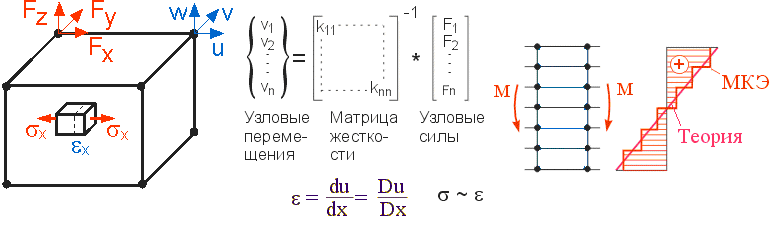
Рис. 6.28

Тип и количество элементов влияют на точность вычислений. Так, например, при вычислении силы в случае нелинейного анализа, при небольшом числе конечных элементов их количество существенно влияет на величину вычисляемой силы (рис. 6.29). Однако при увеличении числа элементов результаты стабилизируются.

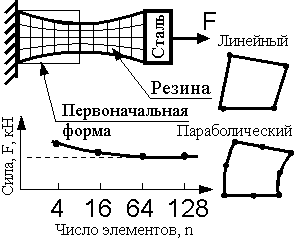
Рис. 6.29

Существуют два метода конечно-элементного анализа: h-метод (h - длина стороны конечного элемента) и p-метод (р - порядок полинома аппроксимирующей функции). Для повышения точности решения h-метод требует увеличения числа элементов. В соответствии с p-методом для увеличения точности надо повысить порядок полинома аппроксимирующей функции. Так, например, на рис. 6.30, б элементы более высокого порядка демонстрируют и большую точность результатов по сравнению с линейными элементами (рис 6.30, а).

На точность результатов влияет также и ориентация сторон элементов. Дня изгибаемой консольной балки увеличение числа элементов по высоте балки не дает повышения точности результатов (рис. 6.30, в). Гораздо лучшие результаты дает увеличение числа элементов второго порядка по длине балки (рис. 6.30, г).

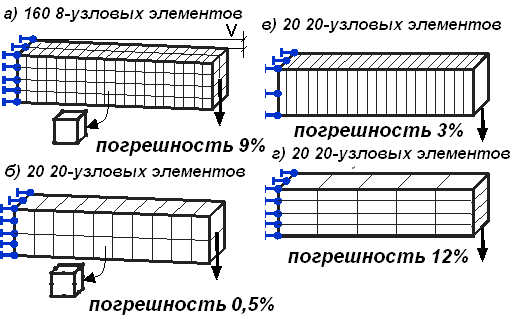
Рис.6.30

Для получения достоверных результатов в зонах концентрации напряжений размер элементов должен быть меньше. На рис. 1.33 показан фрагмент растягиваемой полосы с центральным отверстием. Известно, что максимальные напряжения действуют в сечении А-А, поэтому в окрестности данного сечения сетка элементов должна быть гуще, чем у левой границы полосы.

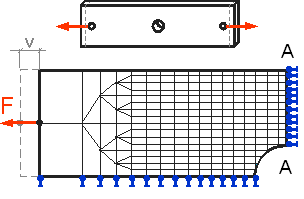
Рис. 6.31

6.4. Типы конечных элементов

Существует большое количество разнообразных типов конечных элементов (в программе ANSYS - около 100). На рис. 6.32 показаны лишь некоторые из них.

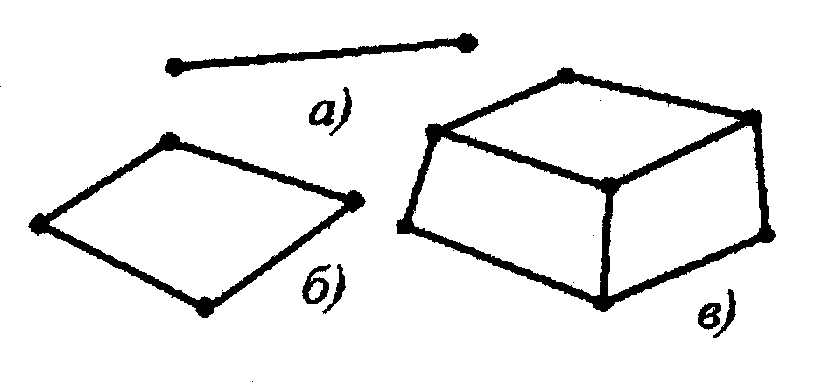
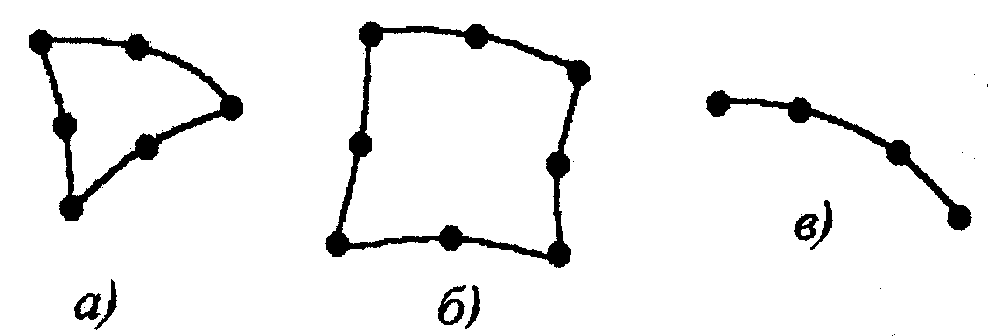
Рис. 6.32 Рис. 6.33

Задача разбиения тела на конечные элементы неоднозначна. В некоторых случаях (например, в случае расчета ферм) конструктивные элементы таковы, что совпадают с конечными элементами. Так, всю ферму можно моделировать линейными стержневыми элементами (рис. 6.32, а). Такими же элементами можно моделировать различного рода упругие конструктивные элементы (пружины, стержни, тяги и т. п.), а также системы трубопроводов. В этих случаях моделирование конструкции не представляет особого труда и состоит в выполнении некоторого объема работа по стандартным правилам. Гораздо сложнее выполнить эту операцию для двумерных или трехмерных областей. Здесь, прежде всего, нужно выбрать тип (или типы) конечных элементов (например, рис. 6.32, б, в), наилучшим образом аппроксимирующие исследуемую область. Плоские двумерные элементы (рис. 6.32, б) применяются, в основном, для моделирования мембран, тонких пластин, тонкостенных оболочек и т. п. Объемные трехмерные элементы (рис. 6.32, в) применяются, в основном, при исследовании полей температур, деформаций, напряжений в массивных телах и т. п.

На приведенном выше рис. 6.32 все элементы имеют прямые стороны, а узлы помещены на концах элемента (рис 6.32, а) или в вершинах углов (рис. 6.32, б, в). Таким образом, каждый элемент (или его сторона) ограничен соседними узлами и вся область будет аппроксимирована линейными элементами. Это наиболее простые элементы. Напомним, что значение искомой функции в узлах считается известным. Соответствующий этому элементу аппроксимирующий полином (функция элемента), определяемый по значениям функции в узловых точках элемента, будет линейным, т. к. он будет строиться по двум точкам.

Можно образовывать элементы с числом узлов вдоль одной стороны более двух (рис. 6.33). В этом случае введение одного или нескольких дополнительных узлов позволяет сделать стороны элементов криволинейными. Такие элементы являются более точными, т. к. функции элементов будут строиться уже не по двум, а по трем (рис. 6.33, а, б) или четырем (рис. 6.33, в) точкам и, следовательно, будут являться полиномами второй или третьей степени.

6.4.1. Линейный упругий элемент. Матрица жесткости

Начнем подробное рассмотрение типов конечных элементов с модели одного из простейших типов - упругого линейного элемента (например, упругой пружины), схема которого приведена на рис. 6.34.

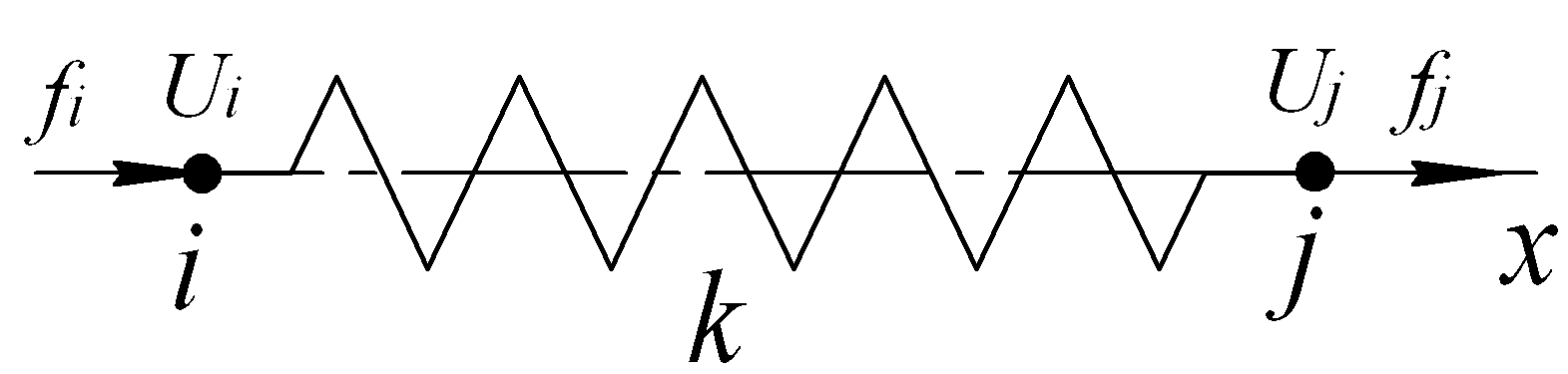
Рис. 6.34. Линейный упругий элемент

Элемент ограничен двумя узлами, обозначенными как i и j. В этих узлах приложены силы f_i и f_j [H], соответственно. Эти силы вызывают смещения узлов u_i и u_j [м]. Элемент характеризуется жесткостью k [Н/м], т.е. силой, необходимой для его деформации на единицу длины. Таким образом, зависимость силы от деформации запишется как f_i = k, где = u_j - u_i (удлинение элемента). При этом удлинение равно разности перемещений концов элемента (= u_j - u_i). Принято, что сила положительна, если ее направление совпадает с положительным направлением оси х.

Рассмотрим силы, действующие в узлах элемента:

в узле i: f_i = k(u_i - u_j);

в узле j: f_i = k(u_j - u_i),

или то же в матричной форме:

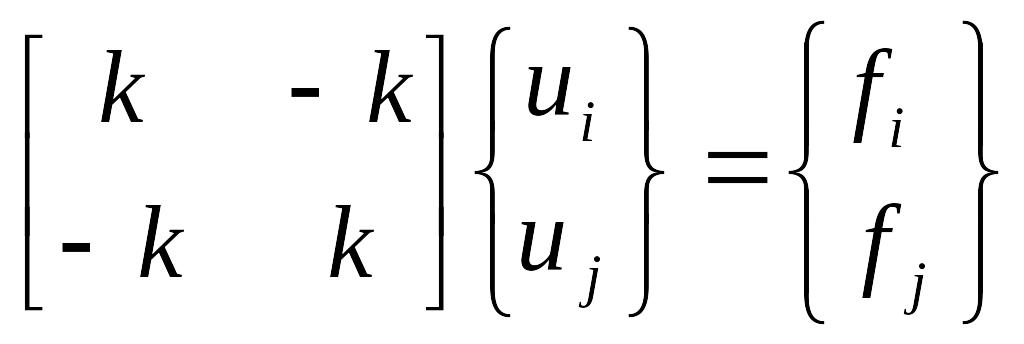, или ku=f. (6.1)

Здесь k - матрица жесткости; u - вектор смещений; f - вектор сил. Заметим, что матрица жесткости k - симметричная матрица.

6.4.2. Система упругих элементов. Матрица жесткости системы элементов

Рассмотрим систему из двух последовательно соединенных упругих элементов, схема которой приведена на рис. 6.35.

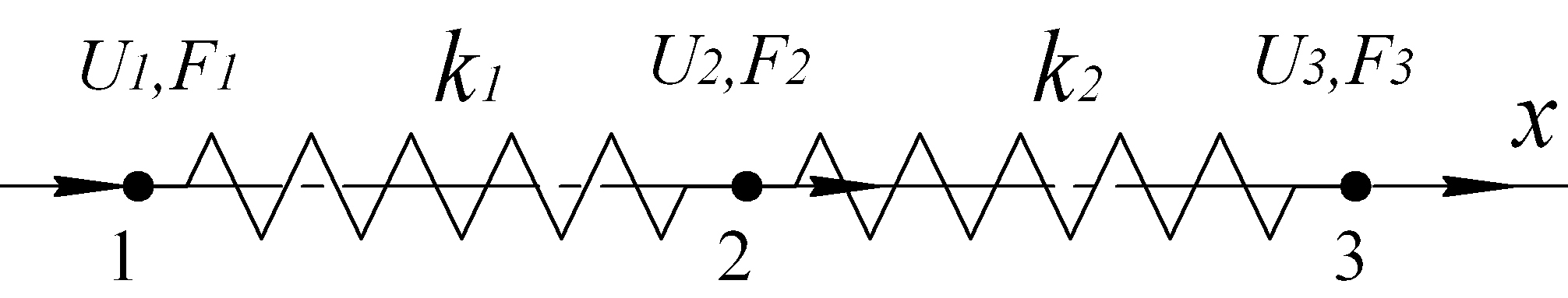
Рис. 6.35. Последовательная система упругих элементов

Для элемента 1, согласно (6.1) можно записать:

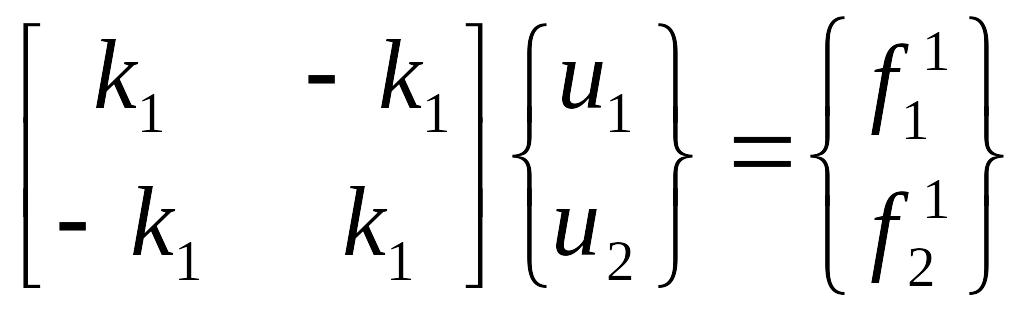
Аналогично для элемента 2:

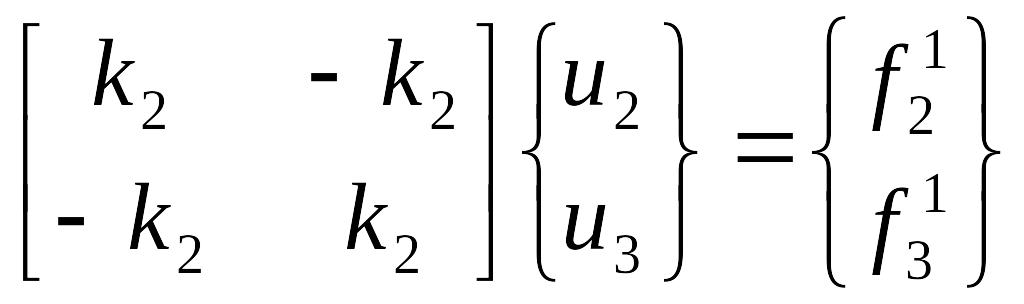
Здесь f_i^m внутренняя сила, действующая на i-й узел элемента m (i = 1, 2, 3; m = 1, 2). Поскольку на узел могут действовать несколько сил, то введем новое обозначение F_i для сил в узлах. Итак, на узлы действуют силы:

на узел 1: F₁ = f₁¹ ;

на узел 2: F₂ = f₂¹+ f₂²;

на узел 3: F₃ = f₃².

Для составления матрицы жесткости системы элементов рассмотрим равновесие сил, действующих на каждый из узлов:

F₁ = k₁u₁ - k₁u₂;

F₂ = - k₁u₁ + (k₁+ k₂)u₂ – k₂u₃;

F₃ = - k₂u₂ + k₂u₃;

или в матричной форме:

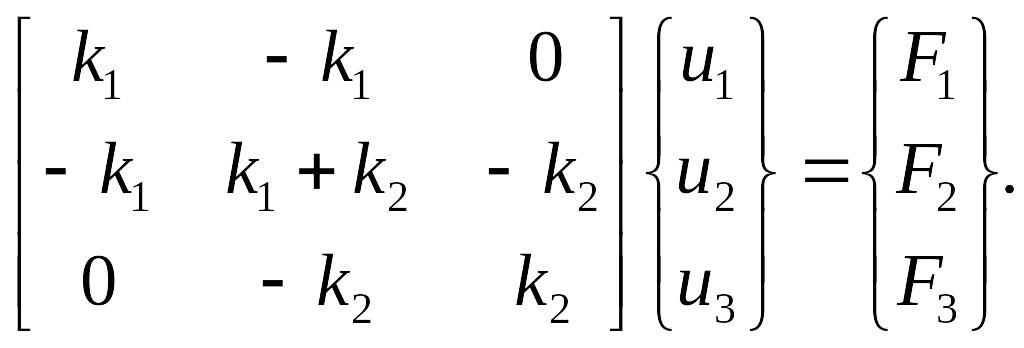(6.2)

где k - матрица жесткости системы элементов.

Из условий равновесия ясно, что если в узле нет внешней силы (реакции опоры), то для него F = 0. Одновременно укажем, что сумма сил в столбце F уравнений (6.2) равна нулю.

Для наглядного представления о способе получения матрицы жесткости системы элементов в приведенном выше матричном уравнении пунктирными линиями выделены матрицы жесткости 1 и 2 упругих элементов в отдельности. Видно, что так же, как и элементы в конструкции, матрицы жесткости элементов «сцеплены» в общем узле 2. Таким образом, главные диагонали матриц жесткости элементов совпадают с главной диагональю общей матрицы жесткости. Видно, что на диагонали стоят суммы жесткостей элементов, примыкающих к данному узлу.

Для введения граничных условий предположим, что узел 1 на рис. 6.35 жестко закреплен (в нем сила F₁ - реакция опоры), а в узлах 2 и 3 приложены силы Р. В этом случае u₁=0, F₂=F₃=P и мы получим:

.

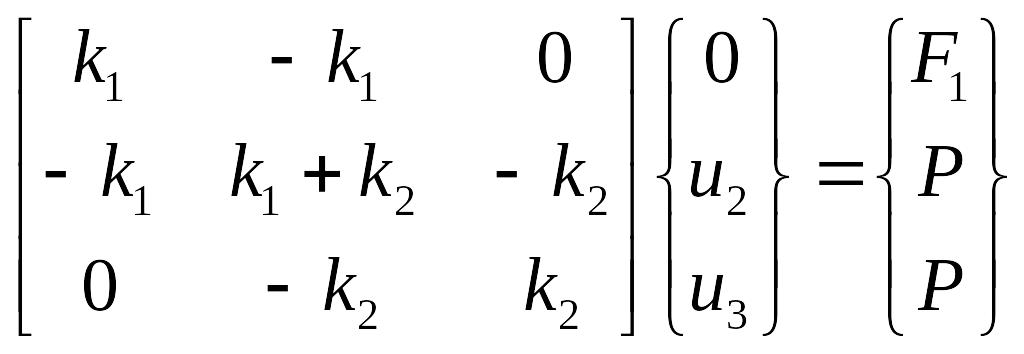Отсюда

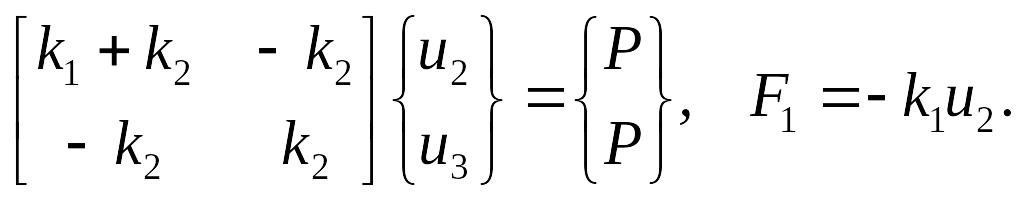
Здесь неизвестными являются F₁, u₂, u₃.

Решая приведенную выше систему уравнений, получим:

и₂ = 2P/k₁ ; u₃ =2P/k₁ + Р/к₂; F₃ = -2Р.

Рассмотрим ступенчатый стержень, изображенной на рис. 6.36, как систему из двух последовательно соединенных упругих элементов с жесткостями и .

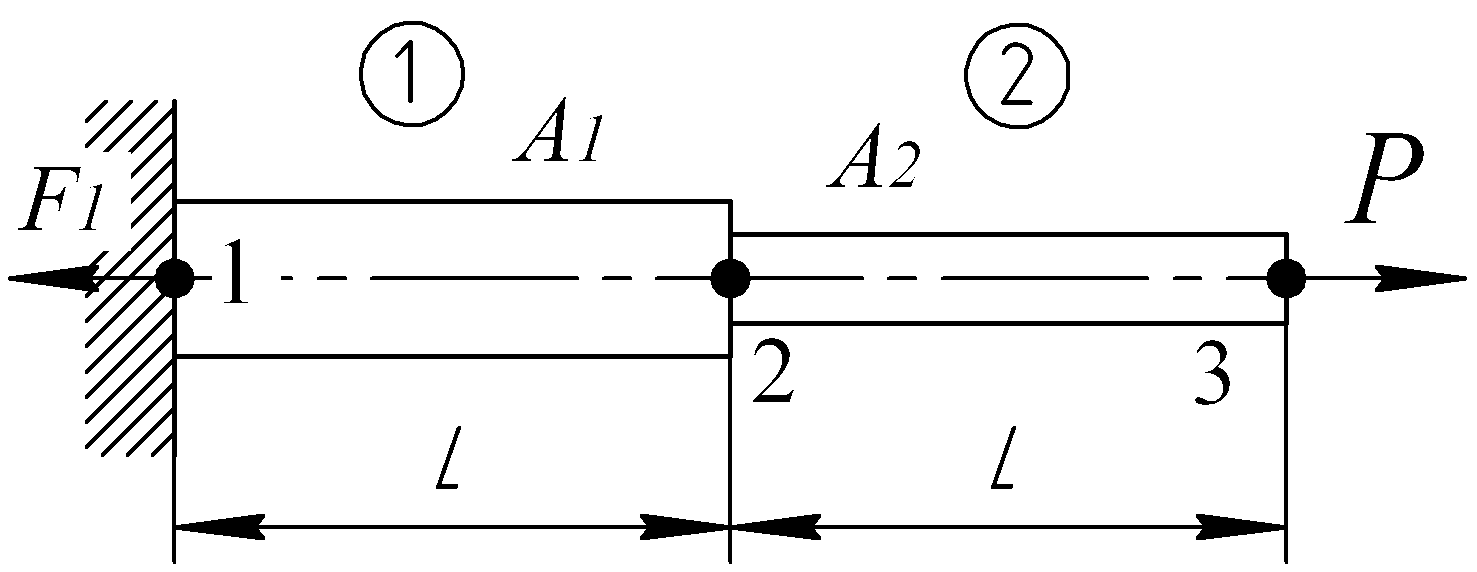
Рис. 6.36

Учтем следующие граничные условия: в узле 3 приложено усилие Р, в узле 1 действует реакция опоры F₁, узел 2 свободен от внешних нагрузок, смещение в узле 1 u₁=0. После подстановки соответствующих значений в (6.2) получим матричное равенство:

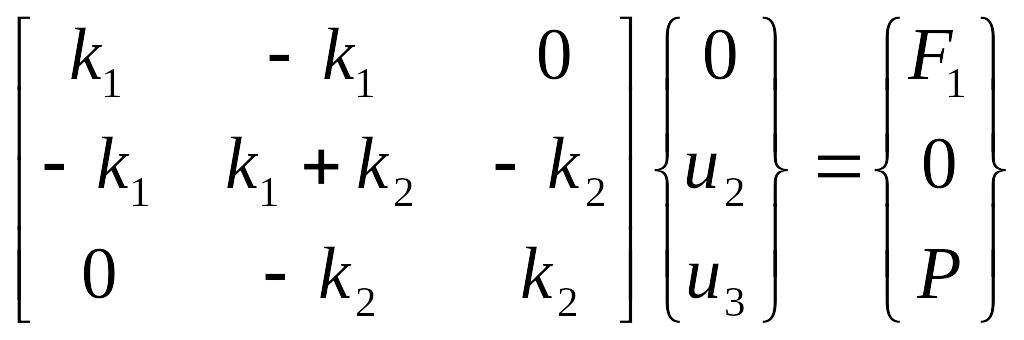(6.3)

или

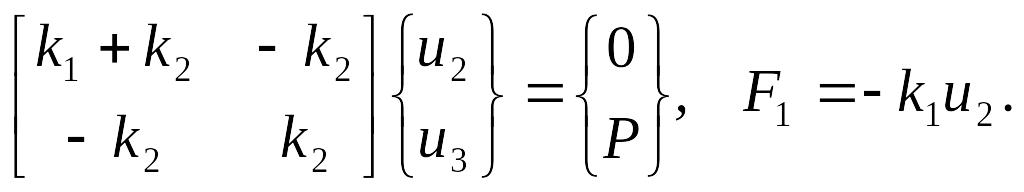(6.4)

Решение матричного уравнения (2.3) дает:

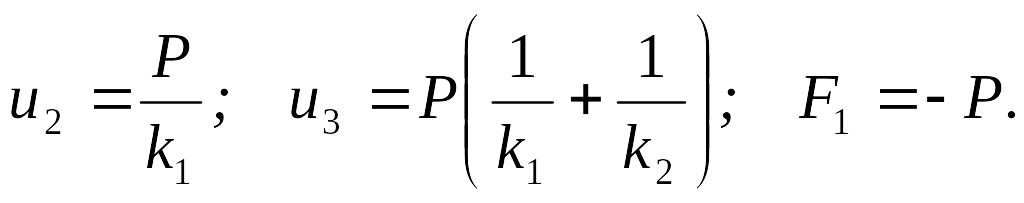
В принятых здесь обозначениях это совпадает с решением методами сопротивления материалов.

6.4.3. Стержневой элемент

Рассмотрим стержень постоянного сечения, воспринимающий только осевую нагрузку (рис. 6.37).

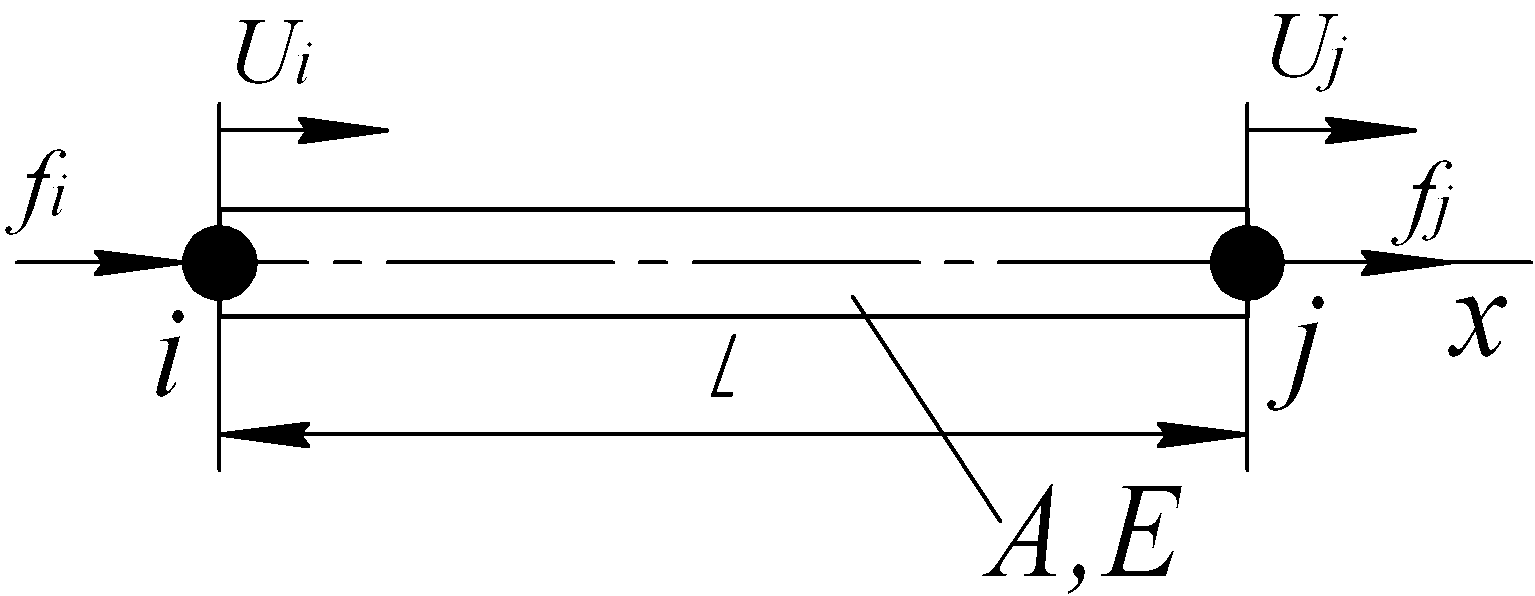
Рис. 6.37

Стержневой элемент характеризуется длиной L, площадью поперечного сечения А и модулем упругости материала Е. Будем, рассматривать зависимости осевых перемещений u = u(х), относительной деформации  = (х) и напряжений =(х) от координаты точки на оси стержня.

Из курса теории упругости известны соотношения между деформациями и перемещениями =du/dx, между деформациями и напряжениями =E.

Рассмотрим построение матрицы жесткости Предположим, что перемещение u изменяется линейно вдоль оси элемента:

. (6.5)

Тогда мы получим:

_, где  - удлинение элемента, (6.6)

=E= E/L. (6.7)

Кроме того, известно:

=F/A. (6.8)

где F - сила, действующая на брус.

Из (2.7) и (2.8) получаем:

F= EA/L=k, (6.9)

где k = EA/L - жесткость бруса, т. е. брус в данном случае работает подобно упругому элементу, и матрица жесткости такого элемента принимает вид:

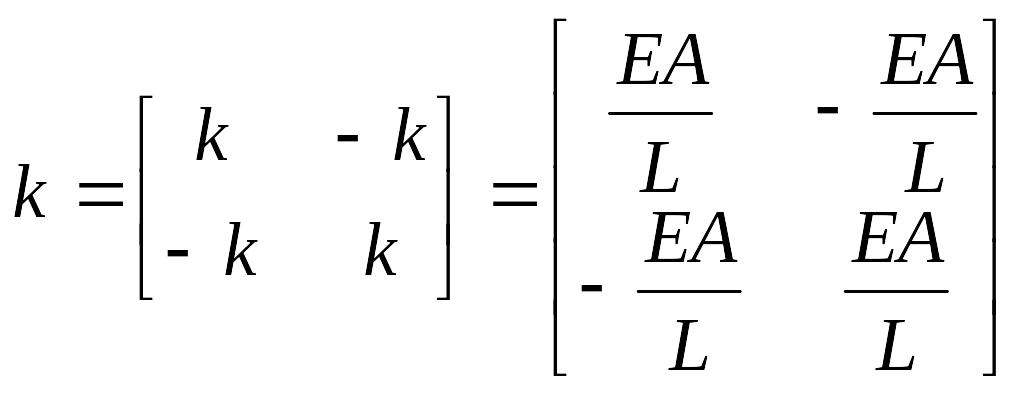, или

Окончательно уравнение равновесия элемента записывается так:

.

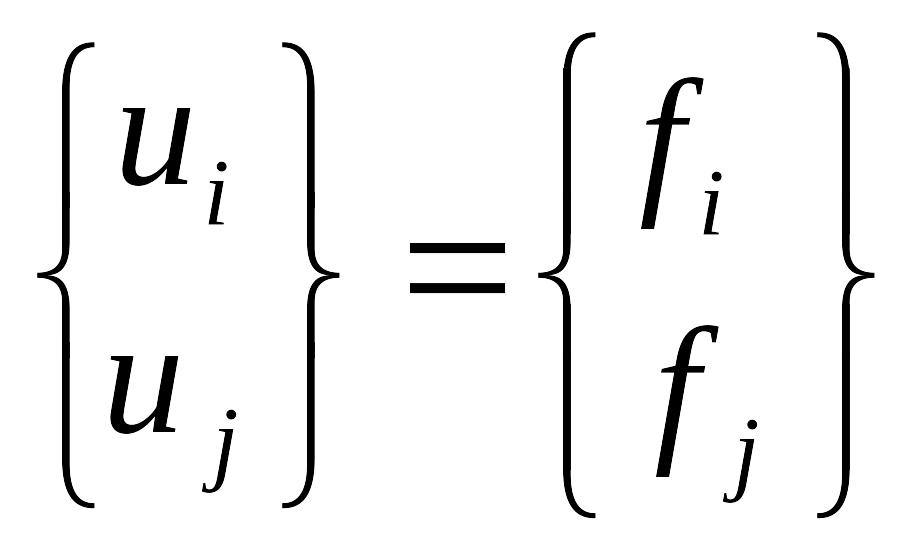Пример 1. Для показанного на схеме ступенчатого бруса, защемленного с торцов и нагруженного силой Р, требуется найти напряжения на каждом из участков.

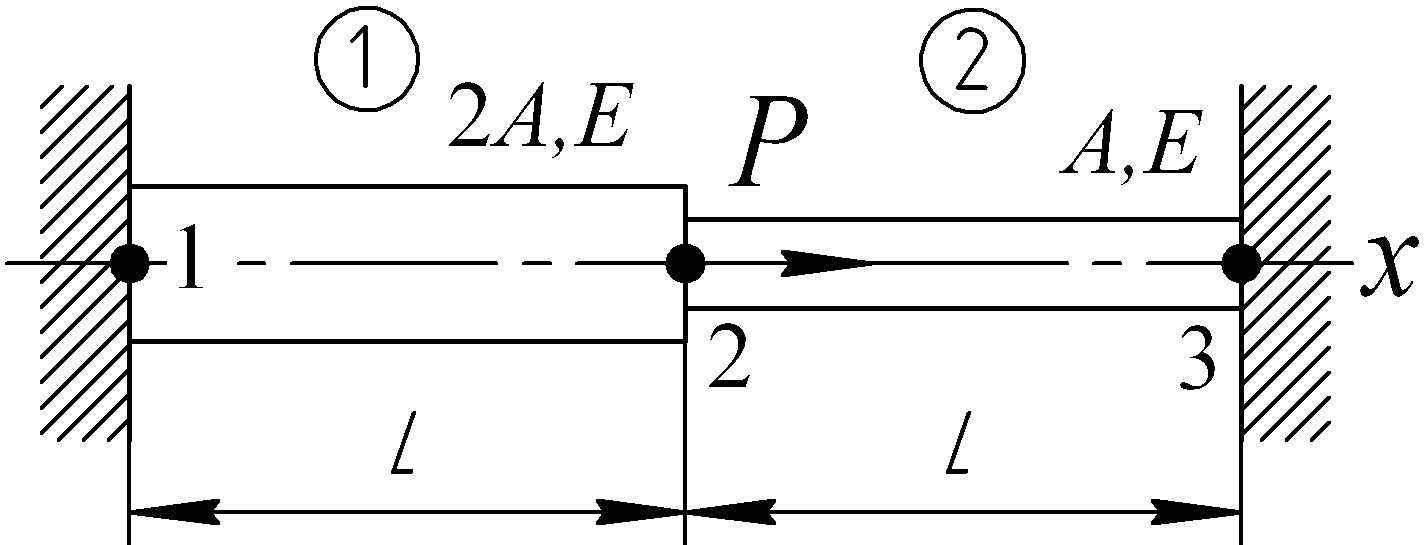
Рис. 6.38

Решение. Показанный на рисунке ступенчатый брус моделируем двумя линейными балочными элементами 1-2 и 2-3. Запишем выражения для матриц жесткости обоих элементов:

u₁ u₂ u₂ u₃

Используя описанный выше принцип суперпозиции, составляем глобальную матрицу жесткости двух последовательно соединенных элементов и записываем уравнение равновесия ступенчатого бруса:

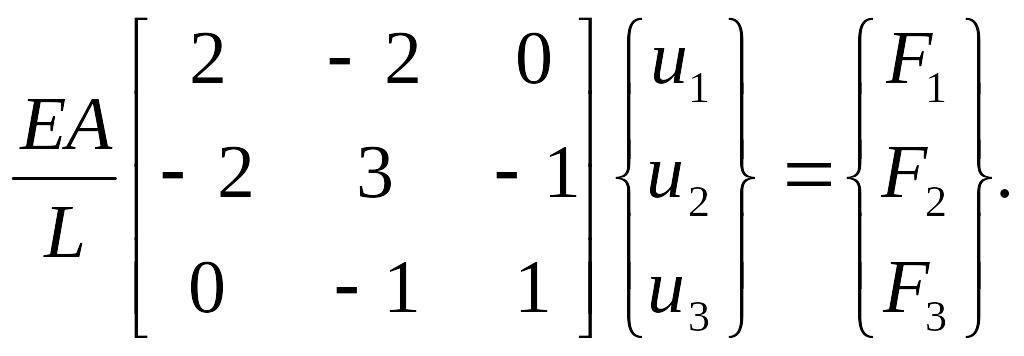
Теперь необходимо приложить нагрузки (в узле 2 приложена заданная сила Р, а в узлах 1 и 3 - реакции опор F₁ и F₃) и учесть граничные условия (u₁=u₃ =0). Тогда уравнение равновесия в матричной форме запишется следующим образом:

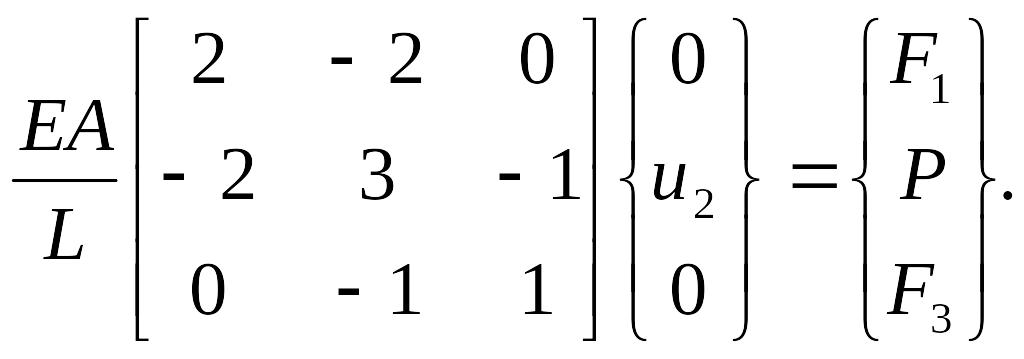
Вычеркивая первые и третьи строки и столбцы, получаем:

.

Таким образом

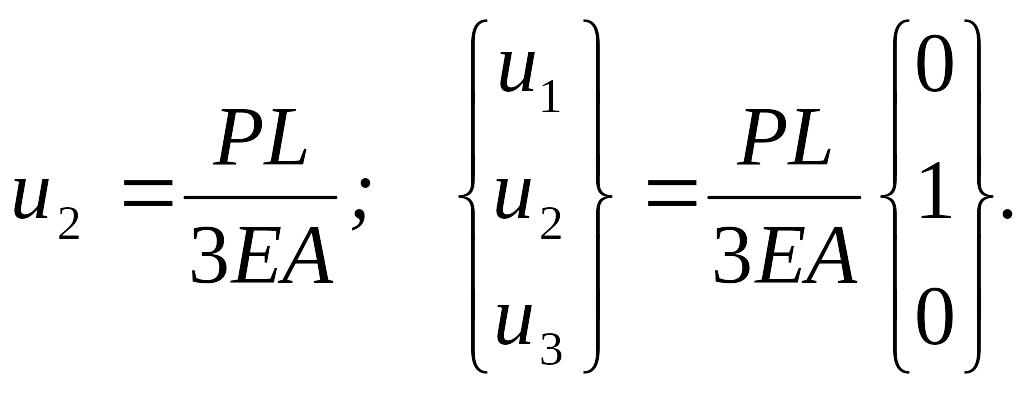
Напряжения в элементе 1 определяются как:

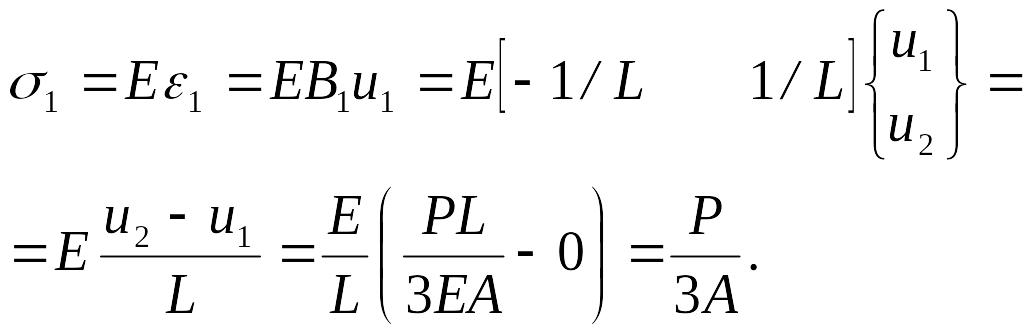
Напряжения в элементе 2

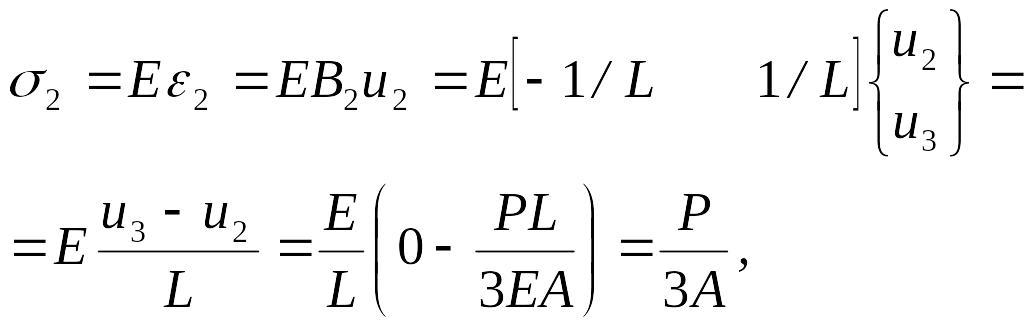
т.е. брус 2 работает на сжатие.

6.4.4. Балочный элемент. Матрица жесткости

Для моделирования упругих одномерных элементов конструкций, несущих изгибную нагрузку (балки), используют балочный элемент. Характеристиками этого типа конечных элементов являются длина элемента L, момент инерции площади поперечного сечения I и модуль упругости Е. Линейный балочный элемент, схематично показанный на рис. 6.39, ограничен двумя узлами i и j, каждый из которых имеет, как минимум, две степени свободы: прогиб  и угол поворота сечения относительно оси Z  = d/dx. В узлах действуют перерезывающая сила F и изгибающий момент M относительно оси Z.

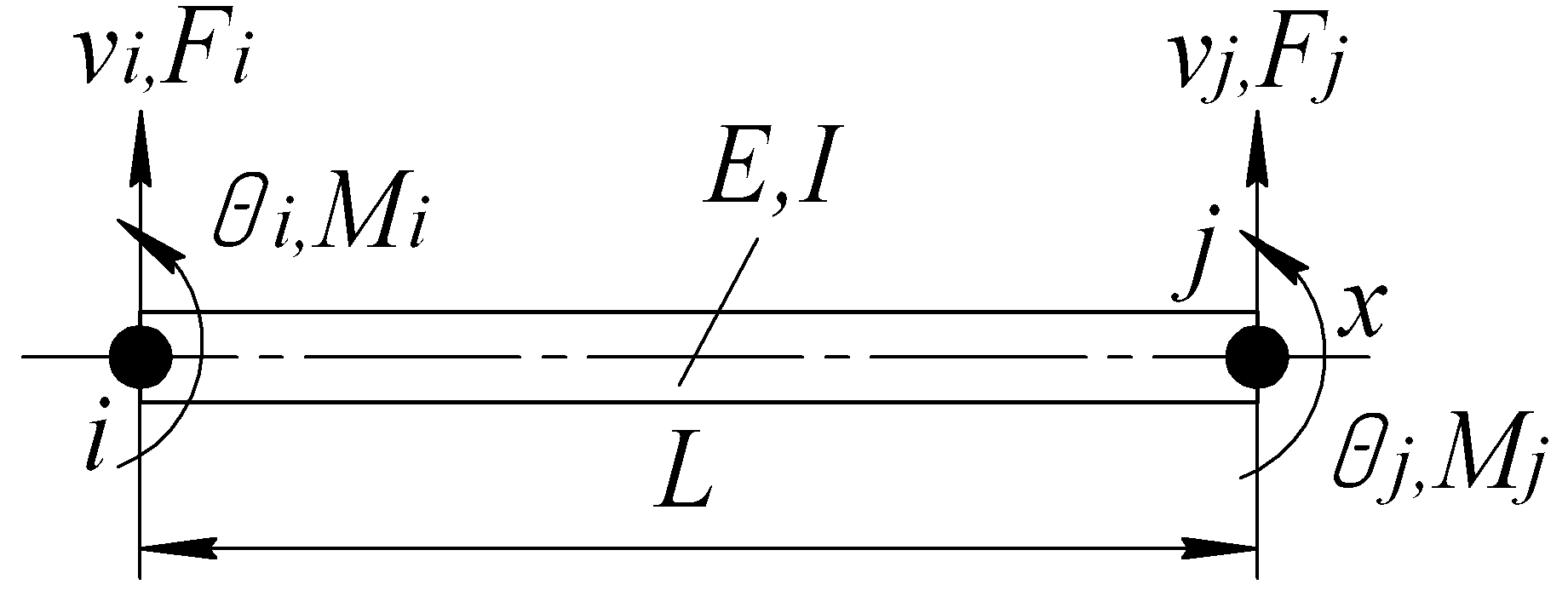
Рис.6.39

Согласно элементарной теории изгиба:

Согласно теории балок, коэффициенты матрицы жесткости в системе координат х, у для элемента с узлами i, j (рис. 6.39):

_i _i _j _j

. (6.10)

Реальные балки воспринимают не только сдвиговые нагрузки и изгиб, но и осевые нагрузки. Матрицу жесткости для балочного элемента в этом общем случае получим комбинированием матрицы жесткости (6.10) с матрицей жесткости для стержневого элемента:

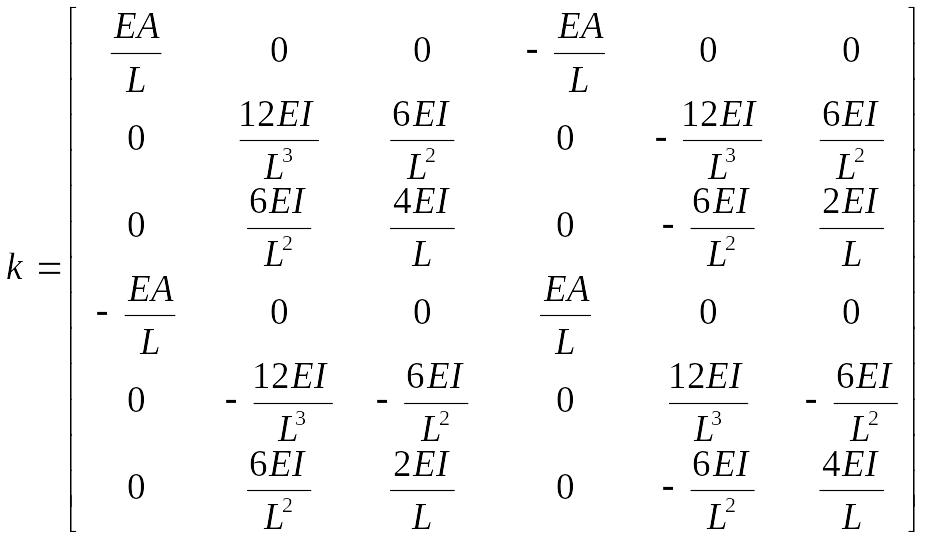
Обратим внимание на то, что элементы матрицы k имеют различные размерности. Это связано с тем, что и компоненты векторов перемещений, и компоненты сил также имеют различные размерности ([м], [рад] и [H], [Нм] соответственно).

Для вычисления матрицы жесткости в пространственной системе координат она записывается сначала в плоской локальной системе координат, а затем переводится в глобальную пространственную систему координат.

Рассмотрим несколько примеров.

Пример 1. Брус (рис. 6.40) защемлен с двух концов и нагружен посредине сосредоточенной силой Р и изгибающим моментом М. Определить смещение и угол поворота узла 2, а также опорные реакции.

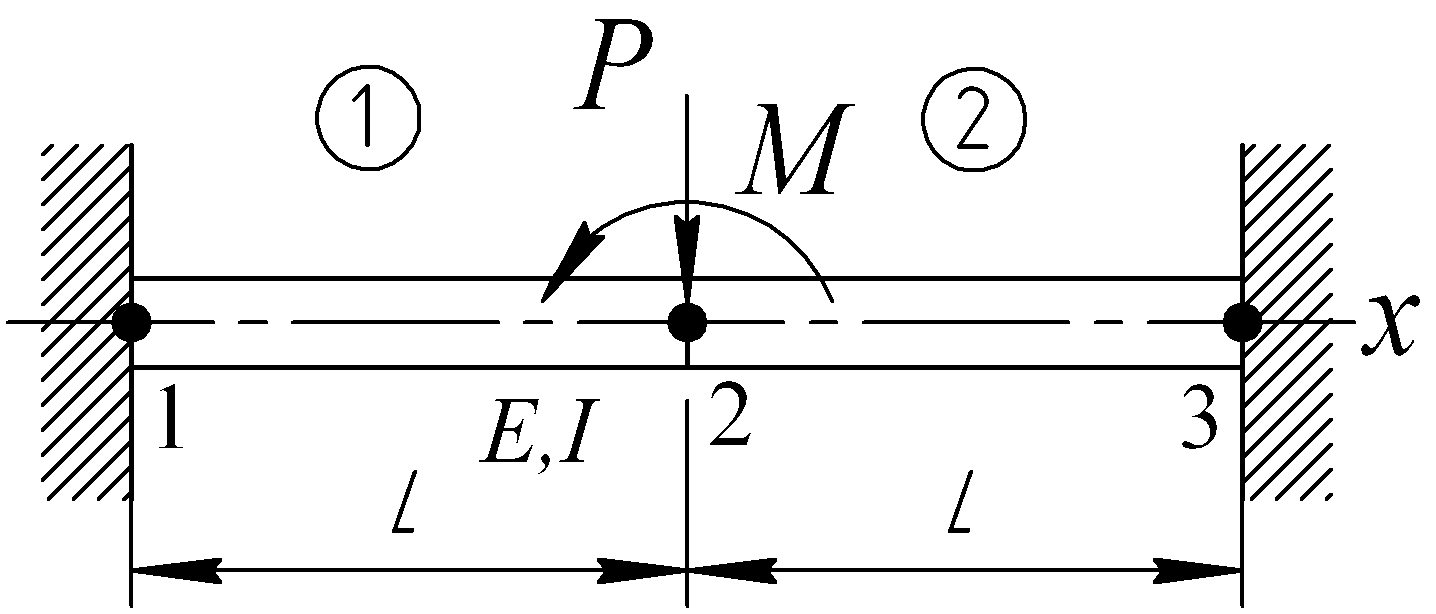
Рис. 6.40

Решение. Сформируем матрицы жесткости отдельных элементов:

₁ ₁ ₂ ₂ ₂ ₂ ₃ ₃

; .

Записываем глобальное конечно-элементное уравнение

₁ ₁ ₂ ₂ ₃ ₃

.

Задаем граничные условия

₁ = ₃ = 0; ₁ = ₃ = 0; F_2Y= -P; M₂ = M.

С их учетом глобальное конечно-элементное уравнение в матричной форме будет выглядеть следующим образом:

.

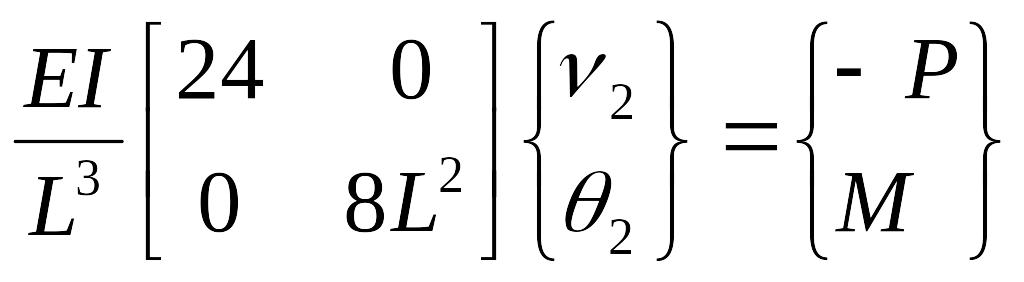Решением этого уравнения является:

.

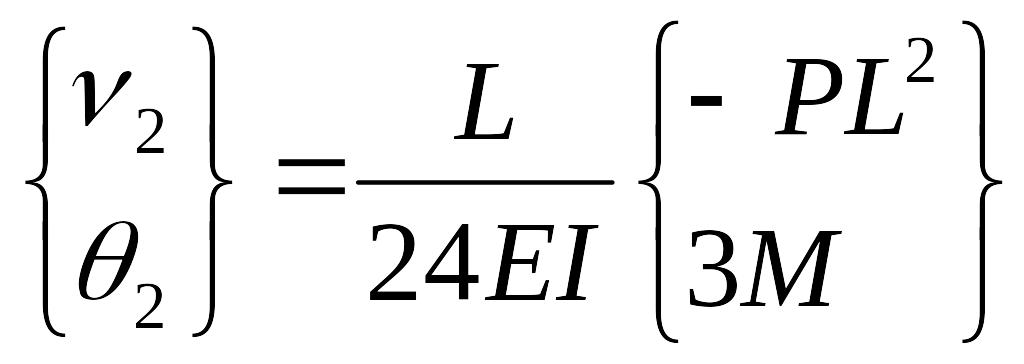Из глобального конечно-элементного уравнения получаем формулы для реакций опор

.

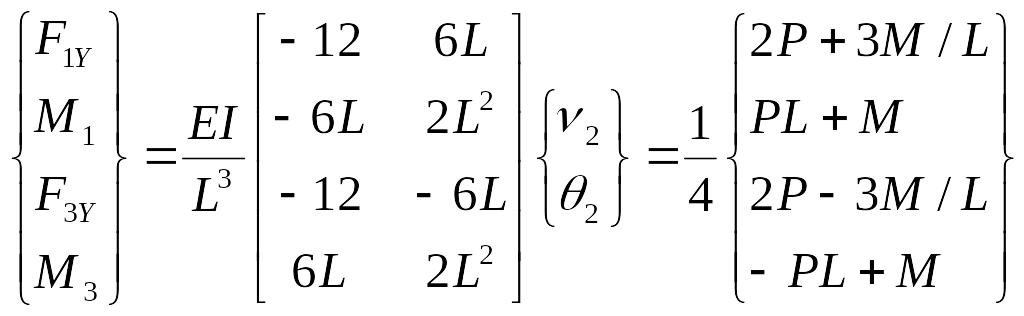Напряжения на концах бруса можно вычислить по формуле

 = _х = -M_y/I.

Пример 2. Дана консольная балка, нагруженная поперечной равномерно распределенной нагрузкой q (рис. 6.41). Определить смещение и угол поворо­та правого конца балки, а также реакции опоры.

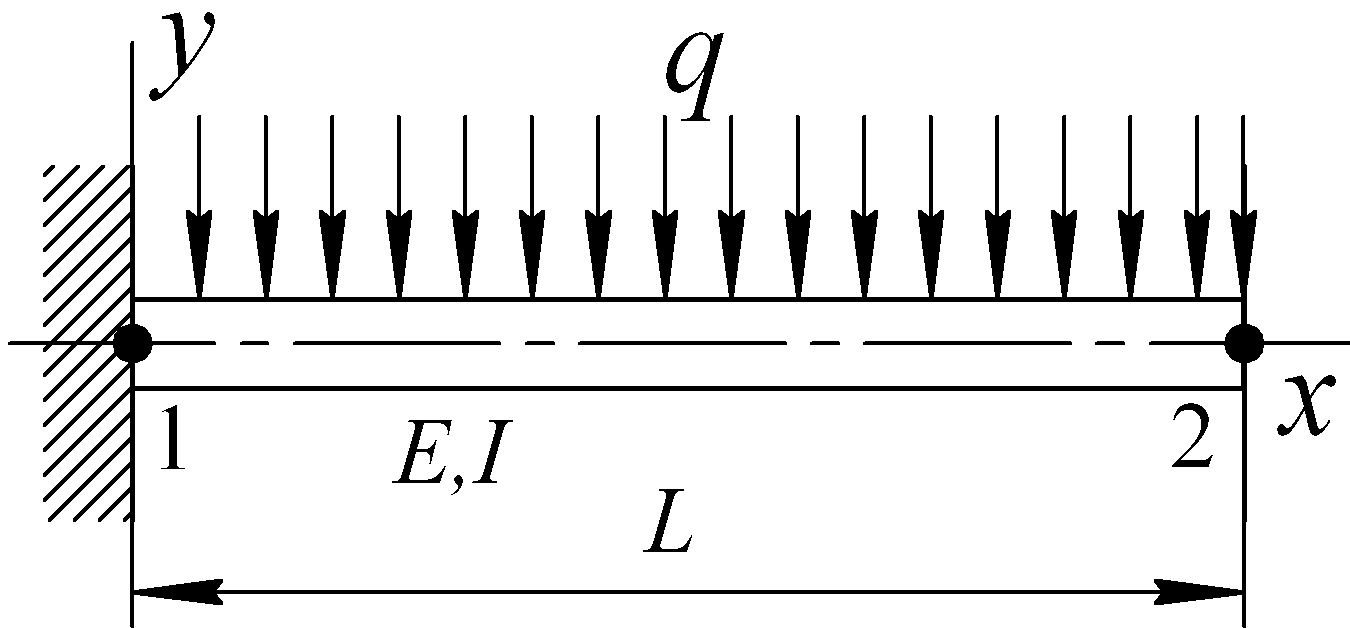
Рис. 6.41

Решение. Сначала рассмотрим вопрос приведения распределенной нагрузки к узлам. Можно показать, что нагрузка трансформируется к узлам, как показано на рис. 6.42, а. Проверить правильность этой схемы можно, сравнивая величину упругой работы деформации для обеих схем.

Применение этого к данной задаче приводит к расчетной схеме, показанной на рис. 6.42, б. Здесь: f = pL/2, m = pL² /l2.

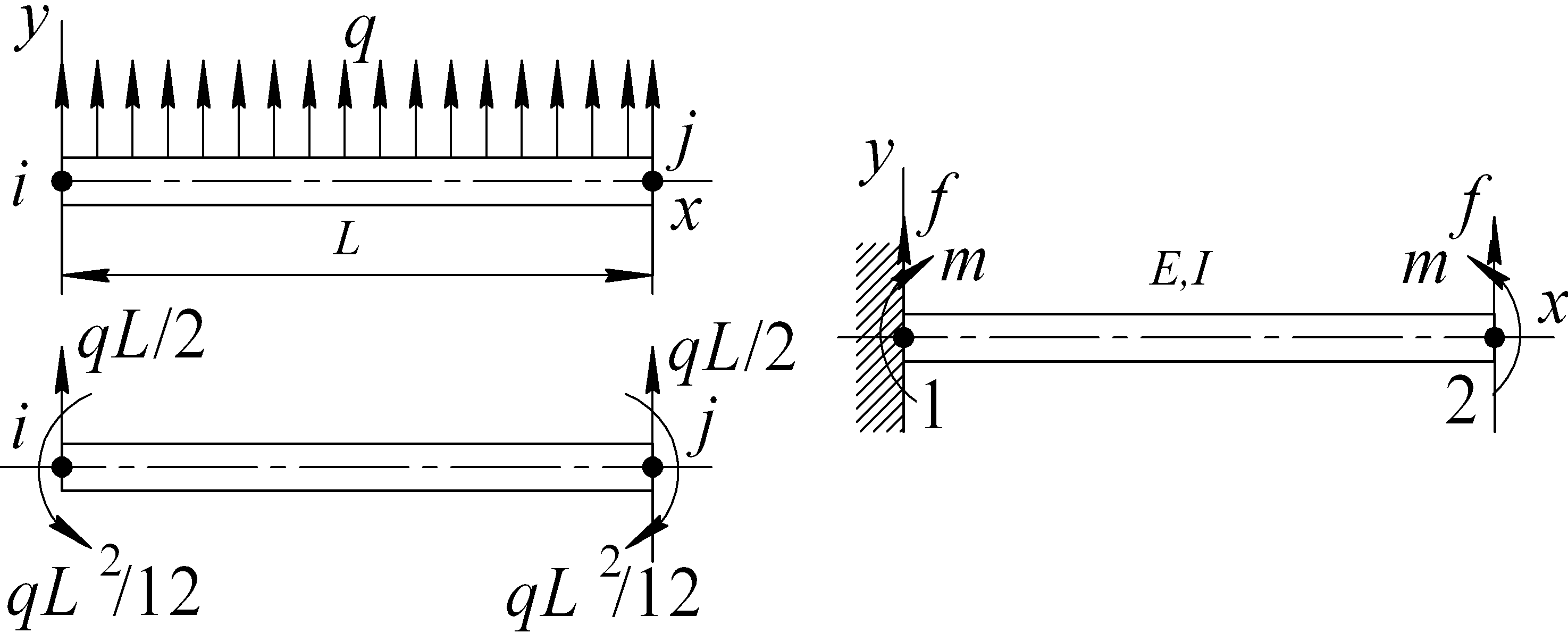
а б

Рис. 6.42

Конечно-элементная система уравнений в матричной форме для данной задачи следующая:

.

Зададим граничные условия: ₁ = ₁ = 0; F_2Y= -f; M₂ = m.

Вычеркивая столбцы и строки с номерами 1 и 2, соответствующие нулевым граничным условиям, получим следующую систему уравнений:

,

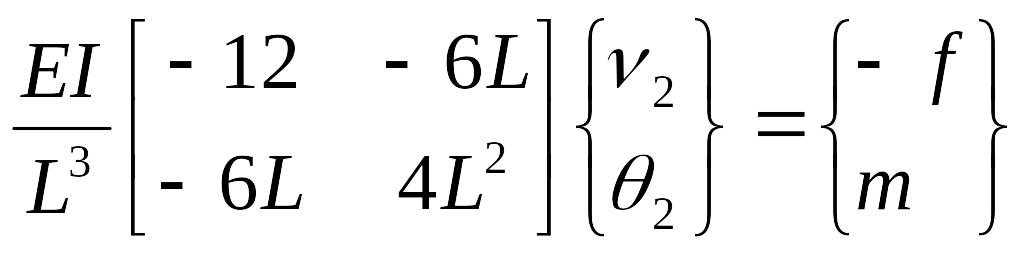откуда находим перемещения правого конца балки:

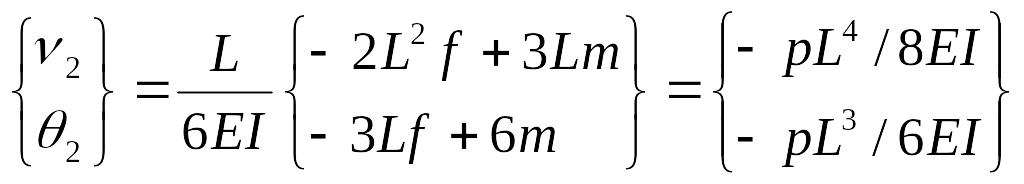. (А)

Из общей системы уравнений равновесия, учитывая (А), получаем реакции опор:

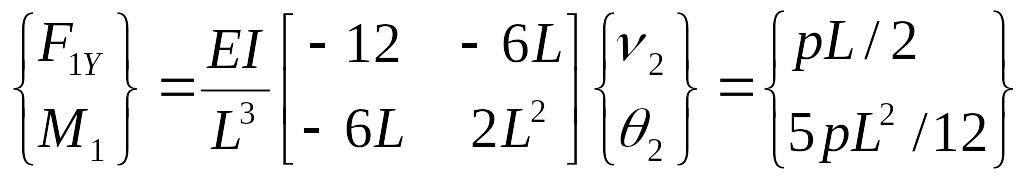. (В)

Заметим, что уравнение (В) представляет собой суммарные силу и момент, действующие на брус в узле 1. Помимо реакций опоры они включают в себя узловые силу и момент, связанные с приведением распределенной нагрузки к узлам. Как видно из рис. 2.12, они составляют:

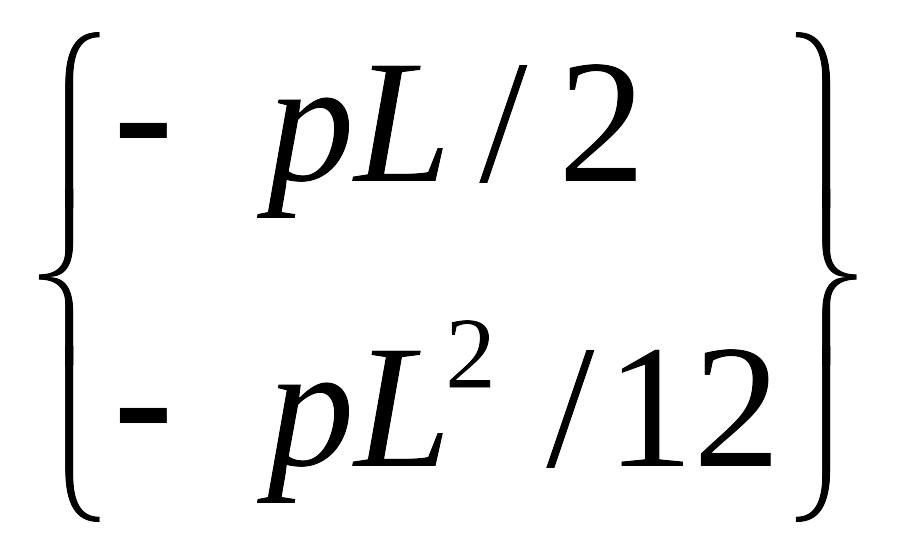
Таким образом, истинные опорные реакции должны быть скорректированы:

.
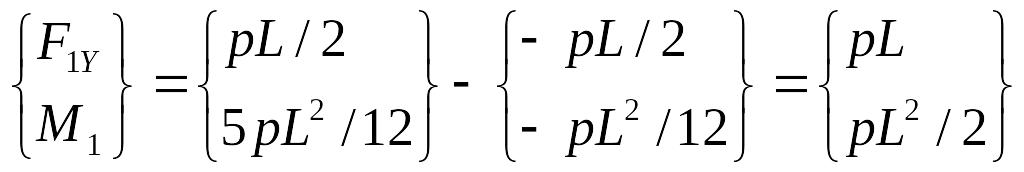