Коэффициент устойчивости

Задача 14. На рис. 14 изображен трактор с навесным рыхлителем. Т — тяговое усилие на гусеничном ходу; и — горизонтальная и вертикальная составляющие результирующей силы рыхления; — сила сопротивления движению самого трактора; — общая сила тяжести трактора с навесным оборудованием; — допустимый (задаваемый) и расчетный коэффициенты устойчивости.

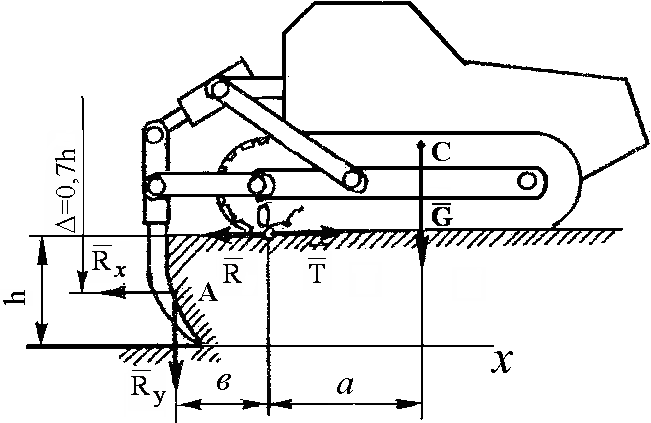
Рис. 14

Требуется объяснить два условия:

, (1)

(2)

РЕШЕНИЕ. Условие (1) есть условие трогания с места вдоль оси и дальнейшего равномерного движения трактора с навесным рыхлителем.

Условие (2) есть соотношение между опрокидывающим моментом силы и восстанавливающим моментом сил и относительно центра О. Расчетный коэффициент устойчивости есть отношение восстанавливающего момента к опрокидывающему и не должен превышать заданного допустимого значения .

Кинематика механизмов

Задача 15. Для измерения малых промежутков времени применяется стробоскоп (рис. 15), основными элементами которого являются два вращающихся соосно диска. Первый имеет радиальных прорезей, второй — сплошной. Если подобрать частоту вращения первого диска такой, что при повороте на угол, равный углу между двумя соседними прорезями , второй диск сделает полное колебание, то проецируемая на него сквозь прорезь стрелка будет казаться неподвижной. Приняв за единицу времени продолжительность поворота диска на угол , определить точность t стробоскопических часов, если , а .

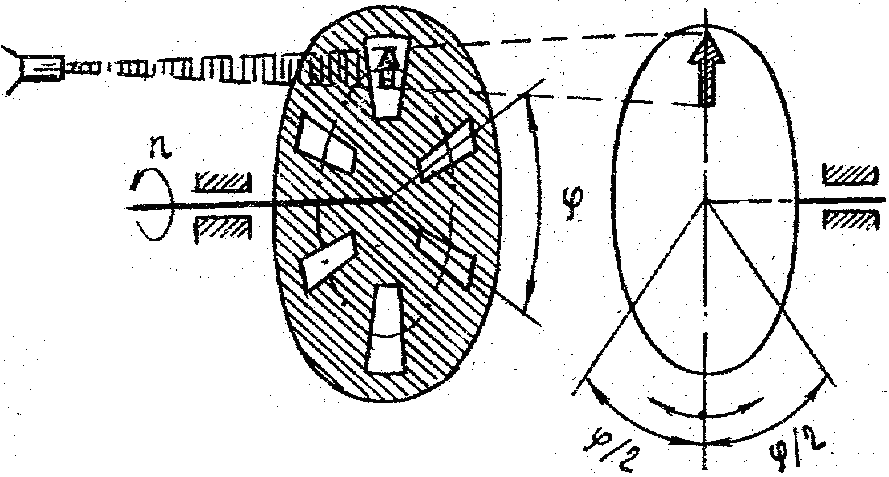
Рис. 15

РЕШЕНИЕ. Точность t есть наименьший промежуток времени, измеряемый с помощью часов. В данном случае t = t,  =  t. С другой стороны, (так устроен первый диск). Так как , то

Задача 16. В вариаторе притирочного станка ведущий вал 1 фрикционной передачи вращается с постоянной угловой скоростью ₁, делая 300 об/мин, и одновременно перемещается в направлений стрелки и обратно согласно уравнению d = (4 + 3cos2t) см. Радиусы дисков r₁ = 5 см, r₂ = 20 см.

Определить угловое ускорение вала 2 как функцию времени; для моментов t₁ = 0, t₂ = 0,25 с, t₃ = 0,5 с определить ускорение точки М на ободе диска 2 (рис.16).

Рис. 16

РЕШЕНИЕ. При отсутствии проскальзывания в точке касания дисков К имеем

Угловое ускорение диска 2 равно

Ускорение точки М

.

Для t₁ = 0 с, t₂ = 0,25 с, t₃ = 0,5 с составим таблицу значений.

t	d, см	, с–1	, с–2	a
t1	7		0	10
t2	4		2	308
t3	1	50 	0	500

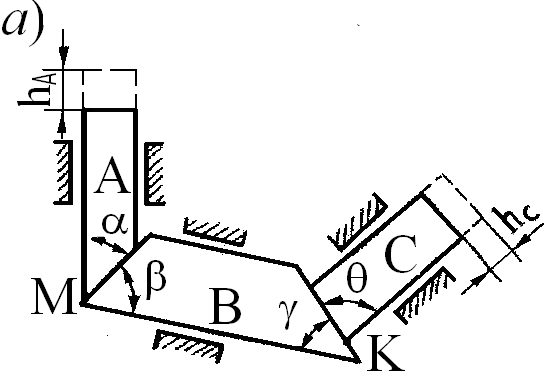
Задача 17. Насколько передвинется ползун С в тройном клине, если ползун А опустился на h_A (рис. 17, а)?

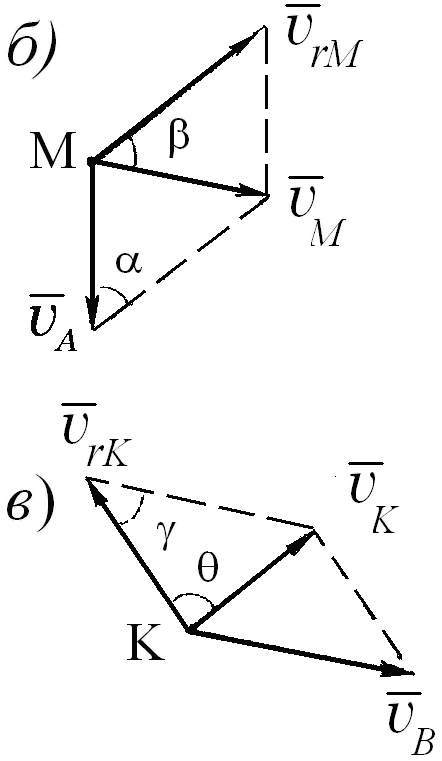
РЕШЕНИЕ. Рассмотрим сложение скоростей (или перемещений) в сложном движении точек М (рис, 17, б) и К

(рис. 17, в).

Абсолютные скорости точек М и К равны:

(1)

(2)

где и — относительные скорости скольжения точек М и К по подвижным поверхностям клина В; и — скорости клиньев А и В относительно их направляющих, т.е. скорости переносного движения для точек М и К соответственно.

Рис. 17. Тонкая подача для изготовления детали

со сложным профилем

По теореме синусов из рис. 17, б и 17, в имеем

(3)

Учитывая, что и и объединяя (1), (2) и (3), окончательно получаем связь между скоростями (перемещениями) ползунов А и С:

Задача 18. Круглый кулачок 1 вращается вокруг оси А с угловой скоростью  = 10 с^–1. Опирающийся на него вертикальный толкатель 2 имеет в верхней части клин, взаимодействующий с подпружиненным горизонтальным ползуном. Определить скорость ползуна 3 для показанного положения механизма (рис. 18, а).

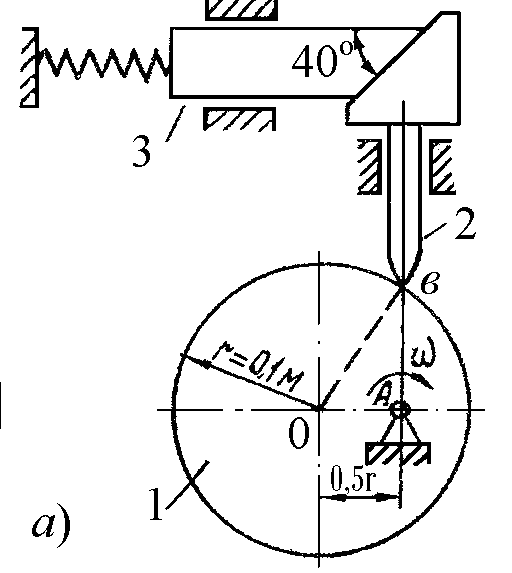
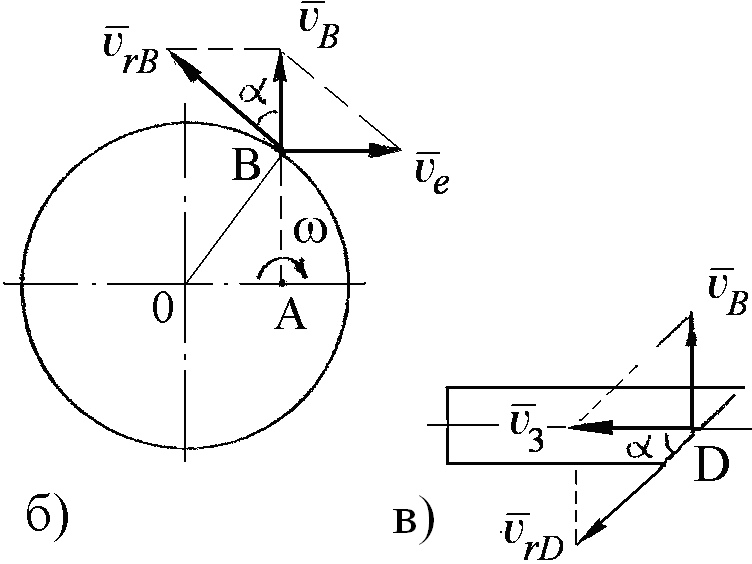
Рис. 18

РЕШЕНИЕ. На основании теоремы о сложении скоростей в сложном движении абсолютная скорость точки В вертикального толкателя равна (рис. 18, б):

где скорость переносного движения =  AB. Из геометрии параллелограмма скоростей имеем

Рассмотрим сложное движение точки D ползуна 3

(рис. l8, в). Для нее движение толкателя 2 со скоростью является переносным движением. Абсолютная скорость точки D, то есть скорость самого ползуна 3, равна:

откуда

Задача 19. В механизме пресса кулачок 1, представляющий собой диск радиусом r = 4 см, вращается с постоянной угловой скоростью  = 0,2 с^–1 вокруг оси, проходящей через точку O перпендикулярно плоскости чертежа, и приводит в движение ползун 2, который скользит в направляющих 3. Для положения, показанного на рис.19,а, определить скорость и ускорение ползуна 2, если ОС = 3 см, а отрезок ОС горизонтален.

РЕШЕНИЕ. Абсолютную скорость точки А ползуна 2 определим как векторную сумму (рис. 19, б)

где — переносная скорость;

Рис. 19

Пo теореме о сложении ускорений в сложном движении точки А имеем (рис. 19, в)

(1)

где

Спроектируем уравнение (1) на ось и получим ускорение ползуна 2

Задача 20. Три конические шестерни 1, 2, 3 (рис. 20, а) находятся в зацеплении. Каково отношение нормальных ускорений точек А и В сцепления шестерен?

Рис. 20

РЕШЕНИЕ. При отсутствии проскальзывания в точке А для линейных скоростей запишем соотношение

(1)

Так как оси вращения шестерен пересекаются в одной точке О, сложим угловые скорости вращения и , направленные по соответствующим осям вращения, и получим мгновенную угловую скорость точки А, участвующей в обоих вращениях (рис,20,б); по теореме синусов имеем

(2)

отсюда с учетом (1) получим

(2)

Отношение нормальных ускорений точки А на шестернях 1 и 2 равно с учетом (1) и (2)

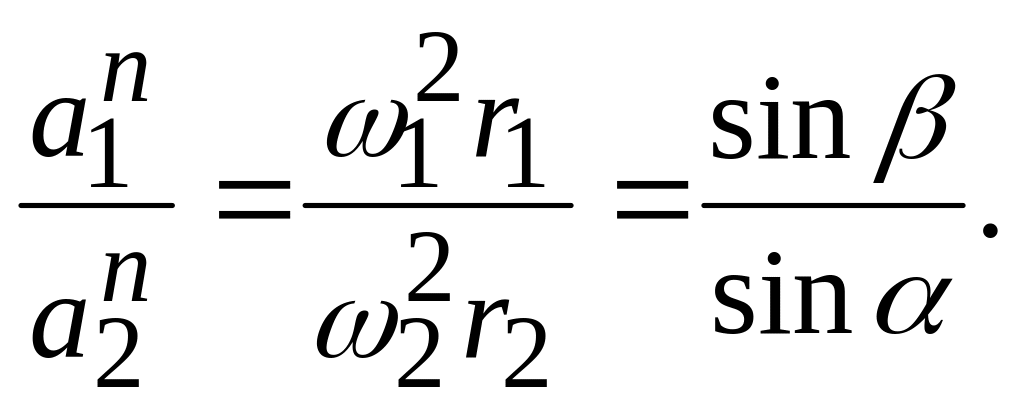
Для точки В из рис.20,в имеем

(3)

Отношение нормальных ускорений точки В на шестернях 1 и 3 равно с учетом (3)

Задача 21. Резец совершает прямолинейное возвратно-поступательное движение, так что его конец М движется по неподвижной оси ОХ по закону x = OM = A sin t. Составить уравнение движения точки М относительно диска 1 (шпинделя), вращающегося равномерно с угловой скоростью вокруг точки О, и найти траекторию этого относительного движения (рис. 21).

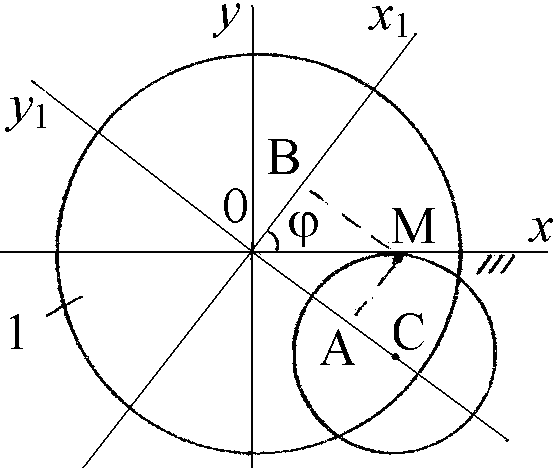
Рис. 21

РЕШЕНИЕ. Выберем подвижную систему координат х₁Oy₁, жестко связанную с диском 1 так, чтобы в начальной момент времени ось Oх₁ совпадала с неподвижной осью Oх. Тогда уравнение переносного вращательного движения будет иметь вид  = t.

Запишем координаты точки М в подвижной системе отсчета:

или

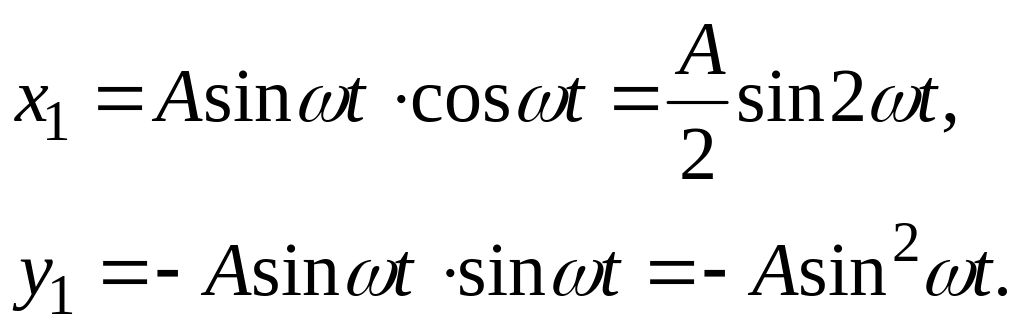
Это и есть уравнения относительного движения резца – относительно тела 1.

Исключаем время t из уравнений движения и получаем уравнение траектории

т.е.

Таким образом, траекторией относительного движения резца (точки М) является окружность с радиусом A/2 и центром в точке с координатами (O; OC = – A/2).

Задача 22. Схват А манипулятора движется по параболе, описываемой уравнениями: x_A(t) = 1,5t м y_A(t) = 0,5t² м. Кривошип OС поворачивается вокруг точки O по закону .

Считая, что в момент времени t = 1 c  = 135^o,  = 90^o, определить в этот момент времени скорость и ускорение шарнира В, а также угловую скорость и угловое ускорение звена АВ, если ОС = СВ = 1 м, АВ =  м.

РЕШЕНИЕ. В момент времени t = 1 с определим проекции скорости схвата А на оси х, y:

Определим скорость точки С:

Рассмотрим плоскопараллельное движение звена ВС

(рис. 22, а):

Рис. 22

или в проекциях на оси х и y имеем:

(1)

(2)

Рассмотрим сложное движения звена ВА (рис. 22, б)

или в проекциях на оси х и y

(3)

(4)

Сравним (1) и (3);

Отсюда следует ; в момент времени t = 1 c .

Сравним (2) и (4);

Определим ускорения.

Из рис. 22, в

или в проекциях на оси x и y

(5)

(6)

Рассмотрим звено ВА (рис. 22, г):

или в проекциях на оси х у.

(7)

(8)

Сравним (5) и (7)

Таким образом,

то есть ускорение точки В направлено по горизонтали в сторону, противоположную положительному направлению оси х.

Задача 23. Волновая передача включает три основных элемента: вращающийся генератор I и зубчатые ― упругий подвижный 2 и жесткий неподвижный 3 венцы. Генератор имеет обкатные ролики 4, которые катятся по внутренней поверхности упругого венца, образуя как бы "бегущую волну", обеспечивающую сцепление обоих венцов. С какой частотой будет вращаться вал венца 2 (необходимые данные указаны на рис. 23) ?

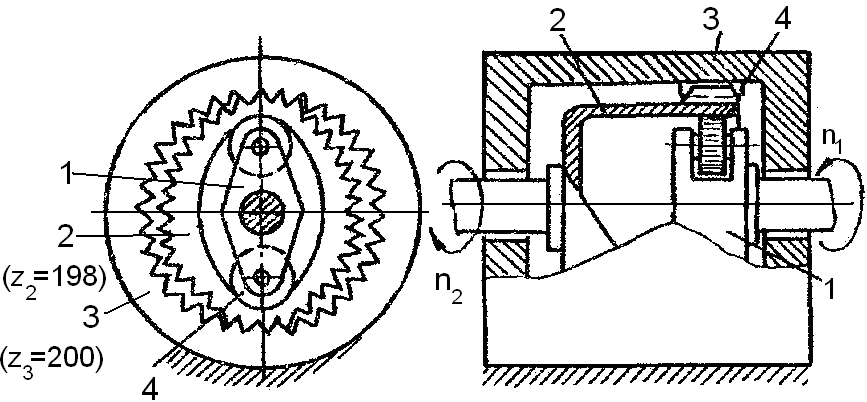
Рис. 23

РЕШЕНИЕ. Применим метод Виллиса. ₁ ― угловая скорость ведущего вала является переносной скоростью для всей системы. Тогда для относительных угловых скоростей ролика 4 и подвижного венца 2 при отсутствии проскальзывания в точках сцепления имеем

(1)

В этих же точках сцепления с неподвижным венцом 3 имеем

(2)

Объединяя (1) и (2), получаем

Так как ₃ = 0;   п, r  z, то последнее соотношение принимает вид откуда

Задача 24. Определить передаточное отношение k₁₂ сферического вариатора в зависимости от угла поворота  промежуточного звена 3.

Известны величины А, r, ,  = 60^o (рис. 15).

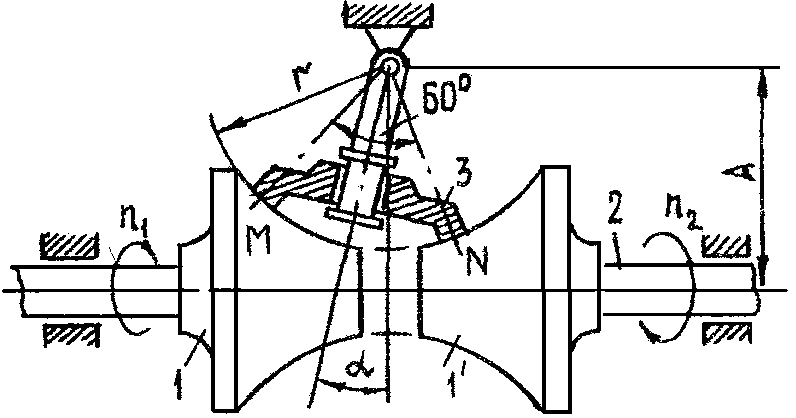
Рис. 24

РЕШЕНИЕ. Для определения передаточного отношения приравняем линейные скорости точек М и N деталей 1, 1' , вращающихся на валах 2, 2.

где п₁, п₂ – число оборотов в минуту валов 1 и 1'. Окончательно получим

Задача 25. В дифференциале зуборезного станка зубчатое колесо 4 сидит свободно на ведущем валу 1. На конце ведущего вала находится головка, несущая ось ab сателлитов 2–2, сцепленных с шестернями 3 и 4.

Определить угловую скорость ведомого вала 5, жестко сцепленного с шестерней 3, если угловая скорость ведущего вала равна ₁, а шестерня 4 вращается с угловой скоростью ₄ в направлении, противоположном вращению вала 1 (рис. 25).

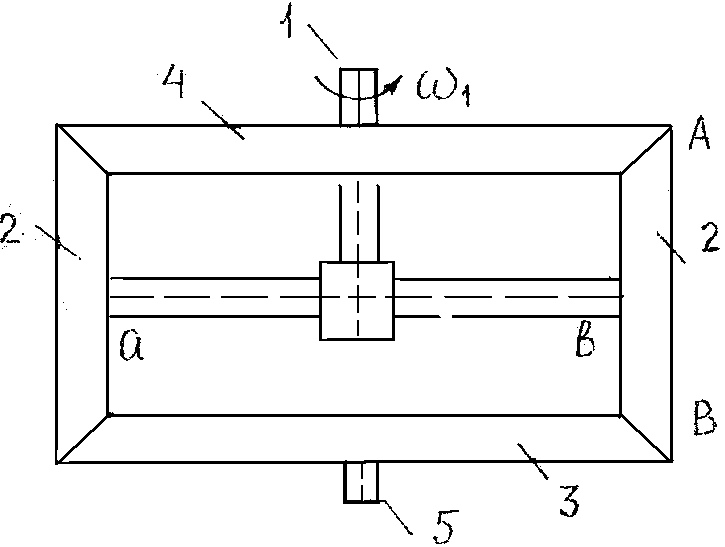
Рис. 25

РЕШЕНИЕ. Механизм имеет две независимые угловые скорости: угловую скорость ₁ ведущего вала и ₄ – угловую скорость свободно сидящей на валу 1 шестерни 4.

Сателлиты 2 совершают сложное движение: вращение вокруг вала 1 с угловой скоростью ₁₂ и вращение вокруг собственной оси ab с угловой скоростью ₁. Если вращение вала 1 происходит против часовой стрелки, то вращение шестерни 4 – по часовой стрелке. С учетом направлений ₁ и ₄ результирующие скорости сложного движения точек зацепления А и В шестерен 2, 4 и 2, 3 соответственно могут быть записаны как алгебраическая сумма скоростей относительного и переносного движений:

(1)

(2)

где по требованиям конструкции

(3)

так как шестерня 5 закреплена на валу 5.

Вычтя из равенства (2) равенство (1), получим с учетом (3) или искомая угловая скорость ₅ ведомого вала равна