Из (I) и (2) получим

или

Так как по условию N₁= 200 G, то можно принять

Окончательно имеем условие работоспособности камнедробилки в виде

Задача 8. Храповое устройство (рис. 8, а) позволяет двигаться направляющей 1 только влево. Считая, что коэффициент трения скольжения между шариком 2 и корпусом 3 значительно больше коэффициента трения скольжения f между шариком и направляющей, определить, при каком угле  храповое устройство работоспособно.

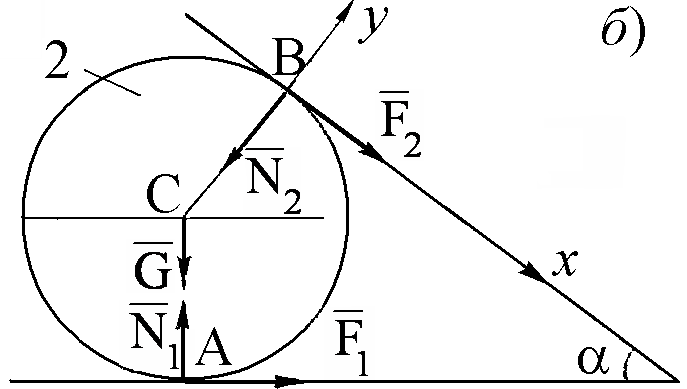
Рис. 8

РЕШЕНИЕ. Рассмотрим равновесие шарика 3 (рис. 8, б) под действием плоской системы произвольно расположенных сил.

Неизвестными являются нормальные реакции N₁, N₂ и угол . Составим три уравнения равновесия:

(1)

(2)

(3)

. (4)

Решая систему уравнений (1 – 4), получаем

или условие работоспособности храпового устройства.

Задача 9. Составить условие работоспособности фрикционного останова одностороннего действия, на тормозном валу 2 которого закреплена муфта 1 с двумя пальцами 3 и объемными кулачками 4, поджатыми к корпусу 6 пружинами 5. При вращении по часовой стрелке кулачки заклиниваются между пальцами и корпусом и вал тормозится. Вращению вала против часовой стрелки ничто не препятствует.

Коэффициент трения между кулачками и корпусом f

(рис. 9, а).

РЕШЕНИЕ. Условие равновесия останова запишем в виде (рис. 9, б)

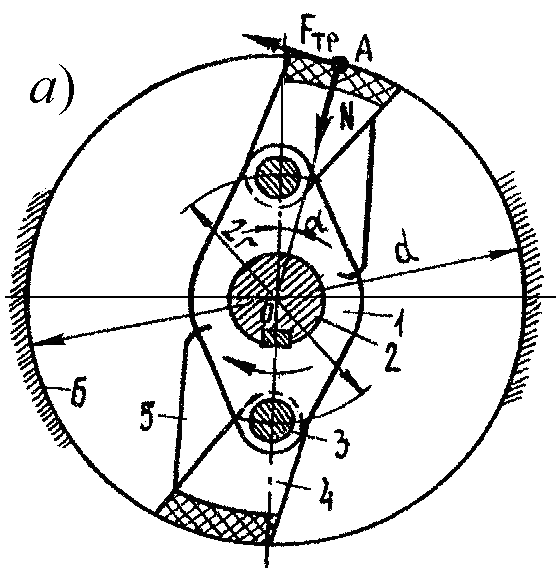
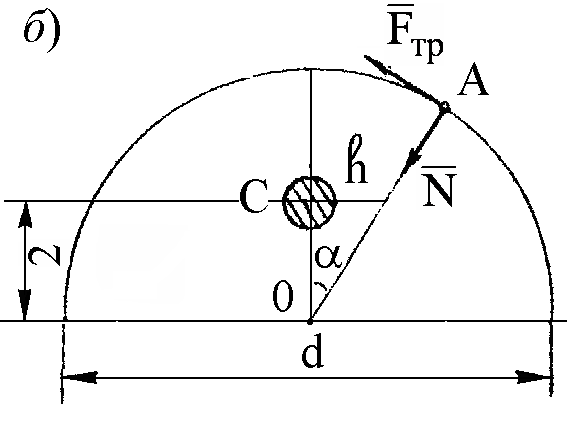
Рис. 9

Окончательное условие работоспособности останова запишется:

или .

Задача 10. Определить максимальный момент М, который может передаваться от диска 1 к кольцу 2 шариковой муфты (рис. 10, а), если между ними имеется восемь шариков 3, прижимаемых пружинами 4 к гнездам диска с силами F = 150 Н. Для предотвращения проворачивания шарики имеют штырьки, на которые одеваются пружинки. Коэффициент трения скольжения между шариками и гнездами диска f = 0,2.

РЕШЕНИЕ. Рассмотрим равновесие шарика 3 (рис. 10, б).

Рассмотрим равновесие диска 1 (рис. 10, в). Так как шариков восемь, то

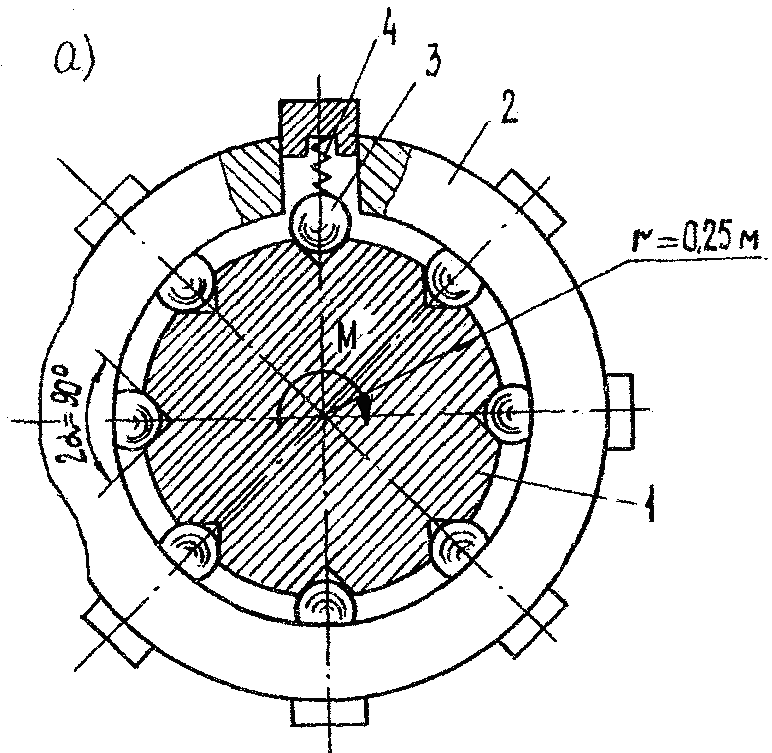
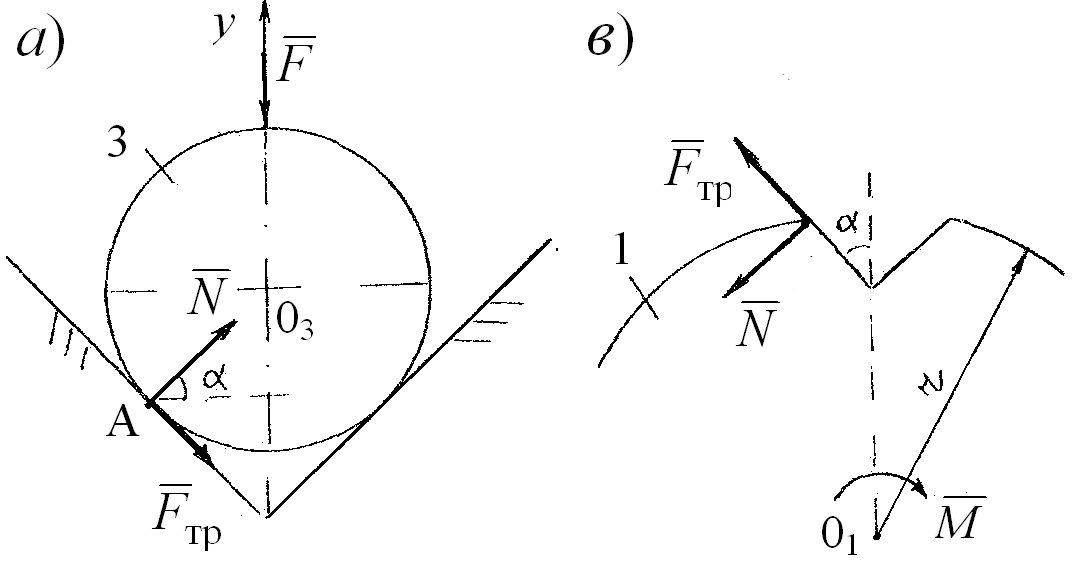
Рис. 10

Подставив (1) в (2), получим искомый максимальный момент

Задача 11. При каком коэффициенте трения скольжения между поднимаемым грузом 1 и захватывающими губками 2 рычагов механизм захвата прутка работоспособен (рис. 11)?

Рис. 11

РЕШЕНИЕ. Составим уравнения равновесия груза 1, учитывая симметрию: (рис. 11, а).

(1)

Составим уравнения равновесия узла О под действием силы и реакций стержней KО и DO, направленных вдоль стержней (R_D = R_K) (рис. 11, б).

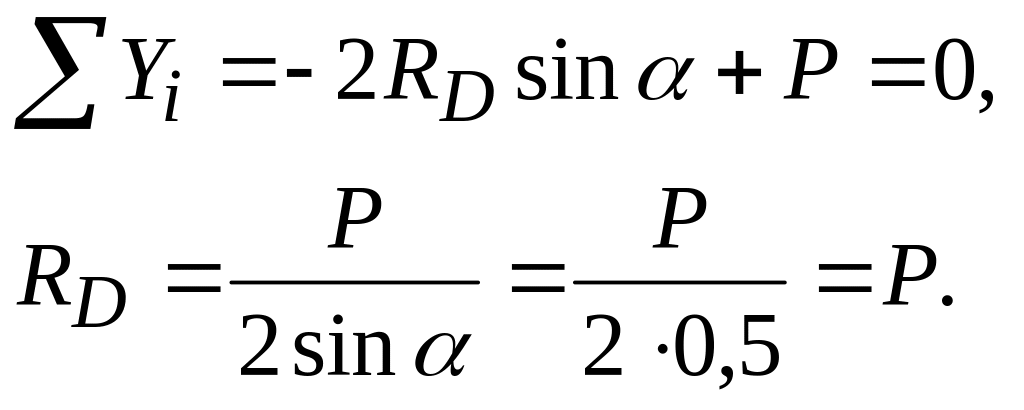(2)

Рассмотрим равновесие захватывающей губки BED

(рис. 11, b)

(3)

(4)

Из (3) с учетом (1) получаем

Из (4) с учетом (2) и последнего равенства имеем

Задача 12. Для перевозки тяжеловесных грузов применяют роликоцепные катки, работающие по принципу гусеницы. Коэффициент трения качения роликов 1 по бетонной поверхности 2 и по опорной плите 3 соответственно ₁ = 0,07 см, ₂ = 0,015 см. Общая вертикальная нагрузка на каток G = 2510⁶ кН. Определить тяговую силу , необходимую для передвижения катка с постоянной скоростью, d = 10 см.

Рис. 12

РЕШЕНИЕ. Из условия равновесия тела 3. (рис. 12, а) определим нормальную реакцию в точке касания А с катком.

Из условия равновесия катка АВ (рис.12, б) определим искомое тяговое усилие

Задача 13. Зубчатая муфта, состоящая из двух полумуфт с поджимающими пружинами, имеет ограничение по максимальному моменту , передаваемому в одну (какую?) сторону. Чему равен этот момент, если сила поджатия пружин N,  = 45°, коэффициент трения на рабочих поверхностях зубьев f (рис. 13, a)?

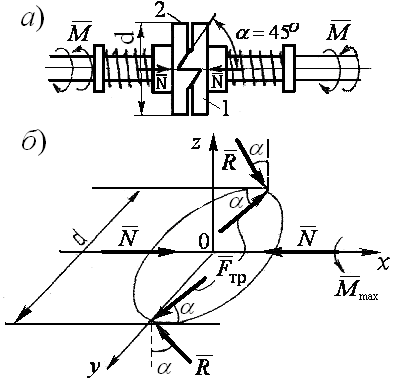
Рис. 13

РЕШЕНИЕ. Рассмотрим рабочую поверхность зуба полумуфты 1 (рис. 13, б). Составим уравнение предельного равновесия полумуфты I под действием максимального передаваемого момента и сил давления со стороны полумуфты 2, нормальной реакции рабочей поверхности зуба и силы трения F_тр = f R.

(1)

(2)

Из (I) имеем

Из (2) получаем величину максимального передаваемого момента

от полумуфты 1 к полумуфте 2.