Равновесие с учетом трения

Задача 6. В пневматических токарных кулачковых патронах применяется самотормозящий клиновой центрирующий механизм [9]. Для заданного угла скоса клина  (рис. 6) и коэффициента трения скольжения f , одинакового на обеих поверхностях клина, установить условия самоторможения и оценить величину запаса самоторможения.

Рис. 6

РЕШЕНИЕ. Рассмотрим находящийся в равновесии односкосый клин с трением на двух поверхностях (рис.6, а). При любом угле скоса  зажатый клин стремится вытолкнуть сила обратного действия , представляющая собой горизонтальную составляющую нормальной реакции – ее вертикальная составляющая. Силе противодействует сила трения на основании клина и горизонтальная составляющая силы трения на наклонной поверхности клина.

Условие равновесия клина

(1)

Из схемы сила трения

(2)

где  – угол скоса клина;  – угол трения. Горизонтальная составляющая силы трения .

Вертикальная составляющая силы трения , равная , суммируется с вертикальной составляющей нормальной силы Соответственно величина нормальной реакции на основании клина

(3)

а сила трения на основании клина

В предельном случае перехода самотормозящего клина в несамотормозящий из (1) имеем

,

При малых углах  произведение близко к нулю, а величина тангенсов углов близка к величине соответствующих углов в радианах.

Тогда условие предельного равновесия клина выразится равенством.

(4)

Полагая углы трения (то есть коэффициенты трения) на обеих поверхностях клина одинаковыми: , получаем

(4′)

Для клина с трением только на наклонной поверхности ( ) условие равновесия будет

Условия (4) и (4') являются условиями самоторможения клина.

Выталкивающая сила (рис. 6, б), необходимая для расклинивания самотормозящего клина, определяется следующим образом.

Заменим силы и равнодействующей и разложим ее на силы и . На основании клина действуют нормальная сила реакции и сила трения . Из условия равновесия клина находим:

Так как из схемы

(5)

то ,

или при

. (6)

Для клина с трением только на наклонной поверхности

.

Сила в формулах (6) и (7) подсчитывается по формуле (3). Для упрощения расчетов можно принимать .

Запас самоторможения k вводится как отношение сил, удерживающих клин в заторможенном состоянии, к силе обратного действия:

. (8)

Величина k должна быть такова, чтобы полностью исключить возможность потери самоторможения механизмом, работающим в условиях вибрации или нагрузок переменного знака.

Выше найдено, что

С учетом этих соотношений из (8) получим

или при

Для предельного случая перехода самотормозящего клина в не-самотормозящий из (4′) и соответственно .

При

У клина с трением только на наклонной поверхности запас самоторможения в два раза меньше, то есть

(9)

Для предельного случая .

Примечание. В самоторомозящих механизмах, подвергавшихся сотрясениям и не имеющих предохранительных устройств от саморасклинивания или постоянного поджима пневмогидроприводом, рекомендуется брать

Задача 7. В щековой дробилке размалываемый камень попадает между подвижной 1 и неподвижной 2 щеками. Расчетное усилие размалывания N в 150―200 раз больше силы тяжести камня G. Принимая коэффициенты трения на обеих щеках одинаковыми и равными f, показать, что условием работоспособности камнедробилки является 2 f > (1– f ²)tg (рис. 7, а и рис. 7, б).

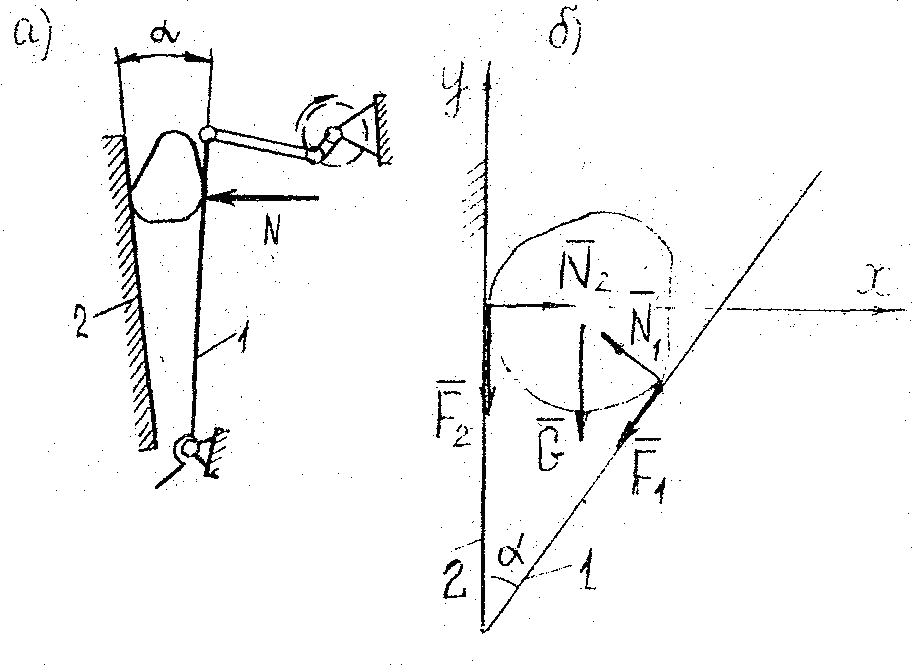
Рис. 7

РЕШЕНИЕ. Рассмотрим равновесие камня под действием плоской системы трех сходящихся сил: (рис. 7, б).

Составим два уравнения равновесия:

(1)

(2)

где