25

ФГБОУ ВПО "Воронежский государственный

технический университет"

Кафедра высшей математики

и физико-математического моделирования

Методические указания

для организации самостоятельной работы по дисциплине «Спецглавы математики», направление подготовки 120301.62 «Приборостроение», профиль «Приборостроение»

очной формы обучения

Воронеж 2015

Составители: канд. физ.-мат. наук Л.Д. Кретова, канд. физ.-мат. наук Н.Б. Ускова

УДК 517.9

Методические указания для организации самостоятельной работы по дисциплине «Спецглавы математики», направление подготовки 120301.62 «Приборостроение», профиль «Приборостроение» очной формы обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. Л.Д. Кретова, Н.Б. Ускова. Воронеж, 2015. 36 с.

Методические указания разработаны с целью организации самостоятельной работы студентов над разделом «Математическая статистика», они также могут использоваться при проведении практических занятий. В начале каждого параграфа разобраны типичные примеры и задачи, далее приводятся индивидуальные варианты задач для самостоятельного решения.

Предназначены для студентов второго курса 4 семестра.

Содержатся в электронном виде в текстовом редакторе Word 2003 в файле спецглавыПС2.doc.

Библиогр.: 3 назв.

Рецензент канд. физ.-мат. наук, доц. Е.Г. Глушко

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

Ó ФГБОУ ВПО "Воронежский государственный технический университет", 2015

При составлении данных методических указаний использовались задачи из [1] – [3].

1. Графическое представление выборки. Статистические оценки параметров распределения

Выборкой объёма n из генеральной совокупности называется последовательность x₁, x₂, …, x_n наблюдаемых значений случайной величины X, соответствующих n независимым повторениям эксперимента. Вариационным рядом выборки x₁, x₂, …, x_n называется способ её записи, при котором элементы упорядочиваются по величичине, т.е. x⁽¹⁾, x⁽²⁾, …, x⁽ⁿ⁾, где x⁽¹⁾ x⁽²⁾ … x⁽ⁿ⁾. Разность между максимальным и минимальным элементами выборки x⁽ⁿ⁾-x⁽¹⁾=w называется размахом выборки. Если в выборке объёма n элемент x_i встречается n_i раз, то число n_i называется частотой элемента x_i, причём . Статистическим рядом выборки называется последовательность пар (x_i, n_i). Статистический ряд записывается в виде таблицы, первая строка которой содержит элементы x_i, а вторая – частоты n_i.

При большом объёме выборки её элементы объединяют в группы, представляя в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки, разбивается на k частично непересекающиеся интервалов. Обычно частичные интервалы имеют одинаковую длину . После того, как частичные интервалы выбраны, определяются частоты n_i^* – количество элементов выборки, попавших в i-тый интервал. Элемент, совпадающий с верхней границей интервала, относят к следующему интервалу. Получающийся статистический ряд в верхней строке содержит середины интервалов группировки x_i^*, а в нижней – частоты n_i^*.

Обычно наряду с частотами n_i^* подсчитывают накопленные частоты , относительные частоты и накопленные относительные частоты . Полученные результаты сводят в таблицу, называемую таблицей частот группированной выборки.

Следует помнить, что группировка выборки вносит погрешность в дальнейшие вычисления, которая растёт с уменьшением числа интервалов.

Полигоном частот группированной выборки называется ломаная с вершинами в точках (x_i^*, n_i^*). Полигоном накопленных частот группированной выборки называется ломаная с вершинами в точках ( ). Полигоном относительных накопленных частот, или кумулятивной кривой, называется ломаная с вершинами в точках ( ).

Гистограммой частот группированной выборки называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группировки так, что площадь каждого прямоугольника равна частоте n_i^* попадания в этот интервал. Отсюда следует, что площадь гистограммы частот равна объёму выборки n. Если длины всех интервалов группировки одинаковы, то высоты прямоугольников считаются по формуле . Аналогично строится гистограмма относительных частот группированной выборки. Высоты прямоугольников в этом случае равны , а площадь равна единице.

Перечисленные выше графические представления выборки аналогично определяются и в случае негруппированной выборки.

Эмпирическая функция распределения F^*(x) определяется по значениям накопленных относительных частот соотношением . Очевидно, что F^*(x) = 0 при x   x⁽¹⁾ и F^*(x) = 1 при x > x⁽ⁿ⁾. На промежутке (x⁽¹⁾, x⁽ⁿ⁾] F^*(x) есть неубывающая кусочно-постоянная функция со скачками в точках x⁽ⁱ⁾.

Аналогично строится F^*(x) по группированной выборке. В этом случае F^*(x) имеет скачки в точках, соответствующих серединам интервалов группировки.

Выборочным средним называется среднее арифметическое элементов выборки:

Если выборка задана статистическим рядом, то:

Для группированной выборки:

.

Рассеивание распределения относительно среднего определяется дисперсией, смещённая оценка которой может быть вычислена по формуле:

;

удобная формула для выборки, представленной статистическим рядом:

.

Несмещенная оценка дисперсии S² связана с формулой:

.

Иногда для упрощения вычислений выборочного среднего и дисперсии, данные группированной выборки преобразуют следующим образом:

где - значение середины интервала x_i^*, встречающиеся с наибольшей частотой. Теперь величина U_i принимает целочисленные значения, для нее считают среднее выборочное и оценку дисперсии. Среднее выборочное _{и дисперсия Sx}² _{исходных данных связаны со средним и дисперсией Su}² _{преобразованных данных следующими формулами:}

;

.

Обратите внимание, что вычислительные формулы для выборочных (эмпирических) начальных и центральных моментов отличаются от известных из теории вероятностей соотношений только тем, что вероятность p_i в последних заменяется на относительную частоту .

Пример 1. Предположим, что имеется партия деталей в 10000 штук. Из этих деталей 9000 годных, а 1000 представляют собой брак. В действительности число годных и негодных деталей неизвестно. Для того чтобы можно было судить хотя бы приблизительно об относительной доле брака, отбирают и контролируют сто деталей. В этом примере генеральной совокупностью является исходная партия деталей в 10 000 штук. Выборкой является множество деталей, изъятых из генеральной совокупности для контроля. Отметим, что описанная процедура назы­вается выборочным контролем качества продукции.

Пример 2. Из партии товара случайным образом выбраны 25 изделий. Их вес (в граммах) оказался следующим: 54; 51; 54; 47; 49; 47; 49; 54; 51; 48; 49; 54; 54; 47; 49; 48; 51; 51; 54; 53; 49; 49; 48; 49; 51. Составить вариационный ряд и статистический ряд, определить размах.

Решение. Вариационный ряд имеет вид: 47; 47; 47; 48; 48; 48; 49; 49; 49; 49; 49; 49; 49; 51; 51; 51; 51; 51; 53; 54; 54; 54; 54; 54; 54.

Размах: w = 54 – 47 = 7.

Статистический ряд представлен в табл. 1.

Таблица 1

xi	47	48	49	51	53	54
ni	3	3	7	5	1	6

Пример 3. Дано следующее время работы некоторого прибора до первого сбоя:

22, 18, 20, 22, 13, 14, 17, 18, 20, 19.

Представить выборку в виде вариационного и статистического ряда. Построить полигон частот, полигон накопленных частот, полигон относительных частот и эмпирическую функцию распределения. Вычислить: , S².

Решение. Вариационным рядом для данной выборки является ряд:

13, 14, 17, 18, 18, 19, 20, 20, 22, 22;

статистический ряд представлен в табл. 2.

Таблица 2

xi	13	14	17	18	19	20	22
ni	1	1	1	2	1	2	2

Объём выборки равен 10, размах w = 22 – 19 = 9. Ниже представлены полигон частот (рис. 1), полигон относительных частот (рис. 2), полигон накопленных частот (рис. 3), полигон относительных накопленных частот (рис. 4), эмпирическая функция распределения (рис. 5).

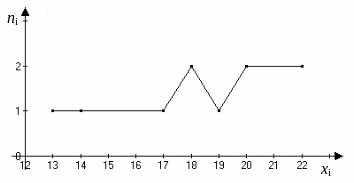
Рис. 1. Полигон частот

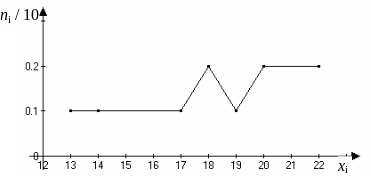
Рис. 2. Полигон относительных частот

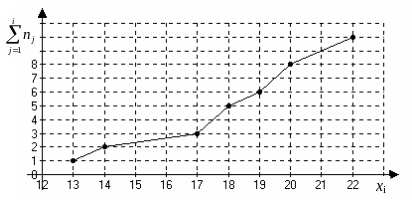
Рис. 3. Полигон накопленных частот

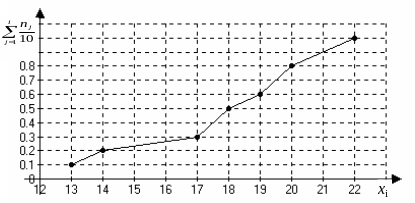
Рис. 4. Полигон относительных накопленных частот

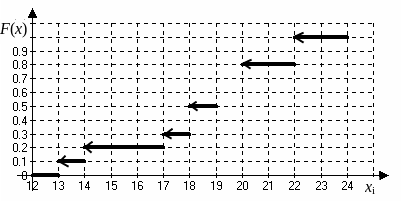
Рис. 5. Эмпирическая функция распределения

Вычисляем теперь и S²:

Пример 4. Время, за которое пассажир прибывает в аэропорт до вылета, случайно, так как зависит от многих факторов. В табл. 3 приведены (в сгруппированном виде) результаты двухсот наблюдений, проведённых в некотором аэропорту. Здесь же приведены результаты вычислений соответствующих частот, относительных частот и накопленных частот.

Таблица 3

№	Границы интервалов	Сере-дины xi*	Час-тота ni*	Накоп-ленная частота	Относи-тельная частота	Относит. накоп-ленная частота
1	[0 – 20)	10	17	17	0,085	0,085
2	[20 – 40)	30	30	47	0,15	0,235
3	[40 – 60)	50	27	74	0,135	0,37
4	[60 – 80)	70	43	117	0,215	0,585
5	[80 – 100)	90	34	151	0,17	0,755
6	[100 – 120)	110	29	180	0,145	0,9
7	[120 – 140)	130	9	189	0,045	0,945
8	[140 – 160)	150	8	197	0,04	0,985
9	[160 – 180)	170	3	200	0,015	1

Пример 5. Представить выборку 55 наблюдений в виде таблицы частот, используя 7 интервалов группировки.

Выборка: 17 19 23 18 21 15 16 13 20 18 15

20 14 20 16 14 20 19 15 19 16 19

15 22 21 12 10 21 18 14 14 17 16

13 19 18 20 24 16 20 19 17 18 18

21 17 19 17 13 17 11 18 19 19 17

Построить полигон и гистограмму частот, полигон относительных накопленных частот и эмпирическую функцию распределения.

Решение. Считаем размах: w = 24 – 10 = 14. Длинна интервала группировки . Результаты группировки сведены в таблицу частот группированной выборки (табл. 4). По результатам группировки строим полигон частот (рис. 6), гистограмму (рис.7), полигон относительных накопленных частот строится аналогично, эмпирическую функцию распределения (рис. 8).

Таблица 4

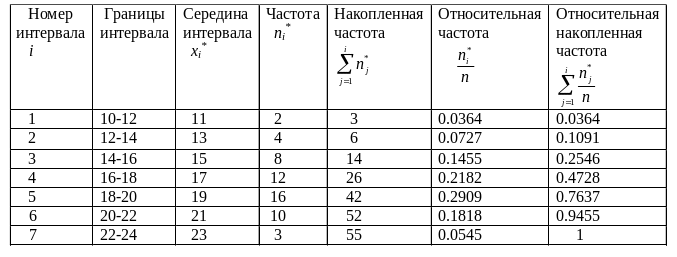
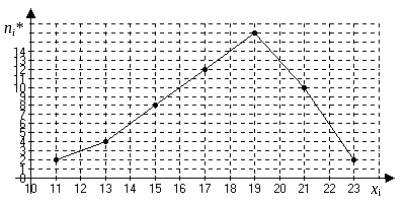
Рис. 6. Полигон частот

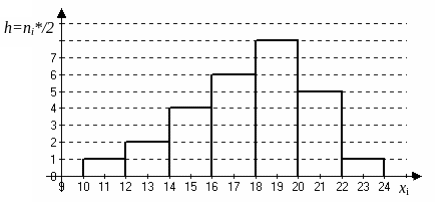
Рис. 7. Гистограмма частот

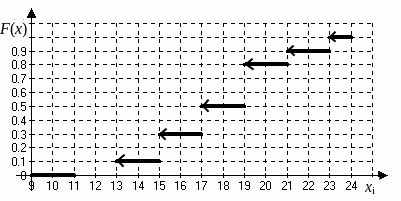
Рис. 8. Эмпирическая функция распределения

Пример 6. Вычислить среднее и дисперсию группированной выборки, представленный в табл. 5.

Таблица 5

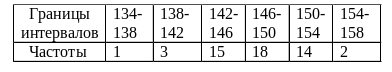
Решение. Длинна интервала группировки b = 4, значение середины интервала, встречающееся с наибольшей частотой, . Таким образом, преобразование последовательности середин интервалов выполняется по формуле:

Вычисления удобно свести в таблицу (табл. 6),

Таблица 6

i	xi*	ui*	ni*	ni*ui	ni*ui2	ni*(ui+1)2
1	136	-3	1	-3	9	4
2	140	-2	3	-6	12	3
3	144	-1	15	-15	15	0
4	148	0	18	0	0	18
5	152	1	14	14	14	15
6	156	2	2	4	8	18
	-	-	53	-6	58	99

последний столбец которой служит для контроля вычислений при помощи тождества:

Подставляя в тождество данные последней строки получим: 58 + 2(–6) + 53 = 99, следовательно, вычисления выполнены верно. Находим:

Переходим обратно от u к x:

.

Пример 7. Измерения ёмкости затвор–сток у 20 полевых транзисторов дали следующие результаты:

1,9; 3,1; 1,3; 1,0; 3,2; 1,1; 2,9; 2,7; 2,7; 4,0; 1,7; 3,3; 0,9; 0,8; 3,1; 1,2; 2,6; 1,9; 2,3; 3,3.

Найти выборочное среднее , выборочную дисперсию и несмещенную дисперсию .

Решение. При большом объеме выборки рекомендуется сначала сгруппировать результаты наблюдений. Это вносит определенную погрешность в дальнейшие вычисления, но существенно их упрощает.

Размах выборки W_x . Разобьем на 8 интервалов, тогда длина каждого интервала будет равна b_x Для вычисления искомых параметров распределения воспользуемся формулами:

₍₂₎

где r – число интервалов, – количество элементов выборки, находящихся в i-м интервале, – середина этого интервала. Промежуточные результаты вьчислений для удобства сведем в таблицу и вычислим сначала и (см. последнюю строку табл. 7).

Таблица 7

Затем по формулам (1) – (3) получаем

Решите примеры 8,9,10 используя данные своего варианта. Исходные данные приведены в Приложении 1, табл. 1, 2, 3.

8. Ошибки измерения при 10 измерениях дальности до цели с помощью радиодальномера приведены в табл. 1. Записать выборку в виде вариационного и статистического ряда, определить ее размах, построить полигон частот и эмпирическую функцию распределения, найти выборочное среднее, несмещенную оценку дисперсии.

9.Частота сигнала собранного радиоэлектронного блока контролируется прибором, не имеющим систематической ошибки. Показатели прибора приведены в табл. 2. Сгруппировать выборку, построить полигон частот, гистограмму, эмпирическую функцию распределения, найти , и .

10. Регистрирующее устройство контроля каждый час фиксирует напряжение в сети. В табл. 3 приведены данные полученные после первичной обработки выборки. Построить гистограмму и найти , и .